webgl进阶之旋转的立方体

与其说是webgl，倒不如说是图形学，毕竟语言只是一个工具。

用过three.js或者其他三维库来开发三维程序的都知道，对于标题所指，其实实现起来很简单，拿three.js来说，一段很简短的代码就能实现：

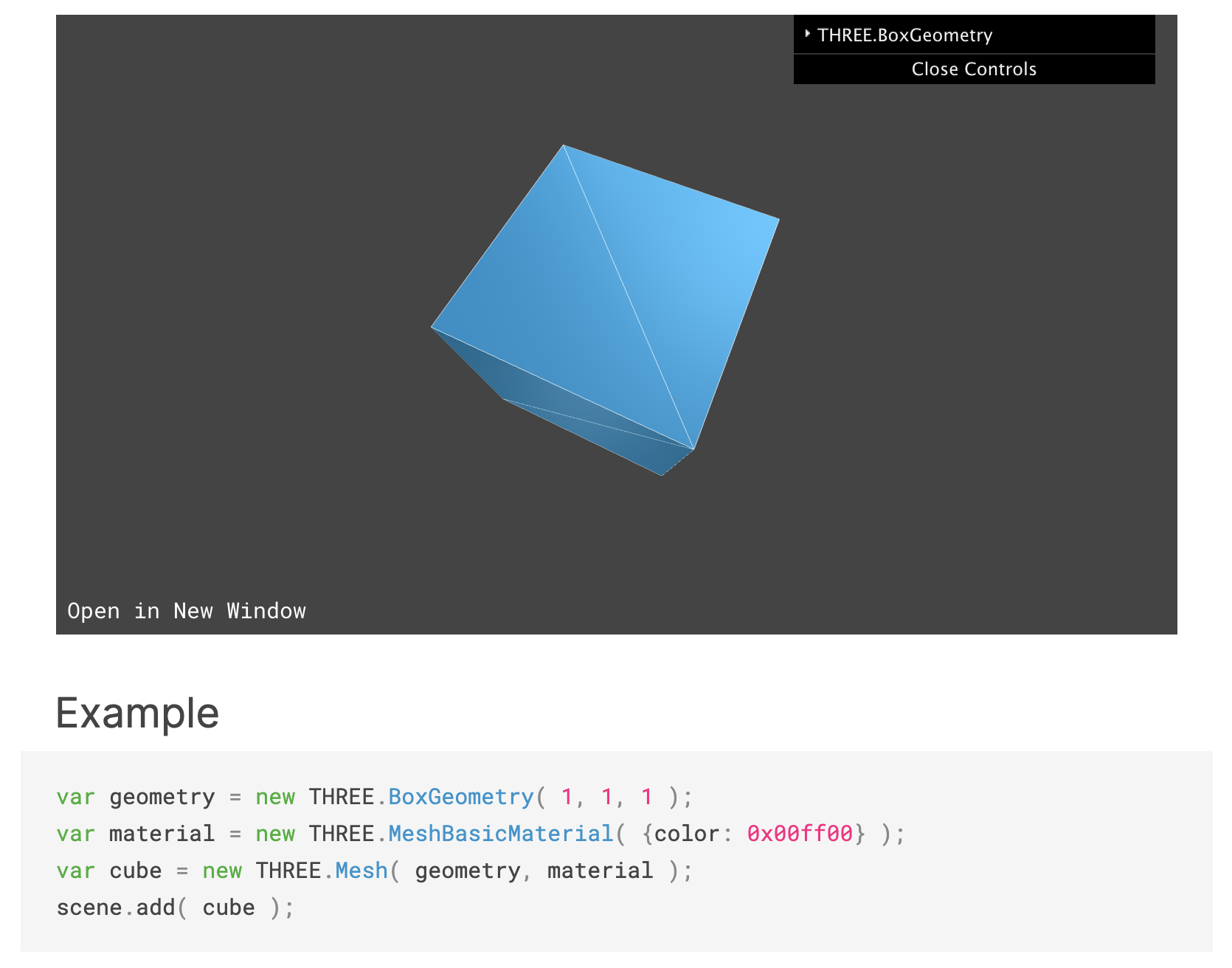
这里也感谢作者和其他开源工作者做出的贡献，因为他们的付出使得我们在web端开发三维程序的门槛大大降低，向大佬们致敬！！！

那么这么一个简单的立方体，究竟是怎样通过webgl实现的呢，今天，我们就来稍加说明一下(默认您已经了解基本的webgl和图形学相关知识，如果没有，请先看完《webgl权威指南》这本书)

1.MVP矩阵

即modelMatrix(模型矩阵)、viewMatrix(视图矩阵)、projMatrix(投影矩阵)

模型矩阵控制模型的旋转、平移；

视图矩阵控制相机相关的参数(position、lookAt、空间坐标系XYZ轴的方向)；

投影矩阵控制三维物体观看的效果(透视相机、正交相机)。

所以一个空间三维几何体，在这些矩阵的共同作用下，就展示在我们面前了

注意:矩阵乘法不满足交换律，所以三个矩阵相乘的顺序不能颠倒

gl.position = projMatrix * viewMatrix * modelMatrix * vec4(a_Position,1.0);

three.js中将模型矩阵和视图矩阵的乘积作为参数传到着色器里，所以我们经常会看到three.js的shader材质中顶点着色器中会有这样固定的一段代码：

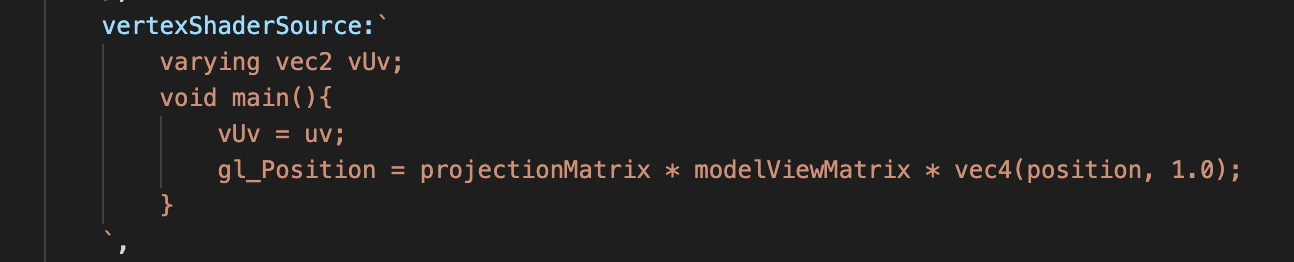
2.构建立方体mesh

我们知道，三维场景中的每个mesh都是按照三角面来绘制的，所以，如果一个立方体长这样的话：

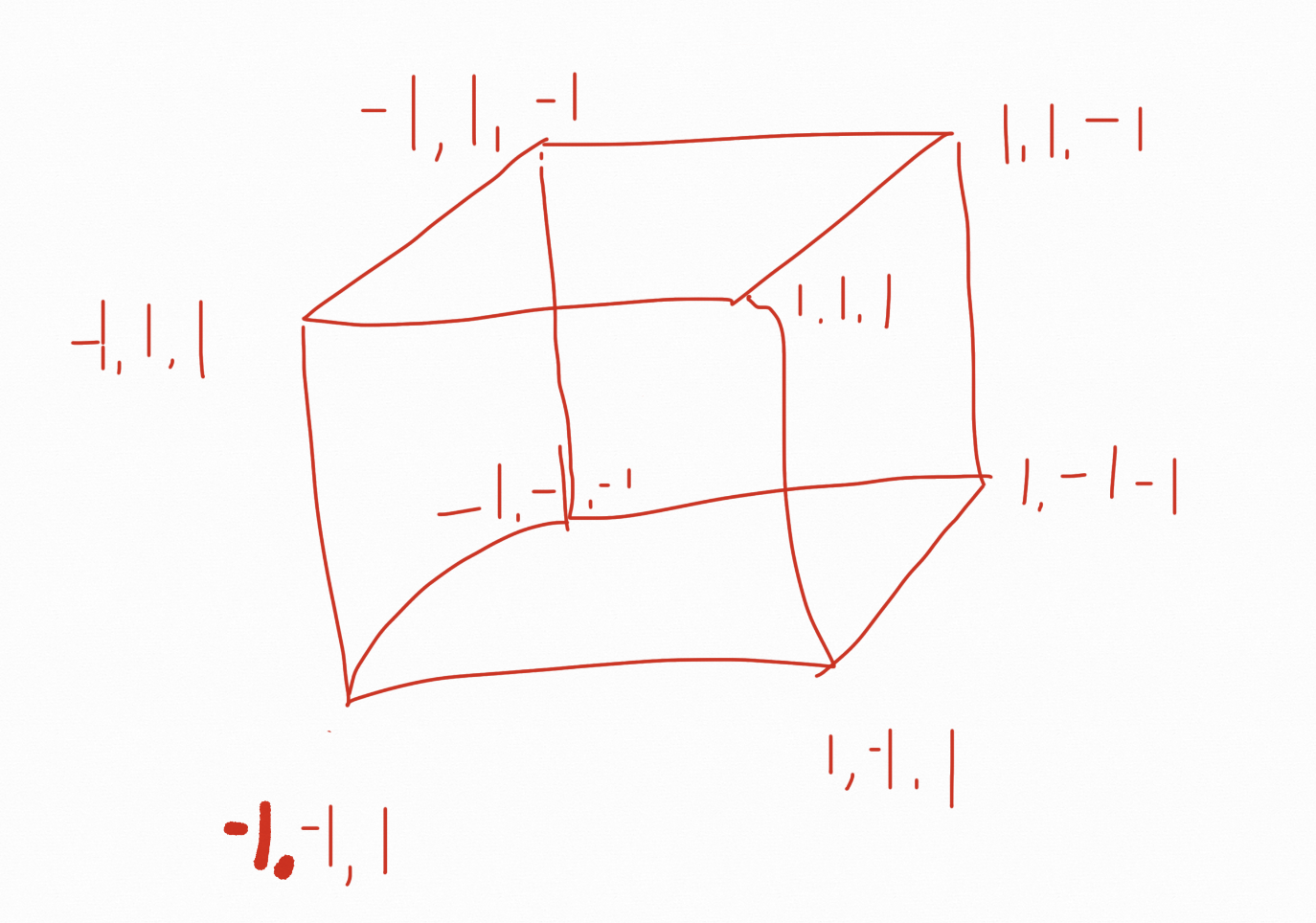
虽然每个面只有4个顶点，但是因为要按照三角面去绘制，那么画一个矩形面要传6个顶点数据

 

正反面区分：

绘制三角形，顶点顺序还是有所讲究的，

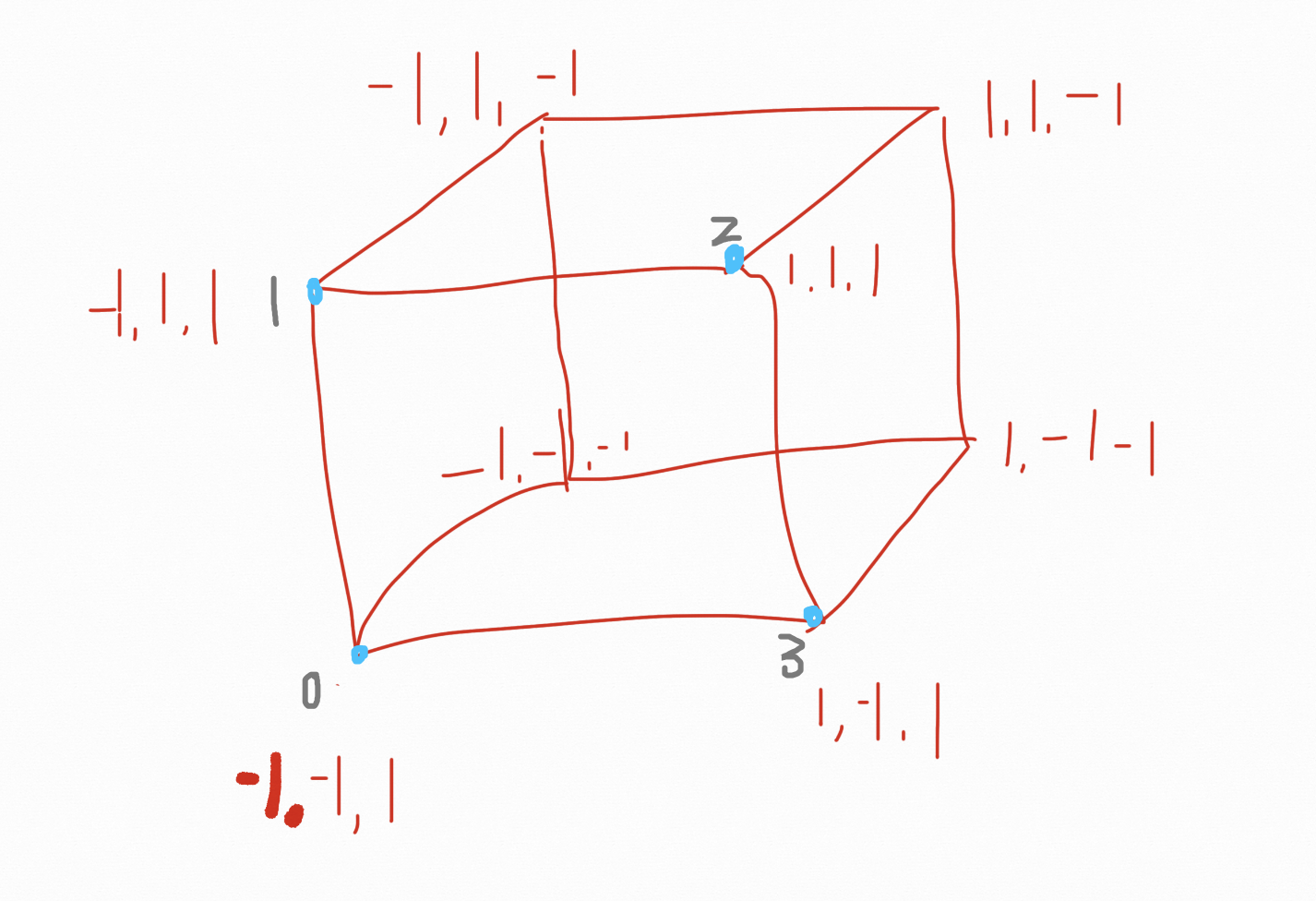
0-1-3 和 0-3-1绘制出来的三角面是有区别的，那就是顺时针和逆时针的区别，

所以，我们绘制面的时候，脑海中想象的要是外面儿并且按照逆时针绘制三角面，这样这个面才会如我们所想的那样展现出来。

所以绘制一个立方体要有如下步骤：

6个矩形面--->12个三角面--->36个顶点（三角面绘制的时候要按照逆时针顺序添加顶点）

 

最终效果: