Dijkstra算法的Java实现

package main.java;

import main.java.utils.GraphUtil;

import java.util.ArrayDeque;
import java.util.List;
import java.util.Queue;


/**
 * @Tme 2019/9/12 10:40
 * @Author chenhaisheng
 * @Email:ecjutsbs@foxmail.com
 */
public class DijkstraTest {

    //邻接矩阵的表示
    public final static double[][] GRAPH_DISTANCE = GraphUtil.getDijkstraGraph();

    //起点到某节点的临时最短距离
    public static double distance[] = new double[GRAPH_DISTANCE.length];

    //某节点的前驱节点
    public static int pre[] = new int[GRAPH_DISTANCE.length];

    static int originIndex = 0, toIndex = 4;


    public static void main(String[] args) {

        init();
        findDijkstraShortestPath();
    }

    /*
    **初始化distance[]   pre[]
     */
    public static void init() {

        for (int i = 0; i < distance.length; i++) {
            if (i == originIndex) {
                distance[i] = 0.0;
                continue;
            }
            distance[i] = Double.MAX_VALUE;
        }

        for (int i = 0; i < pre.length; i++) {
            pre[i] = -1;
        }
    }

    public static void findDijkstraShortestPath() {

        //queue用于保存尚待搜索的节点
        Queue<Integer> queue = new ArrayDeque<>();

        //起始，将起始节点添加到queue
        queue.add(originIndex);

        while (queue.size() != 0) {

            Integer currentIndex = queue.poll();

            //获取当前节点的out-edges
            List<Integer> neighbours = getNeighbours(currentIndex);

            for (int i = 0; i < neighbours.size(); i++) {

                //获取邻居节点的索引值
                int neighbourIndex = neighbours.get(i);

                //若起点经当前节点到邻居节点的距离 比直接到邻居节点的距离还小
                if (distance[currentIndex] + getDistance(currentIndex, neighbourIndex) < distance[neighbourIndex]) {

                    //更新起点到邻居节点的距离
                    distance[neighbourIndex] = distance[currentIndex] + getDistance(currentIndex, neighbourIndex);

                    //设置下一个节点的前驱节点为当前节点
                    pre[neighbourIndex] = currentIndex;

                    //由于distance[neighbourIndex]已经改变，因此需要重新搜索neighbourIndex
                    queue.add(neighbourIndex);
                }
            }
        }

        //输出从originIndex到toIndex的路径
        printPath(pre, originIndex, toIndex);
    }


    public static void printPath(int pre[], int from, int to) {

        //栈
        Deque<Integer> path = new ArrayDeque<>();

        path.push(to);

        int preIndex = pre[to];
        while (preIndex != from) {
            path.push(preIndex);
            preIndex = pre[preIndex];
        }

        path.push(from);

        while (!path.isEmpty()) {
            System.out.print(path.poll() + (path.size() > 0 ? "------>" : " "));
        }
        System.out.println(" ");
    }


    //获取当前节点所有的out-edges
    public static List getNeighbours(int index) {

        List<Integer> res = new ArrayList();

        //距离不为Double.MAX_VALUE,代表与当前节点连通
        for (int i = 0; i < GRAPH_DISTANCE[index].length; i++) {
            if (GRAPH_DISTANCE[index][i] != Double.MAX_VALUE)
                res.add(i);
        }
        return res;
    }

    public static double getDistance(int from, int to) {
        return GRAPH_DISTANCE[from][to];
    }
}

 

package main.java.utils;

/**
 * @Tme ${DATA} 19:10
 * @Author chenhaisheng
 * @Email:ecjutsbs@foxmail.com
 */
public class GraphUtil<T> {

    public static double[][] getDijkstraGraph(){
        double max=Double.MAX_VALUE;
        double[][] graph={
                {max,5,max,7,15},
                {max,max,5,max,max},
                {max,max,max,max,1},
                {max,max,2,max,max},
                {max,max,max,max,max}
        };
        return  graph;
    }
}

 

对应的图：

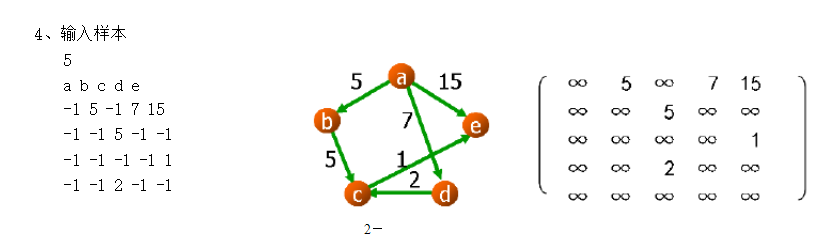
图的结构Ref：https://wenku.baidu.com/view/9fdeaa3c2b160b4e767fcff7.html

 

小结：

最重要的是记住：在搜索过程中，若节点i对应的distance[i]发生改变，那么对其任意一个邻居节点j，对应的distance[j]都要重新计算，继而引发连锁反应。

对某一个节点k，distance[k]通常会发生会多次改变。