【Leetcode940】不同的子序列 II

1.题目

给定一个字符串 s，计算 s 的 不同非空子序列 的个数。因为结果可能很大，所以返回答案需要对 10^9 + 7 取余 。

字符串的 子序列 是经由原字符串删除一些（也可能不删除）字符但不改变剩余字符相对位置的一个新字符串。

• 例如，"ace" 是 "abcde" 的一个子序列，但 "aec" 不是。

示例 1：

输入：s = "abc"
输出：7
解释：7 个不同的子序列分别是 "a", "b", "c", "ab", "ac", "bc", 以及 "abc"。

示例 2：

输入：s = "aba"
输出：6
解释：6 个不同的子序列分别是 "a", "b", "ab", "ba", "aa" 以及 "aba"。

示例 3：

输入：s = "aaa"
输出：3
解释：3 个不同的子序列分别是 "a", "aa" 以及 "aaa"。

提示：

• 1 <= s.length <= 2000
• s 仅由小写英文字母组成

2.分析思路

这个方法是一个acmer和我一起慢慢分析得出，大致过程就是动态规划。

设状态dp[i]: 以位置i结尾的子序列个数.如字符串“abc”

dp[0]=1,就一个a;dp[1]=2,以字符b结尾的子序列的数目：b、ab;dp[2]=4;c,ac,bc,abc;

abc的子序列个数为dp[0]+dp[1]+dp[2]=1+2+4=7;

---

如字符"aba"

dp[0]=1,a;dp[2]=2,b,ab;dp[3]=3,aa,ba,aba;

aba子序列的个数为dp[0]+dp[1]+dp[2]=1+2+3=6;

---

从上述分析可以得出，当字符串没有重复字符时，dp[i+1]=dp[i]+dp[i-1]+....+dp[0]+1;

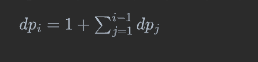
最后的子序列的个数：

---

但是当字符串中有重复子串的时候：

需要减去重复的值，并且更新i位置的dp[i]及之后的dp[i+1].....

如字符"aba"

dp[0]=1,a;

dp[2]=2,b,ab;

dp[3]=3=(4-1),aa,ba,aba,(a);

aba子序列的个数为dp[0]+dp[1]+dp[2]=1+2+3=6;

这我实现的不太好，使用了暴力方法进行遍历dp，更新dp，时间复杂度较高。

3.代码实现

class Solution {
    public int sum=0;
    public int summ(int a[],int num)
    {
        int results=0;
        for(int i=0;i<num;i++)
        {
            //System.out.println("遍历num:"+a[i]);
            results=(int)((results+a[i])%(Math.pow(10,9)+7));
        }
        return results;
    }
    public int distinctSubseqII(String s) {
        int results=0;
        Map<Character,ArrayList<Integer>>map=new HashMap<Character,ArrayList<Integer>>();//数据结构
        int leng=s.length();
        int nums[] =new int[leng];
        nums[0]=1;
        double M=Math.pow(10,9)+7;
        for(int i=0;i<s.length();i++)//获取是否重复的值
        {
            //ArrayList<Integer> list=new ArrayList<Integer>();
            Character c=s.charAt(i);
            boolean b = map.containsKey(c);
            if(b)
            {
                //System.out.println("存在"+b);
               ArrayList<Integer> value = map.get(c);
               value.add(i);
            }
            else
            {
                ArrayList<Integer> value=new ArrayList<Integer>();
                value.add(i);
                map.put(c,value);
            }
        }
        for(int i=1;i<s.length();i++)
        {
            sum=(int)((sum+nums[i-1])%(M));
            nums[i]=(int)((sum+1)%(M));
        }
        sum=(int)((sum+nums[s.length()-1])%(M));
        results=(int)sum;
        int dif[]={0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
        if(map.size() !=s.length() && map.size()!=1)
        {
            for(int x=0;x<s.length();x++)
            {
                int t=s.charAt(x)-'a';
                if(dif[t]!=0)
                {
                    nums[x]=(int)((nums[x]-dif[t])%(M));
                    if(nums[x]<0)
                    {
                         nums[x]+=(int)M;
                    }
                    int index=x;
                    sum=(int)((summ(nums,index+1))%(M));
                    while(index<(s.length()-1))//求新的dp
                    {
                        //Character key=s.charAt(index);
                        nums[index+1]=(int)((sum+1)%(M));
                        sum=(int)((sum+nums[index+1])%(M));
                        index++;
                    }
                }
                dif[t]=(int)((dif[t]+nums[x])%(M));
            }
            results=summ(nums,s.length());
        }
        else if(map.size() == 1)
            results=s.length();
        return results;
    }
}