五二不休息,今天也学习,从JS执行栈角度图解递归以及二叉树的前、中、后遍历的底层差异

壹 ❀ 引
想必凡是接触过二叉树算法的同学,在刚上手那会,一定都经历过题目无从下手,甚至连题解都看不懂的痛苦。由于leetcode不方便调试,题目做错了也不知道错在哪里,最后无奈的cv答案后心里还不断安慰自己。不甘心想着要不直接背模板吧,可当天一知半解的记住了,不到半个月回头面对一道曾做过的简单二叉树题,脑袋里跟看一道新题一样。
那么二叉树对于我这个不是计算机专业的人来说难在哪呢?第一,我始终无法在脑中构建递归的过程,就像我的思维空间不足以支撑递归在我的脑中运行,大致脑补了两步就直接乱套了,我想象不出这个过程。
第二,对于二叉树的前中后层序遍历始终是一知半解,因为不理解递归到底怎么运行的,所以心里其实不知道它们三者到底差异在哪,为啥arr.push(root.val)写的地方不同,就实现了三种不同遍历方式?小小的脑袋里留下了大大的疑惑。
const traverse = (root) => {
if (root === null) {
return;
};
// 前序遍历
traverse(root.left);
// 中序遍历
traverse(root.right);
// 后序遍历
}
那么本文就是为了解答这些疑问而来,我将从递归说起,用图解JS调用栈的方式阐述递归思路,帮助大家在脑中构建这个过程,之后再解释二叉树前中后序遍历为什么逻辑处理的位置不同,就能达到不同差异,那么本文开始。
贰 ❀ 从递归说起
我先来聊聊如何理解递归,倘若问你什么是递归?我想大部分人脑袋里马上冒出函数自己调用自己就是递归,确实没错。概念虽然简单,可是随手写一个简单的递归又得思索很久,那么我们先来总结递归的几个需要注意的点:
- 函数得自己调用自己
- 你只用关注函数第一次调用应该做什么,不需要关注之后递归做什么,因为递归会帮你做第一次相同的操作
- 你需要考虑什么条件下终止递归
- 每次递归是否需要设置返回值?不返回能不能解决当前问题
那么现在问题来了,给一个数组[1, 2, 3],要求正序输出数组中的每个元素?很简单,一个while循环搞定:
const arr = [1, 2, 3];
// 正序遍历
let i = 0
// 跳出条件
while (i < arr.length) {
// 当前要做什么?
console.log(arr[i]); // 3 2 1
i++;
};
现在要求用递归的方式做相同的操作,我们先将递归的几个要点套到这个for循环中,分析下递归时应该做什么:
- 自己调用自己不用说了,硬性条件
- 每一步只是做
console.log(arr[i])以及让i自增 - 正序遍历,当
i = arr.length时就得跳出递归 - 没有返回值,不需要考虑
思路非常清晰了,现在来用递归来实现这个过程:
const traverse = (arr, i = 0) => {
// 跳出条件
if (i >= arr.length) return;
// 第一次调用做什么?输出arr[i];
console.log(arr[i]); // 1 2 3
// 自己调用自己
traverse(arr, i + 1);
};
traverse(arr);
我在 一篇文章看懂JS执行上下文中提到,函数每次调用都会创建一个全新的函数上下文,且它们满足先进后出的特点被存放在JS执行栈中,因为上述递归的过程如下:
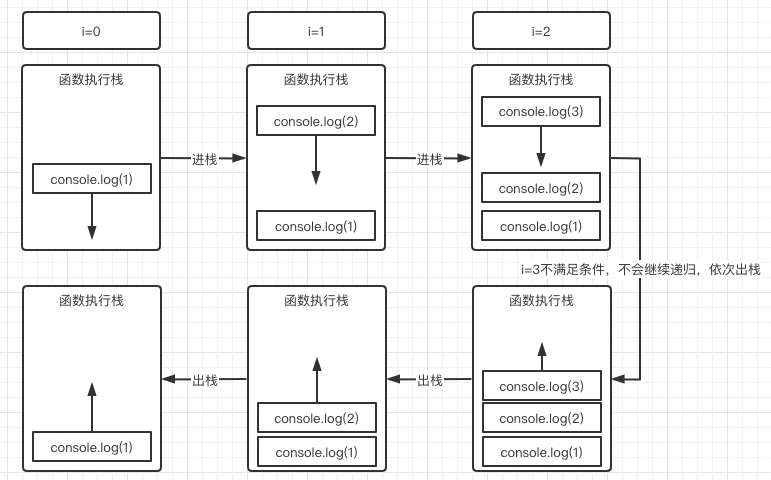
可以看到一开始执行栈为空,然后递归开始,依次创建三个函数进去,直到i === arr.length不满足条件跳出递归,这时候不会继续创建新的函数调用;
而之前的函数体内只做了console.log(arr[i])一件事,由于不需要继续创建新的调用,既然执行后完毕了所以开始依次出栈,直到整个调用栈为空,到此整个递归结束。
所以为什么这个递归能达到正序输出的效果呢?其实是因为输出动作在前,创建新的递归在后,我输出1的时候,输出2的递归都还没创建呢,当然能正序输出了。(记住这句话,后面要考)
还是这个数组,现在我们要求倒序输出它,请你以遍历和递归两种方式分别实现,怎么做?我想经过前面的讲解,大家不假思索就能写出如下代码:
// 倒序遍历
let i = arr.length - 1;
// i>=0我还能继续做一件事
while (i >= 0) {
console.log(arr[i]); // 3 2 1
i--;
};
不知道大家有没有发现,只要我们用while去遍历一个数组,这个while的操作甚至已经告诉了我们这个倒序递归应该怎么写:
const traverse = (arr, i = arr.length - 1) => {
// i<0我不能继续做一件事
if (i < 0) return;
// 第一次调用做什么?输出arr[i];
console.log(arr[i]); // 1 2 3 4 5 6
// 自己调用自己
traverse(arr, i - 1);
};
traverse(arr);
因为递归是什么情况下我们不能做一件事,而while是什么情况下我们能做一件事,因此递归的条件总是跟while相反。
那么到这里,我们总结了一个很有趣的概念,当你不会写递归时,就想想我用while怎么遍历实现,while写好了,定义一个tarverse函数,然后跳出递归的条件与while相反,再将while要做的事情照搬过来,最后加一个函数自调用,递归也就完成了,是不是很简单,这个思路也是模板的一种。
叁 ❀ 执行栈的先进后出
你以为到这就要结束了?当然不,现在问题再升级,同样还是上面的数组,同样还是倒序遍历,但是此时我们要求递归的写法不能跟while一样让i递减,请让i递增的同时倒序输出数组,怎么做?
还记得上文我是怎么解释正序递归是为什么能正序输出数组的吗?因为做一件事的动作在递归调用之前,这样就保证了1永远在2后面先输出,那怎么倒序的?很简单,把你要做的事放在递归调用之后即可:
const traverse = (arr, i = 0) => {
if (i >= arr.length) return;
traverse(arr, i + 1);
console.log(arr[i]); // 3 2 1
};
traverse(arr);
为什么放到后面就能达到倒序遍历?因为JS的执行栈是先进后出的,我们来解释下这个过程:
i=0时,满足条件,结果遇到了traverse(arr, i + 1),这时候创建一个新的函数上下文,且这个函数不执行完毕,后面的console.log根本无法执行,所以等着。i=1时,同上,又遇到了traverse(arr, i + 1),继续创建新的函数上下文,第二个函数的console.log也等着了。i=2时,同上,又遇到traverse(arr, i + 1),继续创建新的上下文。i=3时,不满足条件直接返回,执行完毕,此时是不是表示i=2的traverse执行完成了,那么i=2的console.log不就可以执行了,于是第一输出了3。i=2创建的上下文执行完毕,标注i=1的traverse执行完了,它也能执行后面的console.log了- 于是输出了
3 2 1。
我们要做的事其实是console.log,但是因为traverse(arr, i + 1)在前,遇到就得不断的创建,导致console迟迟不能触发直到递归跳出。而js执行栈是先进后出,那么最后进栈的肯定console.log先执行,本质上就是借用了先进后出的后出,来模拟了倒序的过程。
怕大家容易忘记,那到这里我们先总结下当下学到的知识点:
- 不会写递归?那就写好
while,将while的条件改成相反就是递归的跳出条件,因为while是满足什么条件做一件事,递归是不满足某个条件不做一件事,之后将while做的事照搬给递归即可,这里不需要考虑这件事应该放在递归前还是后。 i同等自增或自减情况下,可以将做一件事的行为放在递归调用的前或者后,便能达到正序或倒序遍历的效果。- 正序和倒序的底层差异其实就是执行栈的先进后出,正序是先进(先把事做了再进),倒序是后出(啥也别做先进,出的时候再做一件事)
肆 ❀ 用执行栈看二叉树前、中、后序遍历差异
在上文,我们用一个最基本的数组正序,倒序遍历的例子,解释了i自增情况下,为什么console放在递归前后位置不同,能达到正序和倒序的效果,其本质原因就是借用了执行栈的先进后出,先做一件事再递归,还是先不断递归,出栈的时候再做一件事的区别。
而现在我们再回头看看文章开头二叉树的模板,现在我们来解释下为什么一件事丢在三个不同的位置,能达到三种遍历效果,我们假定有一颗最基本的二叉树:
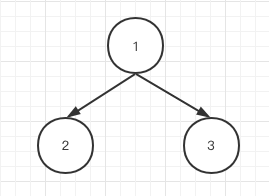
很明显,前序遍历应该输出1,2,3,后续遍历应该输出2,3,1,中序遍历应该输出2,1,3。我们先解释前序和后续。
前序的的模板可以定义为:
const traverse = (root) => {
if (root === null) {
return;
};
console.log(root.val);
traverse(root.left);
traverse(root.right);
}
由于每个节点都可能会有自己的左右子节点,所以现在这段代码是不是就非常好理解,我不管你有没有子节点,到了某个节点咱先输出,之后再考虑递归的事,而traverse(root.left)又在traverse(root.right)之前,所以某个节点的左子节点一定会在右子节点之前输出。
有同学可能就要想了,如果这颗二叉树非常复杂呢?我们在文章开头递归处已经说了,你只用考虑当前函数调用应该做什么,后面递归会帮你做相同的事情,即便这颗二叉树是下图这样:
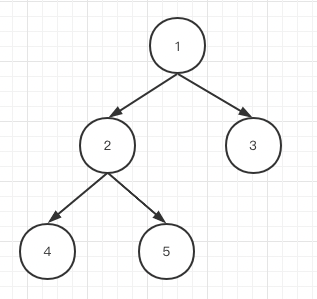
到了节点2,它一样会让4,5在3前面输出,毕竟2,4,5都可以理解成1的左子树,整体优先级比3高,其实就是这么个道理。
那么后序遍历是怎么回事呢?后序的代码其实是这样:
const traverse = (root) => {
if (root === null) {
return;
};
traverse(root.left);
traverse(root.right);
console.log(root.val);
}
前文已经知道,因为traverse递归行为在前,这就导致所有节点没被递归完之前,console一个都会输出,而因为执行栈先进后出的特色,这就导致子节点的输出一定比父节点要早(参照前文数组的倒序遍历),而traverse(root.left)又在traverse(root.right)之前,那么顺序是不是就是(子left节点 > 子right节点) > 父节点,你看不就是这么一回事,不难理解吧?
有同学可能就马上想到了,不对吧,按照执行栈先进后出,traverse(roo.left)不是在traverse(root.right)前面先入栈,根据先进后出的规则,后进的应该先输出才对,那为什么不是3, 2, 1的输出,而是2, 3, 1?
首先,子节点肯定早于父节点输出,我想着点大家肯定没疑问,接下来我们还是画图,解释这个过程:
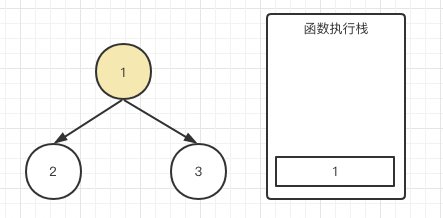
首先根节点1,因为它有左右子节点,console肯定没办法输出,我们理解为先进栈存起来。紧接着调用traverse(root.left)
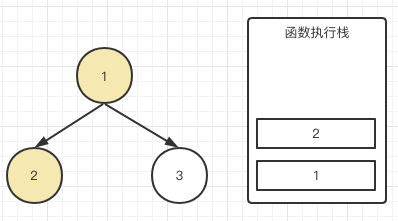
我们也不知道2有没有子节点,反正也不能立刻输出,也把2存起来。
注意,那么此时traverse(root.right)该运行了吗?我们知道js的同步执行是,某一步逻辑没跑完,后面的逻辑就得等着前面的逻辑走完,那是不是只要traverse(root.left)没递归完,就轮不到traverse(root.right)运行?
因此,我们继续判断让2的左子节点递归,但是很遗憾traverse(2.left)是null,是不是直接return;既然不用继续递归了,那就标明可以运行traverse(2.right)了,结果又是是null导致return,那是不是又能走下一步了,console.log(2),于是2第一个被输出了。
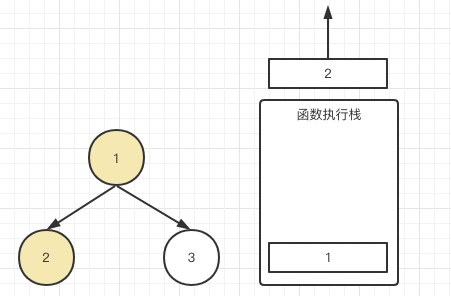
于是在3还没递归前,节点2已经出栈了都,由于2(可以理解为1.left)执行完成,那表示终于可以执行1.right也就是节点3了,于是3进栈:
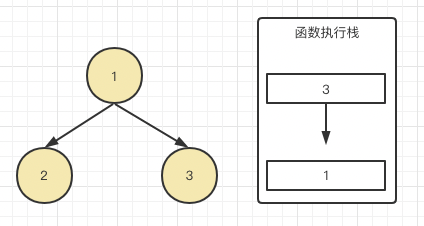
节点3也没有左右子节点,顺利也输出了3,节点3递归结束,也出栈,终于根节点的两个节点都递归完成,是不是根节点的console也能执行了?所以顺序就是2,3,1了。
那么到这里,我们通过调用栈的形式解释了二叉树的前序、后续遍历。
那么中序遍历是怎么回事呢?通过前文的解释,大家可以脑补下中序的过程,其实本质差异在于,根节点要做的事情,得左子树全部递归完成,然后左子树做完了,问根节点,嘿兄弟,你可以做我做的不要事了,然后根节点输出后,卑微的右子节点接着做。
所谓二叉树的前中后序遍历,不就是这么回事么。那么到这里,我们总结下三种遍历的区别:
前序遍历:每个节点都可以理解成一个根节点,在递归当前节点左右节点前,咱们先把要做的事情做了。(前序遍历总是能拿到当前节点信息)
中序遍历:左子树递归完成,把要做的事情做了,然后根节点才能做相同的事,最后这件事才轮得到右子树做。
后续遍历:根节点要做的事往后排一排,左子树做完右子树做,最后轮到根节点做。(后续遍历总是能将子节点信息返回给自己的父节点)
凡是二叉树遍历,大家不要一开始就在脑中构建一个非常复杂的树,跟我一样,就1, 2, 3三个节点,然后回顾我上面提到的过程,通过这种方式,是不是二叉树遍历模板也非常透彻的理解了呢?
伍 ❀ 总
本来想接着讲讲二叉树层序遍历,出于篇幅问题层序遍历还是留着下篇文章继续说,那么通过本文,我们知道了如何通过递归遍历一个数组,以及如何将while改写成一个递归。
之后我们通过执行栈解释了为什么将要做的步骤放在递归前后能达到正序/倒序遍历数组结果,从而引出了二叉树前序、中序、后序遍历的本质差异,那么到这里,我相信你对于递归,以及二叉树的基本遍历又有了更深入的理解。
五三想休息,明天也学习,那么下篇文章见。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号