JS Leetcode 213. 打家劫舍 II 题解分析，在动态规划基础上感受分治算法的魅力
壹 ❀ 引
本题来自LeetCode 213. 打家劫舍 II，难度中等，属于前面我们做过的198. 打家劫舍的升级版，难度同样为中等，题目描述如下：
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。
示例 1：
输入：nums = [2,3,2] 输出：3 解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。示例 2：
输入：nums = [1,2,3,1] 输出：4 解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。 偷窃到的最高金额 = 1 + 3 = 4 。示例 3：
输入：nums = [0] 输出：0提示：
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 1000
这里我还是推荐先尝试简单点的版本，因为核心思想不变，想做此题，还是得掌握动态规划解法的核心思想，上一道题的题解为JS Leetcode 198. 打家劫舍 题解分析，那么我们开始分析本题。
贰 ❀ 分治算法+动态规划
在上道题中，我们已经介绍了此题动态规划的核心思想，并推导出动态规划转移方程，即：
dp[i] = Math.max(dp[i-1], dp[i - 2] + nums[i]);
翻译过来就是第i家最大收益dp[i]，为当前偷的这一家的收益 + 上上家收益与上家收益的最大值，比如例子1,4,2。到第三家时，我们能拿到的最大收益为Math.max(4,1+2)，所以最终得到4。
而今天这一道题的唯一差异在于，现在的房屋形成了一个环。还是以[1,4,2]为例，两者的区别：
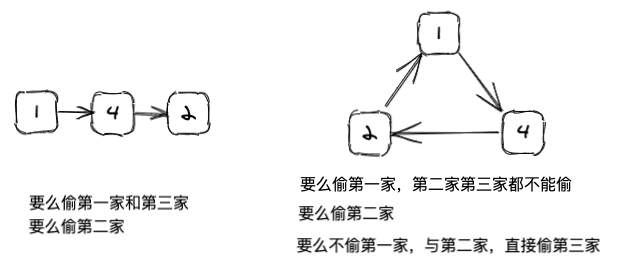
因为环的缘故，1，3家可以理解成并排的两家，所以没办法一起再偷了，才导致了右边这三种情况。有同学可能就想了，那为什么左边这种不存在只偷1，或者只偷第三家的情况呢？原因是上道题的房屋并不是环，且1，3一起偷并不冲突，能偷白不偷，总不可能存在偷了1，3两家的和比其中一家还小的情况吧。
让我们从简单的例子开始推倒，比如[1,4,2]，按照上面的方案，可分为：
- 不偷第一家，偷第二家或者第三家，看这两家中间谁更大，很明显4更大。
- 不偷最后一家，偷第一家或者第二家，看这两家中谁更大，很明显4更大。
- 第一家和第三家都不偷，直接偷第二家，很明显只能是4。
但是如果我们仔细思考，所谓第三种偷法，即不偷第一家和第三家只偷第二家的这种可能性，其实已经被包含在前两种偷法中了，因为如果中间这家最大，它总是能被找出来，比如第一种偷法因为4>2，导致最后还是只偷了第二家，而如果中间这家很小，它也总是能被排除掉。
我们最终得到了两种偷法，即要么不偷第一家，要么不偷最后一家，那知道了这个我们又该如何求出最大收益呢？到这里，我们需要引入一个很重要的概念，分治算法。
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。---百度百科
所谓分治，即是分而治之（将一个问题的不同情况拆开分别处理），将一个大问题，拆分成多个小的且与原问题性质相同的问题。比如上面因为环的缘故，我们要么不偷第一家，从后面的收益中找最大收益，要么不偷最后一家，从前面的收益中找到最优解。那是不是可以直接分两种情况，分别求出小问题的最优解，然后总结这两者，找出全局问题真正的最优解呢。
综合上述，我们可以假定不偷第一家的最佳收益为P1，不偷最后一家的最佳收益为P2，那么全局最佳收益即是Math.max(P1,P2)，而P1，P2的问题已经降级为昨天那道题的思路了，所以让我们来实现这段代码：
/**
* @param {number[]} nums
* @return {number}
*/
var rob = function (nums) {
if (nums.length === 0) {
return 0;
};
if (nums.length === 1) {
return nums[0];
};
if (nums.length === 2) {
return Math.max(nums[0], nums[1]);
};
// 照搬上道题的方法
let findMax = function (nums) {
let n = nums.length;
let dp = new Array(n + 1);
dp[0] = 0;
dp[1] = nums[0];
for (let i = 2; i <= n; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
};
return dp[n];
};
// 不偷第一家，所以i从1开始
let P1 = findMax(nums.slice(1));
// 不偷最后一家，所以结尾为length-1
let P2 = findMax(nums.slice(0, nums.length - 1));
return Math.max(P1, P2);
};
代码看上去很长，其实大部分代码都是照搬了上道题的思路，那么本题就分析到这里了。
