JS Leetcode 264. 丑数 II 题解分析,当暴力无法暴力,让我们弃武从文了解三指针
壹 ❀ 引
我在JS Leetcode 263. 丑数 题解分析,来认识有趣的丑数吧一文中记录了简单难度的丑数题,那么这篇题解是它的升级版,题目来自LeetCode264. 丑数 II,题目描述如下:
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。
示例 1:
输入:n = 10 输出:12 解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。示例 2:
输入:n = 1 输出:1 解释:1 通常被视为丑数。提示:
- 1 <= n <= 1690
让我们开始解析这道题。
贰 ❀ 题意分析
其实我在最初看到这道题的时候,我表示题目都没看懂....那么我们先理解下这道题说了什么,我们已经知道,所谓丑数就是能被质因数2,3,5整除的数,那么这道题就是让你自己去产生丑数,比如第一个例子10。
因为提示说明1<=n<=1690,所以我们让n从1自增,一直遍历到10,看看能产生哪些丑数。
当n是1时,1分别乘以2,3,5,得到[1,2,3,5],为什么有个1?因为题意说了1通常也被视为丑数。
当n是2时,2又分别乘以上次得到的数组[1,2,3,5],于是我们得到了[1,2,3,5,4,6,10],为方便理解,我们不记录重复的数字。
当n是3时,3又分别乘以[1,2,3,5,4,6,10],于是我们得到了[1,2,3,5,4,6,10,9,15,12,18]。
继续操作.......
当n是10时,于是我们得到了一个庞大的,且数字都是丑数的数组,我们将其排序,得到[1,2,3,4,5,6,8,9,10,12,15,20...],让我们找到第10个数字,最终得到12,所以12是我们想要的答案。
PS:我最初的想法,是n每次自增都分别乘以2,3,5,但其实这个思路有个很麻烦的问题,比如当i为7时,7*2=14,而14并不是一个丑数,所以保险做法是永远用丑数去生成新的丑数,而且也不会漏掉任何一个丑数。
这是我最初的错误思路,很明显当 i 为7,就记录了14,21,35这种非丑数的数字:
/**
* @param {number} n
* @return {number}
*/
var nthUglyNumber = function (n) {
let arr = [1];
let i = 1;
while(i<=n){
// 分别乘以质因数并加入数组
arr.push(i*2,i*3,i*5);
i++;
}
// 去重,以免重复数字浪费位置
arr = [...new Set(arr)].sort((a,b)=>a-b);
return arr[n-1];
};
叁 ❀ 想暴力却暴力失败的做法
通过上面丑数生成丑数的分析,我们直观的暴力做法就是先声明一个包含1的数组,然后让n从1开始自增遍历,并分别乘以2,3,5得到新的丑数保存到数组,之后让n自增,再继续乘以数组中所有丑数得到新的一批的丑数并填充到数组(可以考虑去重),一直遍历到n结束,排序并返回第n个数字即可。
让我们来实现这个逻辑:
var nthUglyNumber = function (n) {
let arr = [1];
let i = 1;
while (i <= n) {
// 分别乘以质因数并加入数组
for (let j = 0; j < arr.length; j++) {
arr.push(j * 2, j * 3, j * 5);
};
// 去重,相同的数字就不要参与后续的计算了
arr = [...new Set(arr)];
i++;
}
// 那么到这里一定能得到一个长度是10的数组,让我们排序它
arr = arr.sort((a, b) => a - b);
return arr[n - 1];
};
看似很完美,其实仔细想想,如果n足够大,我们会得到一个足够长的数组参与下次计算,而这个过程直接导致了爆栈....
FATAL ERROR: CALL_AND_RETRY_LAST Allocation failed - JavaScript heap out of memory
那么到这我们不禁就想,能不能每次都按照新的丑数,生成已经排序好的丑数呢?因为如果我们可以直接生成一个有序的丑数数组,当数组长度达到n,说明就没必要继续遍历下去了,能大大的节省遍历时间。所以接下来我们来介绍三指针做法。
叁 ❀ 比较绕的三指针做法
这个过程可能有点绕,我们来举例说明,为了方便理解,我们就假设n=4,那么当 n 为1时(此时数组中只有一个1,前面也说过,此时的思路我们以丑数生成丑数,而不是以n生成丑数),我们用已知丑数1乘以三个质因数,所以会得到三个新丑数[2,3,5]:
图1
既然想让数组直接有序,那么此时我们应该加到数组的就应该是三个数中最小的,也就是2,于是把2记录到数组中。
那么问题来了,剩下的3,5我们其实还是需要继续使用的,因为当n为2,我们使用[1,2]再次生成新丑数,我们会得到[4,6,10],很明显3比[4,6,10]都要小,因此第一次取最小数之后,[3,5]仍然需要参与后续的比较,因为它们都可能是接下来比较中的最小数。
第二个问题,第一次生成新丑数时,丑数数组[1]的1已经参与过计算了,而当第二次生成丑数的时候此时数组为[1,2],难道丑数1还要再次参与计算,然后又得到一个2再次参与比大小?怎么绕过呢?
让我们设想一下,此时有三个指针分别为2,3,5服务,它们为i2,i3,i5且一开始指针都指向0,nums[0]也就是丑数1。
在第一次计算后我们得到了2,3,5并取了最小数字2,前面说了,3,5其实是需要参与后续的比较的,所以为3,5服务的指针保持不动,下次计算的时候,由于i3,i5还是指向数组中的第一个数字nums[0]也就是1,所以还是能得到nums[i3]*3 = 3,nums[i5]*5 = 5两个结果,这样我们就解决了3,5不会跳过的问题。
而为丑数2服务的指针i2已经产生了新的丑数,它就没必要继续指向0了,而是自增往右移动一位。为什么要右移?还记得我们前面的规则吗?永远是用丑数产生新的丑数,你也许会想,移动了不会漏掉丑数吗?别忘了,i3和i5此时的指针都还是0,它们还是会产生3和5,只有产生最小的丑数并加入了数组,指针才会右移,就这样有序的进行,怎么会漏数字呢?
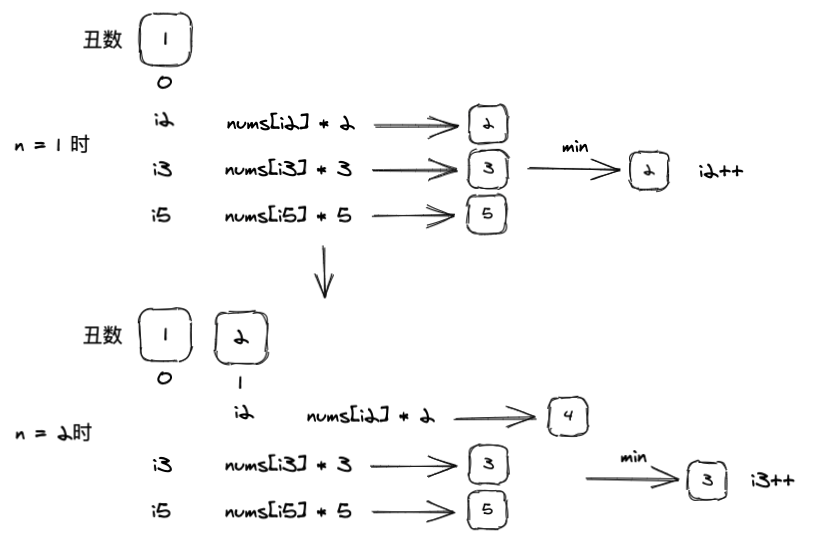
让我们来实现这段代码:
/**
* @param {number} n
* @return {number}
*/
var nthUglyNumber = function (n) {
let i2 = 0;
let i3 = 0;
let i5 = 0;
// 声明一个长度是n的数组,记得默认有个丑数1
let res = new Array(n);
res[0] = 1;
for (let i = 1; i < n; i++) {
let min = Math.min(res[i2] * 2, res[i3] * 3, res[i5] * 5);
// 记录最小值加入到数组
res[i] = min;
// 记得,只有产生了最小丑数的指针,需要右移
if (min === res[i2] * 2) { i2++ };
if (min === res[i3] * 3) { i3++ };
if (min === res[i5] * 5) { i5++ };
};
return res[n - 1];
};
如果觉得还有点绕,可以尝试断点,结合上面的图画一画,那么本文就到这里了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号