JS Leetcode 81. 搜索旋转排序数组 II 题解，补救二分法的可行性

壹 ❀ 引

今日LeetCode题为153. 寻找旋转排序数组中的最小值，在10个月前，我已在JS leetcode 寻找旋转排序数组中的最小值 题解分析，你不得不了解的二分法一文中写了本题的题解，所以今日的题就不用再写博客记录了。而昨天的题81. 搜索旋转排序数组 II因为思路问题，我先记录了它的普通版33. 搜索旋转排序数组，所以按照约定，今天得把这道题的题解补回来，题目描述如下：

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

提示：

1 <= nums.length <= 5000
-104 <= nums[i] <= 104
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104

进阶：

这是 搜索旋转排序数组 的延伸题目，本题中的 nums 可能包含重复元素。
这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

我们先来搜集题目信息，再开始实现它。（这篇文章本来应该昨天发，中午写了一半，晚上加班发版到凌晨1点半，苦不堪言....）

贰 ❀ 题解分析与二分法

我还是推荐，在做本题前，先阅读33. 搜索旋转排序数组一文，因为本题的解题思路将与昨天那篇文章高度相同，仔细阅读题目，会发现唯一不同的地方在于数字不必互不相同，即数组存在重复项，我们以[0,1,1,1,1]寻找0为例，它的旋转情况如下图：

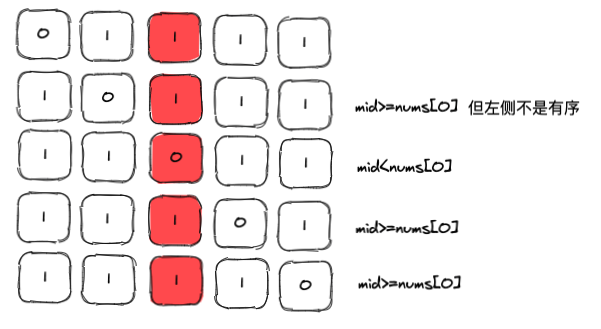
还记得我们上一题的二分规则吗，根据mid与nums[0]的大小对比，判断有序部分在mid的左侧还是右侧，找到了有序部分，就能利用target>=start&&target<mid（有序在左侧）或者target>mid&&target<=end（有序在右侧）来决定放弃掉另一半元素。

但根据上图的第二行，假设旋转为[1,0,1,1,1]，虽然mid>=nums[0](为什么是>=上篇文章也有解释)，但mid左侧部分居然不是一个有序序列，这就会导致我们的思路不可行，因为重复数字的出现，打破了我们原有二分法的规则，如果挽救这种二分特性呢？其实要做的很简单，如果此次查询出现了左右相等的情况，我们将任意一侧的指针，比如r--，然后不进行后续逻辑跳出循环，相当于重置程序，直到两侧不会出现相同数字，或者重置过程中因为也会重新计算mid遇到target，比如下面这个例子：

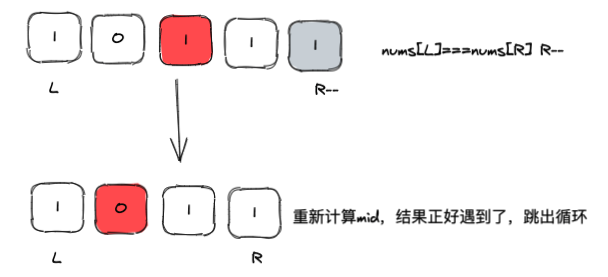
当然这个例子显得有些巧，但即便是没遇到，我们也会将数组转变成[1,0]后再进行前面根据mid与nums[0]以及target的比较。

你也许会想，去除掉相同数字不会影响最终结果吗？但我们只是想在数组中找到目标元素，相同的元素本来存在一个就够了，如果数组不存在相同元素，那这题不就是昨天做的那道题了...而本题只是增加了重复元素故意作为了新的考点。

可能看到这，大家还是无法理解为什么为什么这种操作就挽救了前面提到的二分特性，其实问题的根本，只是因为重复元素的存在，导致可能出现左右两侧都是相同元素的情况，比如前面的[1,0,1,1,1]，就让我们前面二分法公式无法套用。

大家可以多列几个例子自行验证，所以这道题的解法，仅仅是在昨天那道题的代码基础上，做了一个当左右指针元素相等时修改指针的操作而已，代码如下：

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {boolean}
 */
var search = function (nums, target) {
    let l = 0;
    let r = nums.length - 1;
    while (l <= r) {
        const mid = Math.floor((l + r) / 2);
        // 如果mid就是目标值直接返回
        if (nums[mid] === target) {
            return true;
        };
        // 开始处理左右相同数字的情况
        if (nums[l] === nums[r]) {
            r--;
            // 继续判断还有没有相等的情况，直接跳过后续逻辑
            continue;
        };
        // 下面的逻辑与上一道题一模一样
        if (nums[mid] >= nums[l]) {
            //target 在 [l, mid] 之间
            if (target >= nums[l] && target < nums[mid]) {
                r = mid - 1;
            } else {
                //target 不在 [l, mid] 之间
                l = mid + 1;
            };
        } else {
            // [mid, r]有序
            // target 在 [mid, r] 之间
            if (target > nums[mid] && target <= nums[r]) {
                l = mid + 1;
            } else {
                // target 不在 [mid, r] 之间
                r = mid - 1;
            }
        }
    }
    return false;
};

所以这道题，只是增加了下面这一小段代码（你让l++也行）：

if (nums[l] === nums[r]) {
    r--;// 或者l++都行，目的就是为了修复二分行，不让上面那种极端情况出现
    continue;
};

而这一小段代码，就像是在不满足二分法情况下，再给程序一次机会一样，不会再修复二分特性，让程序能继续按照我们上道题的思路进行二分，从而判断出最终结果。