JS Leetcode 74. 搜索二维矩阵题解分析，二分法与坐标轴法

壹 ❀ 引

本题来自Leetcode74. 搜索二维矩阵，虽然难度是中等，但如果站在做出来的角度，你会发现其实并不难，题目描述如下：

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true
示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

贰 ❀ 简单的题解分析

我们简单提取下题目信息，给定一个二维数组，每个子数组都满足升序排列，且每后一排子数组的第一个元素，一定大于上一排子数组的最后一个元素。而题目要求就是给定一个目标值，让我们在这个二维数组中查询，如果存在返回true，不存在则返回false。

贰 ❀ 壹 暴力解法

我们可以直接遍历数组中的每个子数组，相当于完整遍历一次所有数字，从头到尾看是否有与目标值相同的值即可，思路清晰且简单，这里就不贴实现代码了。

贰 ❀ 贰 二分法

我在JS leetcode 寻找旋转排序数组中的最小值 题解分析，你不得不了解的二分法一题中，曾简单科普过二分法，相对于暴力做法时间复杂度O(n)，二分法因为每次查找都只需要考虑一般的元素，所以时间复杂度为O(logn)，所以我当时看到此题，第一想法是给数组降维，然后直接套用二分法的模板，直接上代码：

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
    // 打平为一维数组
    let arr = matrix.flat(2);
    // 使用二分法进行查找
  	// 定义左边界
    let l = 0;
  	// 定义右边界
    let r = arr.length - 1;
    while (l <= r) {
      	// 取中间数
        mid = Math.floor((l + r) / 2);
      	// 如果相等直接返回
        if (arr[mid] === target) {
            return true;
        } else if (arr[mid] < target) {
            l = mid + 1;
        } else if (arr[mid] > target) {
            r = mid - 1;
        };
    };
    return false;
};

因为数组的子数组都满足升序，且后面的元素必定大于前面的数组，即便我们降维后依旧满足整体数组为升序数组的条件，因此可以使用二分法。

我们每次都找中间数，判断是否与目标数相等，相等直接返回。但如果不相等，就需要区分与目标数的大小差异了，如果中间数比目标值要小，那说明目标数必不可能在中间数的左边区间，因此需要修改左边界后，开始继续查找右边区间，反之亦然。

贰 ❀ 叁 坐标轴法

我在逛题解时，看到了一个让我眼前一亮的做法，那就坐标轴法，题解灵感来自于【坐标轴法】搜索二维矩阵

这个思路其实非常好理解，我们来看个坐标图，以题目中二维数组为例：

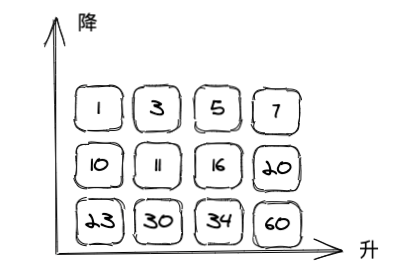
每行数组都满足升序，第一个最小，越往右边越大。

每列数组从下往上满足降序，越往上越小，且每行数组最后一个数都比下一列第一个数小。

我们用图将例子中查找3的过程画出来就是这样：

思路很简单，倒序查找二维数组，因为最后一行第一个数都比3大，而且我们已知每行数组是升序，那说明这一行后面的数字都不用看了，直接看上一行。

第二次从倒数第二行开始查找，结果10还是比3大，这一行后面的数组也不用看了，继续往上。

第三次我们遇到了1，这次1比3要小，因为每行数组是升序，我们继续看看1后面的数字有没有跟3相等的，结果很幸运，我们找到了目标值，返回true即可。

我们用代码表示这个过程：

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
    // 分别定义x轴与y轴计数
    let y = matrix.length - 1, x = 0;
    while (y >= 0 && x < matrix[0].length) {
        if (matrix[y][x] === target) {
            return true;
            // 如果某排数组第一个元素都比目标值大，y轴上移
        } else if (matrix[y][x] > target) {
            y--;
        } else {
            // 反之x轴右移
            x++;
        }
    };
    return false;
};

注释和图解都很详细了，那么本题就记录到这里了。