JS Leetcode 304. 二维区域和检索 - 矩阵不可变,彻底弄懂二维数组前缀和

壹 ❀ 引
我在JS LeetCode 303. 区域和检索 - 数组不可变,一维数组的前缀和一文中,记录了一维数组求区间合的解题思路,正好还有一题的升级版,题目来自leetcode304. 二维区域和检索 - 矩阵不可变,实不相瞒,我在看题解理解的过程中就花了不少时间,所以这里会写的格外详细一点,题目描述如下:
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。
示例:
给定 matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5] ] sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12提示:
你可以假设矩阵不可变。
会多次调用 sumRegion 方法。
你可以假设 row1 ≤ row2 且 col1 ≤ col2 。
贰 ❀ 暴力解法
其实我在看此题的时候一开始就不理解为什么(row1, col1) = (2, 1)对应矩阵中的2,按照我们我们电影院找座位的习惯,应该是第二排的第一个才对,难道不是5?后来想到这里的矩阵其实是二维数组,数组索引起点是0,这才想明白对应的其实是第三排的第二个,因此左上角是2,右下角同理。
在前面一维数组前缀和的题解中,我们已经知道了如下公式(若不理解请先阅读一维数组前缀和题解):
sumRange(i, j) = preSum[j + 1] - preSum[i]
那么站在本题的角度,我们是不是也可以分别求每行数组的前缀和,再根据区间差得到二维数组的区间和呢?我们从一个简单的二维数组开始理解,如下有二维数组[[1,1,1],[1,1,1],[1,1,1]],我们需要求(1,1,2,2)的区域和:
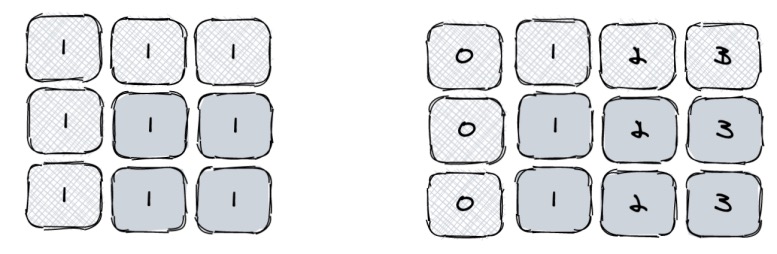
看图就知道答案是4,所以对应到右边的一维数组前缀和中,因为有两行数组,套公式应该是:
// 有两行,因此是两个sumRange相加
sumRange(1, 2) + sumRange(1, 2)
// 等同于
preSum[2 + 1] - preSum[1] + preSum[2 + 1] - preSum[1]
// 等同于
3 - 1 + 3 - 1 = 4
那么到这里你应该自己尝试实现具体的代码逻辑,下面是基于一维数组思路的暴力解法:
/**
* @param {number[][]} matrix
*/
var NumMatrix = function(matrix) {
const preSums = [];
for(let i =0;i<matrix.length;i++){
// 分别求每行数组的前缀和
const preSum = new Array(matrix[i].length + 1);
// 为了让每位元素适用工时,将第0位设置为0是必要的
preSum[0] = 0;
// 套用公式,唯一不同的是数组变成了二维,本质没什么区别
for (let j = 1; j < preSum.length; j++) {
preSum[j] = preSum[j-1]+matrix[i][j-1];
};
preSums.push(preSum);
}
this.preSums = preSums;
};
/**
* @param {number} row1
* @param {number} col1
* @param {number} row2
* @param {number} col2
* @return {number}
*/
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
// 从row1到row2行的前缀和都要加起来
// 每行数组的前缀和符合一维数组前缀和公式,范围其实就是(col1,col2)
// sumRange(i, j) = preSum[j + 1] - preSum[i]
let sum = 0;
for(let i = row1;i<=row2;i++){
sum += this.preSums[i][col2 + 1] - this.preSums[i][col1];
}
return sum;
};
叁 ❀ 二维数组前缀和
前面介绍了比较暴力的做法,现在我们来介绍题目期望我们的做法,也就是套用二维数组前缀和的公式去解答,公式之前没听过不重要,现在你听过了。
我们假设O代表坐标(0,0),D代表坐标(i,j)结合图解,公式如下:
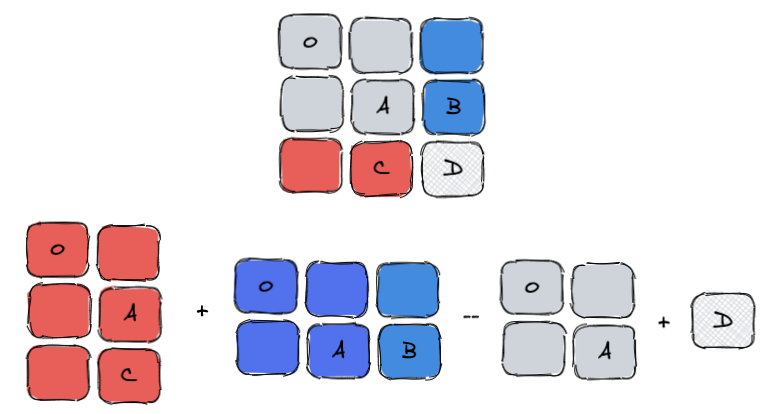
S(O,D)=S(O,C)+S(O,B)−S(O,A)+D
公式的意思是,0-->D的所有元素和,等于0-->C(红色6格)的所有元素和加上O-->B(蓝色6格)的所有元素和,再减去O-->A(灰色4格)的所有元素和,再加一个D(网状格)。
之所以减去一个O-->A是因为O-->C与O-->B两个重复了一次OA,因此得减去。
如果用preSum(i,j)来表示坐标(0,0)到(i,j)的左右元素和,以上公式等同于:
preSum[i][j] = preSum[i][j−1] + preSum[i−1][j] − preSum[i−1][j−1] + matrix[i][j]
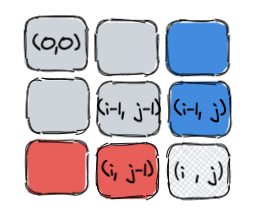
请结合上图来理解,说到底,preSum[i][j−1]就是S(O,C),也就是前面图解中的红色区域,其它同理。而这个matrix[i][j]其实就是题目提供的数组matrix的第i行的第j个元素而已。
在我写这篇文章之前,我当时的第一直觉就是用一个简单的例子来验证这个公式对不对,但比较笨比的是我用了一维数组前缀和累加的思路验证公式,然后苦思冥想了半个小时,心想是不是公式错了...
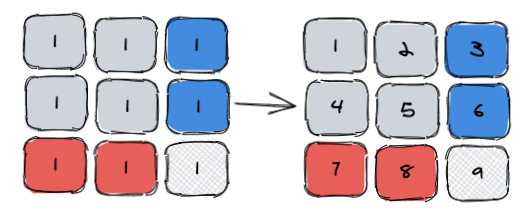
这里的图与一维数组前缀和的图不同在于,之前我们是一行行分别求前缀和,这里我本能的每增一行,都是从上一行最后一个元素的基础上加1作为起点,所以得到了这么个图,那么套入公式:
9 = 8 + 6 - 5 + 1
数学再差的同学也能立马感觉到不对,后面计算出来的数字是10,并不相等。原因其实很简单,我们在前面的图解中也解释过,8这个位置的数字不应该为8,它只应该包含前面图解中O==>C(红色区域)这6个元素,因此应该是6。
所以正确的二维数组前缀和的结果图应该是这样,这里我们直接画出来:
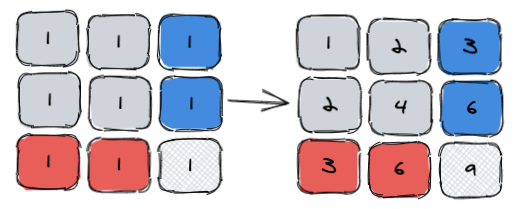
再来验证公式,非常正确:
9 = 6 + 6 - 4 + 1
那么这个二维数组前缀和的这个数字结构要怎么算出来呢?当然是套用我们前面preSum[i][j] = preSum[i][j−1] + preSum[i−1][j] − preSum[i−1][j−1] + matrix[i][j]这个公式算出来的。有同学可能就觉得不对了,以preSum(0,0)为例,它的答案很是1,但很明显我们没办法带入工时,因为不管是i-1还是j-1都超出了数组范围,怎么办?其实还是与一维数组前缀和思路相同,给每行每列都多加一维,且初始值设置为0,如下图:
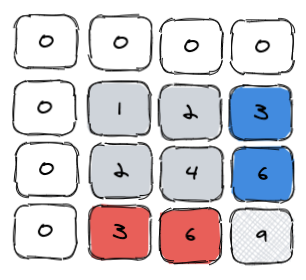
我们再来看preSum(0,0),此时不就是0+0-0+1了么,你看这个公式是不是神了,我们要做的就是给二维数组多加一行一列,并将其都设置为0即可。
我们先来实现第一步,也就是得到一个上图这样的二维数组前缀和,我们可以先预设一个preSum的数组,它的行数应该是数组matrix行数基础加1,列数应该是matrix[i]也就是任意行的列数基础加1:
var NumMatrix = function(matrix) {
// 先创建preSums的行
const preSums = new Array(matrix.length+1);
// 再为每行添加列
for(let i =0; i < preSums.length; i++){
// 注意,这里不能写成 preSums[i] = new Array(matrix[i].length + 1);
// 因为很明显preSums比matrix多一行,i一定会超出matrix的范围,导致报错
// 之所以用0,是因为矩阵中不存在每行列数不同的情况,取第一行为标准就好了
preSums[i] = new Array(matrix[0].length + 1);
}
// 开始套用公式计算二维数组前缀和,同时需要初始化前缀和中第一排以及第一列为0
for(let i = 0; i < preSums.length; i++){
for(let j = 0; j<preSums[i].length; j++){
// 注意,只要是定0行或者第0列,这个格子就应该是0,因此preSums就应该是0
if (i === 0 || j === 0) {
// 只要i是0,不管当前j是多少都应该是0,同理不管第几行,只要j是0也就是第一列,也应该是0
preSums[i][j] = 0
} else {
// 否则就套用公式
preSums[i][j] = preSums[i-1][j] + preSums[i][j-1] - preSums[i-1][j-1] + matrix[i-1][j-1]
}
}
}
// 你可以取消这行注释查看数组结构
// console.log(preSums)
this.preSums = preSums;
};
上面代码的注释真的是我能解释的极限了,所以就不多说啥了,那么到这里我们就套用公式得到了二维数组前缀和的结果,那么这还不够啊,因为题目是要求我们得到矩阵范围区间的和,咋整呢?
我们假设求[[1,1,1],[1,1,1],[1,1,1]]的(0,0,1,1)区间范围和,答案很清楚其实就是4,因为一共四格,问题是怎么算呢?其实还是套用二维数组前缀和公式,为了方便理解,我们还是给出图示:
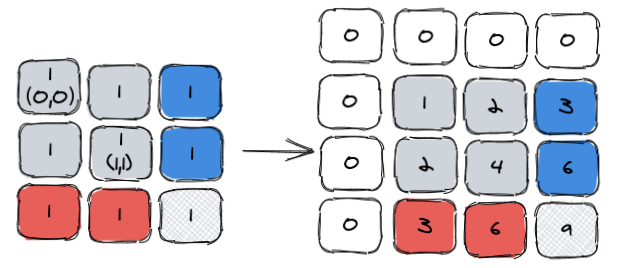
我们将最初的二维数组矩阵对应到右边的前缀和二维数组,要求的和其实还是灰色区域,如果我们还是用区域拆分的方式,你会发现灰色区域等于下图图示:
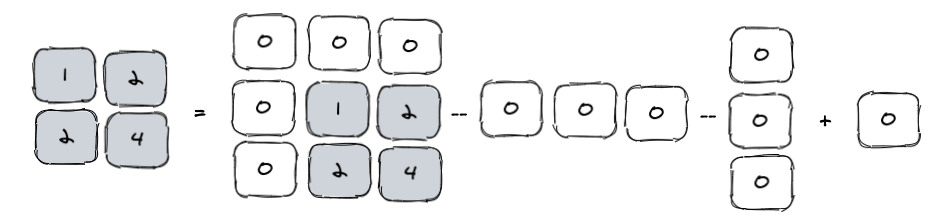
之所以最后要加一个0,也是因为前面减区域时0是交汇处,多减了一次得补回来一个,对应下来其实就是4-0-0+0。为啥横竖三个都是0,我怕大家不理解,其实横着的3个0不就是对应的就是一维数组[0,0,0]的前缀和,竖着的3个0不就是对应二维数组[[0],[0],[0]]的前缀和,所以横竖都是0。
因此满足公式:
preSums(r1,c1,r2,c2) = preSums[r2+1][c2+1] + preSums[r1][c1] - preSums[r1][c2+1] - preSums[r2+1][c1]
为了验证这一点,我们可以假设求数组[[1,1,1],[1,1,1],[1,1,1]]的(1,1,2,2)区间范围和,其实答案也是4,带入公式其实就是9+1-3-3。
如果到这里还不能理解,那建议深呼吸,洗把脸冷静下。
结合上面的代码,最终题解其实就是:
/**
* @param {number[][]} matrix
*/
var NumMatrix = function(matrix) {
// 先创建preSums的行
const preSums = new Array(matrix.length+1);
// 再为每行添加列
for(let i =0; i < preSums.length; i++){
// 注意,这里不能写成 preSums[i] = new Array(matrix[i].length + 1);
// 因为很明显preSums比matrix多一行,i一定会超出matrix的范围,导致报错
// 之所以用0,是因为矩阵中不存在每行列数不同的情况,取第一行为标准就好了
preSums[i] = new Array(matrix[0].length + 1);
}
// 开始套用公式计算二维数组前缀和,同时需要初始化前缀和中第一排以及第一列为0
for(let i = 0; i < preSums.length; i++){
for(let j = 0; j<preSums[i].length; j++){
// 注意,只要是定0行或者第0列,这个格子就应该是0,因此preSums就应该是0
if (i === 0 || j === 0) {
// 只要i是0,不管当前j是多少都应该是0,同理不管第几行,只要j是0也就是第一列,也应该是0
preSums[i][j] = 0
} else {
// 否则就套用公式
preSums[i][j] = preSums[i-1][j] + preSums[i][j-1] - preSums[i-1][j-1] + matrix[i-1][j-1]
}
}
}
// 你可以取消这行注释查看数组结构
// console.log(preSums)
this.preSums = preSums;
};
/**
* @param {number} row1
* @param {number} col1
* @param {number} row2
* @param {number} col2
* @return {number}
*/
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
return this.preSums[row2+1][col2+1] + this.preSums[row1][col1] - this.preSums[row1][col2+1] - this.preSums[row2+1][col1]
};
你说发现长篇大论下来,围绕的还是一个二维数组求前缀和的公式展开,可能你会觉得,我要是不知道这个公式鬼做的出来,但不管怎么说,你现在知道了这个公式,就像我们以前不知道1+1=2一样,现在知道了,以后也就知道了。如果时间久了再遇到此题,我们还是可以从最简单的九宫格开始,九个格子都是1,标好ABCDO四个点,按照区域划分的思维去推导此公式。
我现在其实挺不乐意去记录这种复杂的算法题解,比如这篇文章,从理解画图到写作,前前后后用了快5个小时,LeetCode中存在上千道这样的题目,如果记录我还要用多少时间呢?可是后来一想,我不去做,不去写,可能永远都不懂这个题目的思路,不管怎么样算是把这道题啃下来了,有收获就好,哪怕一点点。
那么到这里本文结束。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号