JS LeetCode 303. 区域和检索 - 数组不可变,一维数组的前缀和
壹 ❀ 引
本题来自LeetCode303. 区域和检索 - 数组不可变,属于一道简单题,不过题目期望的做法我也是看了题解才懂得,这里大致做个记录,题目描述如下:
给定一个整数数组 nums,求出数组从索引 i 到 j(i ≤ j)范围内元素的总和,包含 i、j 两点。
实现 NumArray 类:
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 从索引 i 到 j(i ≤ j)范围内元素的总和,包含 i、j 两点(也就是 sum(nums[i], nums[i + 1], ... , nums[j]))示例:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]输出:
[null, 1, -1, -3]解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]); numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3) numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))提示:
0 <= nums.length <= 104
-105 <= nums[i] <= 105
0 <= i <= j < nums.length
最多调用 104 次 sumRange 方法
贰 ❀ 简单分析与暴力题解
题目其实不难理解,我们需要定义一个类NumArray,它接受一个数组nums作为初始化对象,然后调用此类的sumRange方法并传递两个参数i与j,并求出nums中索引i到索引j(i<=j且包含i与j)之间所有元素的和。
不用看官方给的例子,它给的输入看着有点莫名其妙,说直接点就是,假设我们有个数组[1,2,3,4]作为初始化参数,那么调用sumRange(1,3),得到的就是9,因为索引1是2,到索引3是4,中间还有个3,因此和为2+3+4。
站在JS角度,这里我直接使用构造函数模拟这个类,因为暴力解法非常简单,这里直接贴代码:
/**
* @param {number[]} nums
*/
var NumArray = function(nums) {
this.nums = nums;
};
/**
* @param {number} i
* @param {number} j
* @return {number}
*/
NumArray.prototype.sumRange = function(i, j) {
let sum = 0;
while(i<=j){
sum+=this.nums[i++]
};
return sum;
};
在上述代码中,NumArray接受一个函数作为参数,之后调用sumRange时,我们也只需要通过遍历,将从i到j的所有数字累加,并最终返回结果即可。
叁 ❀ 前缀和
但事实上,如果你没了解过前缀和的概念,你可能完全不会想到此题的真正考点是希望你用前缀和来解决此问题。
站在暴力解法的角度,我们每调用一次sumRange其实都得从头开始把范围内的数字都重新加一半,这种行为是不具备缓存性质的。那么有没有什么办法,能够让我们在调用sumRange时不用做重复的工作,而是直接得到结果呢,这里就得介绍前缀和了。
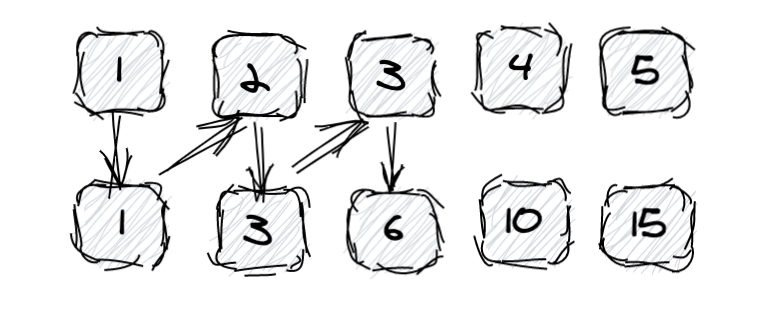
也不卖关子,我们以一个数组[1,2,3,4,5]为例,所谓前缀和其实就是第i项保存了包含i以及i之前所有元素的和。
我们假设有个专门的数组用于存放前缀和,它的结果应该是这样:
元素: 1,2,3,4,5
前缀和:1,3,6,10,15
第一个前缀和为1,这是因为目前只有一个,因此为1。
第二个前缀和为3,这是因为2前面还有一个1,因此为1+2=3
第三个前缀和为6,这是因为1+2+3=6,但是我们之前已经计算过1+2了,因此我们可以用上次的前缀和加上当前元素就好了,简化为3+3。
以此类推,假设前缀和的数组为preSum,那么:
preSum[i] = preSum[i-1] + nums[i]
我们期望上面的公式能适用于数组遍历的整个过程,但很明显当索引为0时,此时只有一个元素1,都不存在preSum[i-1],怎么办呢?聪明的前辈们想到了一个机智的做法,nums不是长度为5吗,那我的preSum初始化时长度就在nums长度基础上加个1也就是6,并将preSum[0]直接设置为0,也就是:
let preSum = new Array(nums.length);
preSum[0] = 0;
直接让pre多出一个,并将其设置为0,方便后续每一次的前缀和计算,简直妙哉。因此我们可以在第一次遍历数组时,就得到对应的前缀和数组,上代码:
var NumArray = function (nums) {
// 我需要一个length+1的数组,用于保存前缀和
const preSum = new Array(nums.length + 1);
// 为了让前缀和的公式适用于数组每一位计算,所以将0位的值设置为0
preSum[0] = 0;
// 虽然公式是pre[i] = pre[i-1] + nums[i],但是索引是从0开始的,因此preSum的第一位应该是i+1
for (let i = 0; i < nums.length; i++) {
preSum[i + 1] = preSum[i] + nums[i];
}
this.preSum = preSum;
};
OK,那么到这里我们得到了一个前缀和数组,但题目的目的是调用sumRange(i,j)时能得到次区间的和,怎么办呢?
还是举个简单的例子,以数组[1,2,3,4,5]为例,求假设i为1,j为3,求i-j区间的和。
首先0-3的和为1+2+3+4,而1-3的和为2+3+4,因此可以得知,1-3的和可以是0-3的和减去一个1,也就是减去一个preSum[i-1]。
但由于我们在声明preSum时长度加了个1,因此从要跟nums的下标对应的话,我们在计算时,公式应该为:
sumRange(i, j) = preSum[j + 1] - preSum[i]
还是上面的数组例子,假设要求1-3的区间和,很明显应该是10-1=9,说到底就是初始值0的问题,要让j加一位,这样计算才是正确的。
元素: 1,2,3,4,5
前缀和:0,1,3,6,10,15
综合上述代码,可以以前缀和的思路得到最终代码:
var NumArray = function (nums) {
// 我需要一个length+1的数组,用于保存前缀和
const preSum = new Array(nums.length + 1);
// 为了让前缀和的公式适用于数组每一位计算,所以将0位的值设置为0
preSum[0] = 0;
// 虽然公式是pre[i] = pre[i-1] + nums[i],但是索引是从0开始的,因此preSum的第一位应该是i+1
for (let i = 0; i < nums.length; i++) {
preSum[i + 1] = preSum[i] + nums[i];
}
this.preSum = preSum;
};
NumArray.prototype.sumRange = function (i, j) {
return this.preSum[j + 1] - this.preSum[i];
};
这样每次查询区间和时,我们都能利用之前遍历缓存的前缀和高效得到最终结果,大功告成,本文结束。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号