从零开始的算法入门科普（二），你应该知道的数据结构类型·其二

壹 ❀ 引

我在从零开始的算法入门科普（一）这篇文章中，简述了数据结构与算法的联系，好的数据结构设计会让算法工作事半功倍。那么在这篇文章中，我们接着以图示的形式将其它数据结构一一说完，废话不多说，本文开始。

贰 ❀ 数据类型

贰 ✿ 壹 栈Stack

栈也是数据结构的一种，需要注意的是栈只能在固定端进行数据插入与删除，先插入的数据总是被压入栈底，最后插入的数据在栈顶。

比如上图中，最先插入的数据Green被压入栈底，随着数据的不断插入，如果想取出Green，我们得先取出Red再取出Blue。

所以栈满足后进先出（LIFO）的特点，虽然当我们想取栈中数据首先得先取出上层数据，但是站在如果我们总是要取最新数据的角度，栈无疑非常有优势。

在JavaScript开发中，函数调用，执行上下文与递归等，都会使用栈。

贰 ✿ 壹 队列Queue

队列与前面介绍的几种数据相同，都是排成一列的数据结构。队列与栈尤为类似，但和栈不同的是，队列有队头和队尾，插入数据在队尾，删除数据在队头。

比如上面的例子中，先插入的Green在取出时也是第一位，因此队列满足先进先出（FIFO）的条件。

贰 ✿ 壹 哈希表Hash table

哈希表又称为散列表，是一种借助哈希函数进行数据存储与读取的数据结构，哈希表一般用于存储键值对（key-value）数据。

简单解释下概念，假设现在存在键key，我们将key带入哈希函数f()，从而得到用于存放与key对应的value的地址信息。而下次我们要访问value时，还是通过哈希函数f(key)得到存储地址信息，以便快速访问数据。

那么，什么是哈希函数呢？哈希函数其实就是把输入的数据转换成固定长度的不规则的值的函数，这个值也称为哈希code。

当然，我们在这里不会介绍怎么实现哈希函数，现有的哈希函数算法有多种，比如代表性的MD5，SHA-1，SHA-2等等。

介绍完哈希函数，我们还是回过头来介绍哈希表，我们来通过一个例子加深印象。

假设现在我们有多个姓名与性别的键值对，其中key为姓名，性别为value，我们要做的就是已知某个名字，能快速查找出该名字的用户性别。

如果我们使用之前介绍的数组来存放数组，那么应该是下图这样：

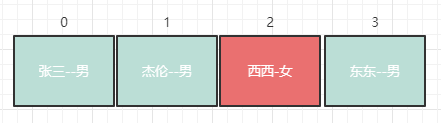
现在我们要知道西西的性别，由于不知道在数组第几位，所以只能进行线性搜索，一直找到第三位发现用户为西西，从而得到性别为女。

利用数组存储的问题是，随着数据越来越大，我们查找耗时也会更大，如果刚好要找的用户是最后一位，那就得将整个数组遍历一遍，有没有更好的做法呢，比如使用哈希表。

假设现在我们已实现了一个哈希函数f()，已有一个包含四个不同地址的空哈希表。

现在我们将张三带入哈希函数计算得到位置1，即f('张三')=>1于是我们将张三的数据存到哈希表1的位置：

之后分别带入西西，东东，得到不同地址f('西西')=>2，f('东东')=>3，我们存入哈希表中对应位置：

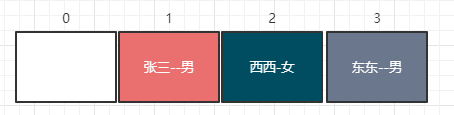
很不巧，当我们带入杰伦进行计算时，得到的位置信息也是1，像f('张三')=f('杰伦')这样的情况，有个专业名词叫冲突，而杰伦的数据将采用链表指针的形式紧跟张三之后，像这样：

好了，现在我们要知道西西的性别，通过f('西西')=>2，我们直接去哈希表中位置为2的地方找，于是顺利得知西西性别为女。而假设我们现在要找杰伦，因为f('杰伦')=>1，于是看位置为1的地方，即便第一个为张三，但我们还是很快定位到第二个数据即是我们想要答案，你看，即便是这样也要比最初数据排列要更快。

哈希表因为哈希函数的作用，能在存放数据后快速读取，即便发生了冲突，我们也可以通过链表将冲突数据相连。但需要注意的是，如果哈希表的哈希值范围过小，容易造成大量冲突，这也会带来与数组一样的遍历麻烦；反之，如果哈希值范围给的过大，就会造成上述我们模拟例子中未存放数据的空地址，所以选定哈希值范围也格外重要。

贰 ✿ 壹 堆Heap

堆通常可以看成是一颗完全二叉树的数组对象，因为属于二叉树范畴，所以堆也是图形的树状结构之一。堆总是满足两个条件。一是堆中某个节点的值总是不大于或不小于其父节点的值，二是堆总是一颗完全二叉树。

完全二叉树：当二叉树的深度为k时，它的k层节点必须都是连续靠左并不可隔开的，并且1～k-1层的结点数都达到最大个数(即1~k-1层为一个满二叉树)。

为了方便展示，我们下方例子都使用根节点最小的堆，即每个节点必定大于自己的父节点，这种堆也称为最小堆或小根堆。一个理想的小根堆如下图：

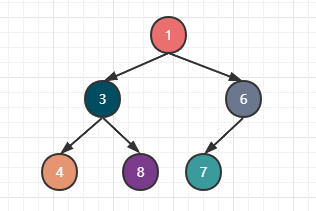
可以看到上图满足完全二叉树的情况，其次每个节点都比自己的父节点大。

另外还做个补充，二叉树除了完全二叉树（上面给的例子）还有满二叉树，所谓满二叉树即是：

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。如果二叉树的层数为k，那么节点总数就是(2^k)-1个，这就是满二叉树。

上图例子就是一个满二叉树，可以看到满二叉树都是一个规则的三角形。

堆一般用于实现优先级队列（priority queue），有同学就疑惑了，这堆还没说清楚，怎么又来了个优先级队列，我们先给个优先级队列的概念，引用百度：

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

OK，现在我们通过一个例子来理解优先级队列和堆数据存储与获取过程。

假设有下图一个小根堆，我们要在堆中添加一个为5的子节点。

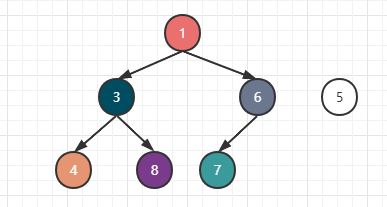
由于在子节点6的下方有空缺，所以5先被放在这里。

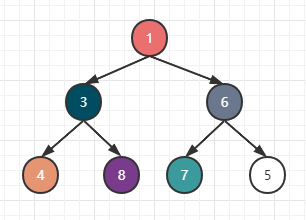
但前面我们说了，小根堆的子节点都应该比父节点大，所以5和6应该互换位置，如下：

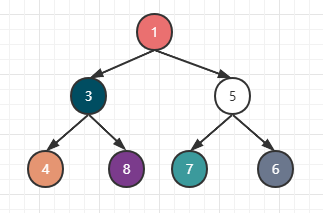
接着对比5和1，由于子节点5比父节点1大，所以无需调换位置。

现在我们说说堆取数据，堆中获取数据满足从最上层开始，并为之最上面的数永远最小，比如现在我们将1取走。

由于最小数的位置空缺，所以现在要重新整理堆的解构，堆的规则就是将最后的数移动到最上方，所以6被移动到了最上层：

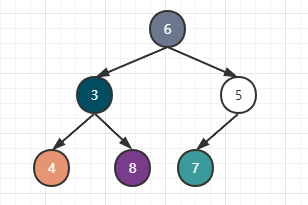
问题又来了，我们还是得满足子节点要大于父节点的规则，堆再次进行整理，但问题是子节点3与子节点5都比6要小，这时候堆会选择子节点中更小的一个与父节点互换，所以最后是3与6互换，如下：

换完之后，子节点4又比6小，所以再次互换，如下：

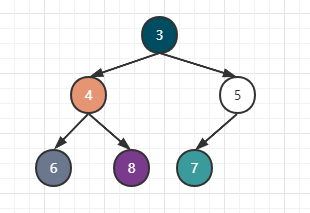
一直到这里，我们取一个数据的操作就算完成了，是不是有点麻烦，但堆也有它的优势。

以小根堆为例，堆最上方的值永远是最小数据，所以取出最小值的实际为O(1)。此外，取出数据重新排列结构时，必须将最尾端的数据提到最上面，然后再进行拍讯，所以排列执行时间与树状结构层级成正比。

假设节点个数为n，那么可知层数为log2n，重新整理堆的耗时为O(logn)。追加数据也需要作比较，同理也得反复跟父级做大小对比，以达到子节点大于父节点的条件，所以追加时整理耗时也为O(logn)。

综合来说，如果总是要从数据结构中取最大或最小值，小根堆或者大根堆是不错的选择。

贰 ✿ 壹 二叉搜索树Binary search tree

二叉搜索树也是树状结构一种，它的一大特点是每个节点最多有2个子节点。除此之外二叉搜索树具备如下特别，同时若树的左子树不为空，那么左子树的节点均大于连接在左边的任意子节点；若右子树不为空，那么右子树的节点均小于连接在右边的任意子节点。读起来有点绕口，我们来看个例子（偷个懒，不加颜色了）：

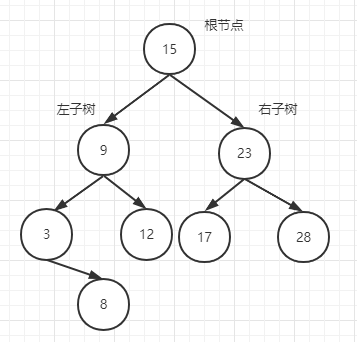
如上图，节点9的左子树的任意节点均比9小，再往上看，节点15的左子树的节点有9,3,8,12都比15小。我们再看第二特征，节点15的右子树节点有23,17,28，他们都比15要大，就这么个意思。

通过这个特征我们不难得出，从根节点往左子树看，只看左子树分支，最尾端的一定是最小数，也就是3。而从根节点往右子树看，位于右子树分支的最尾端一定是最大数，也就是28。

接着我们说说二叉搜索树添加节点的过程，比如我们要追加一个节点1，由于1比15小，所以它得往左子树下面移动。

在跟9比较之后因为比9小，所以继续往9的左分支下移，再跟3比较，最后添加到了3的左分支

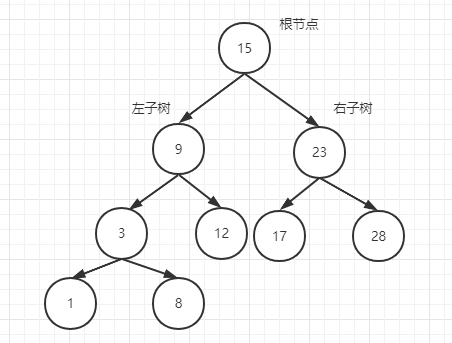
而当我们要查找某个节点时，原理其实与插入节点一样，查找的目标会以此与节点进行对比，直到找到对应的节点，这里就不再说过多描述。

最后说说二叉搜索树删除，比如还是我们上面添加节点1之后的解构，现在把节点9给删除。

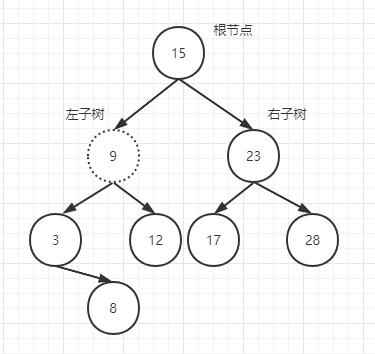
还记得二叉搜索树的两大特诊吗，节点9被删除后，后续工作就是从节点9的左子树分支中找到最大数拿过去替补，这里就是节点8，所以如下：

你看，8比左子树的3大，比右子树的12小，同时比父节点15小。

二叉搜索树在查找的特点就是将目标与当前节点做比较，来决定是往左还是往右查找，二叉搜索树比较次数与层级数有关，毕竟有几层就得一直比较到底。当有n个节点，树状结构达到满二叉树的结构，最多只需要进行log2n次的比较和移动即可，所以耗时为O(logn)。而如果n个节点被排成一条分支，也就是一条直线，那就得从头找到尾，时间复杂度为O(n)。

叁 ❀ 总

比较曲折，还是花了大半天的时间将剩余数据结构图解讲完了，其实有点后悔开了这个坑，最大的问题在于，我写博客的时间甚至达到我学习这部分只是时间的三四倍，画图真的太累了...

所以后续我还是先保证自己能把知识学完，至于后续博客，尽力更新，那么到这里本文结束！