从零开始的算法入门科普（一），你应该知道的数据结构类型·其一

壹 ❀ 引

算法，对于大多数开发者而言，是一个既陌生又熟悉的词汇。陌生在于它很高格调，学好算法似乎很难；而熟悉在于，开发中的一次排序，一次查找甚至一次计算都与算法脱不开关系。

不可否认，不管你使用的是哪种开发语言，学好算法是成为高级开发的必经之路。而像博主这种非计算机专业出身，大学没学过数学的人而言，学算法尤为痛苦（苦笑）...

我之前打算通过刷LeetCode来提升算法能力，但因为缺乏算法基础知识，啃得过慢。如果你有关注过我的博客更新，就能发现我之前有写过三篇排序文章，很尴尬，写了忘忘了写反复之间我选择暂停刷题。

最近我从公司借了一本不错的算法入门图书《演算法图鉴》，大致翻阅，本书主要围绕数据结构，排序，查找，安全算法等几个章节展开，图解的形式非常适合我这种小白。所以我打算花半个月左右时间将本书啃完，而这片文章算是我读此书的开端。

2020.6.5更新，微信读书已更新《演算法图鉴》电子版，对于算法0基础小白强烈推荐，无任何代码全部以图文展示--我的第一本算法书

学习不是一两天，算法提升也是如此。有志者事竟成，愿你我都能在算法上勇敢跨出第一步，那么本文开始。

贰 ❀ 算法与数据结构

数据结构（data structure）用于决定数据的存放顺序与位置。有同学肯定纳闷，说算法怎么又扯到数据结构了，让我们通过一个例子来解释算法与数据结构的紧密关系。

假设我们现在需要存储一些用户的电话号码，信息就包括用户名与用户的手机号码，我们首先想到的自然是如下结构：

姓名	电话号码
张三	136****1734
李四	130****3312
王五	130****7213
李星星	135****1535
西西	173****9797

这样存储其实没问题，如果再有新增，我们只需在结尾再加一行即可。好了，现在我们要查询王五的电话号码，由于存储并无规则，所以我们只能从头到尾查一遍，或者随机性的查阅，运气好一眼看到了。但如果数量过大，可能这个运气就很难好起来了。

如何改进？有同学立马想到手机通讯录存储方式，按照姓名首字母排序，这样很棒，如下：

姓名	电话号码
(L)李四	130****3312
(L)李星星	135****1535
(W)王五	130****7213
(X)西西	173****9797
(Z)张三	136****1734

现在要找到王五就非常简单了，只要熟悉字母表顺序，扫一眼就能快速定位到W开头的姓氏，大大降低了查找难度。可问题又来了，现在要新增一条用户数据汪伦，由于也属于W开头，所以得紧跟王五之后，但由于没了空间，所以我们只能将西西与张三统一往后挪腾出空间，假设这个行为都是我们手动完成，想想就觉得麻烦。

还能再改进吗？让我们回顾上面两种存储方式，方式一查找麻烦但是新增方便，方式二查找方便但是新增麻烦，那要不我们将两种方式结合下？如下：

姓名(L)	电话号码
李四	130****3312
李星星	135****1535

姓名(W)	电话号码
王五	130****7213
汪伦	130****3312

姓名(X)	电话号码
西西	173****9797

姓名(Z)	电话号码
张三	136****1734

现在我们将不同字母开头的姓氏分别存在不同的表中，这样查找和新增都非常方便了。你看，我们先不谈算法，好的数据结构本质上就能大大提升算法效率，所以了解常见的数据结构很有必要。

叁 ❀ 常见数据结构类型

叁 ✿ 壹 链表List

链表是数据结构中的一种，这类结构的数据排成一条直线，便于查找和删除，但存放数据比较费时。链表往往由数据和指针构成：

这是一个理想中的链表结构，每个数据都有指针指向下一个数据所在的位置。实际存储可能没有这么乖巧，因为有指针起到指向作用，因此即便数据分散开来也不影响链表存储数据。

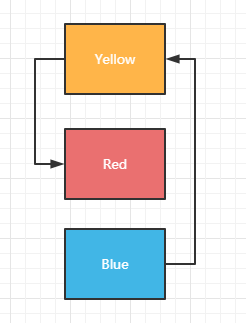
链表一大特点就是查找某个数据时，必须按照指针依次读取数据，比如上图中想要找到Red，必须先找到Blue再找到Yellow依次查找才行。

链表结构追加数据时，要做的就是将插入数据前的指针指向自己，并将新数据的指针指向原本紧接的数据即可，比如现在我们在Yellow与Red之间新增一个Purple：

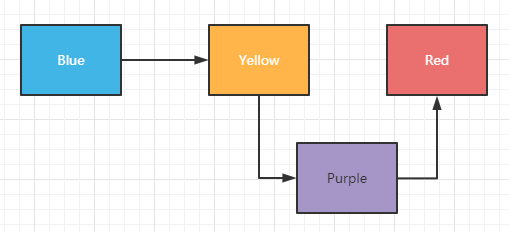
假设我们现在要删除Purple数据也很简单，将Yellow指向Purple的指针指向Red即可：

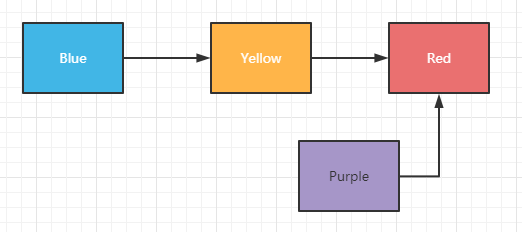
虽然图解上来看，Purple还有指针指向Red数据，但实际Purple已经变成了无法读取的数据。

以上链表一大特点是作为数据结尾的Red并无指针，有没有Red也有指针的情况呢？有，比如循环链表（circular list），循环链表并没有头尾的概念，每个数据都扮演着头尾的角色。

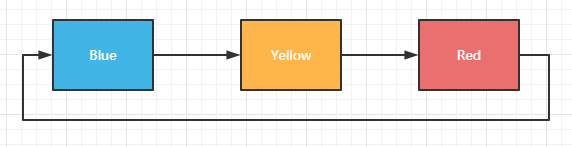
除此之外，上面的链表数据都只有一个指针，事实上也存在两个指针的情况，也就是双向链表（bidirectional list），双向链表的特点就是没有前后之分，从数据读取上来说比单向更方便，缺点是如果要新增数据或者删除时，需要修改的指针会大大增多：

链表在查找上由于需要从头开始找，数量越多查找时间越长，所以查找执行时间与数据个数n有关，因此查找时间为O(n)，而新增数据时只需要修改制定的箭头指向，这与数据个数无关，因此修改数据的执行时间为O(1)。

叁 ✿ 贰 数组Array

数组也是数据结构的一种，像我这种前端开发，与数组打交道的次数就多到数不清。数组结构的数据在追加数据以及读取时会非常便利，但在插入数据以及删除数据会耗时耗力。一个理想的数组结构如下：

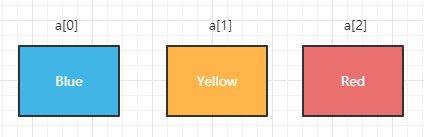
上图展示的其实就是一个包含了Blue、Yellow、Red三个字符串的数组a。数组中的数据具有连续性，所以我们可以通过索引访问指定位置的数据。比如现在要找到Red链表得从头开始查，而数组只用通过索引a[2]即可访问，非常方便。

数组虽然查很便利，但如果要在数组中插入或删除某个元素就会比链表逊色很多，比如我们要在Bule和Yellow中间插入Purple，如下图：

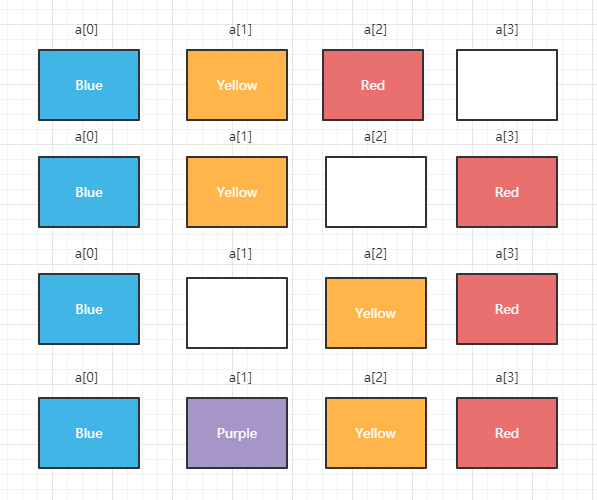
首先数组中会新建追加数据的空间，之后依次将数据往后移动，直到将Blue后的空间腾出来，然后将Purple放进去，这就是一次数组的插入；同理，当我们要删除Purple时，又得将Purple之后的数据往前挪，直到填补上前面的空缺，所以对比起来数组在中间插入与删除上确实比链表要麻烦的多。

前面我们说了数组查询可依赖索引，查询时间与数组元素个数无关，所以查询耗时为O(1)，而修改数组，比如新增删除，按照时间复杂度最坏的来计算，假设是在第一位前新增元素，或者删除第一位元素，要做的操作就会受到数组元素个数n的影响，所以操作的时间复杂度为O(n)。

肆 ❀ 总

那么到这里，我们介绍数据类型中的链表与数组两种数据，当然数据类型远远不止这两种，因为时间问题（明天还要上班），后面的几种类型我会在第二篇中介绍。

回顾上文，我们来将两种数据结构做个对比：

	读取	新增	删除
链表	慢 O(n)	快 O(1)	快 O(1)
数组	快 O(1)	慢 O(n)	慢 O(n)

你看，不同数据结构在不同操作上表现会完全不同，以数组和链表为例，如果我们希望数据知识单独访问，很明显数组更为方便，而如果数组要频繁操作，链表就更具优势了，这就是数据结构的魅力。

由于本文记录过程中画图确实有点费时，后续的数据结构我会在第二篇中介绍，加油加油，那么本文到这里正式结束。