js 为何范围内随机取整要用floor，而不是ceil或者round呢

 壹 ❀ 引

我在如何使用js取任意范围内随机整数这篇博客中，列举并分析了取[n,m)与[n,m]范围内整数的通用方法，并在文章结果留了一个疑问；为什么通用方法中取整操作，我们使用Math.floor()而不是Math.ceil()或者Math.round()方法呢？

知其然更知其所以然，加上在GitHub中那道笔试题答案下，不少网友的答案使用了round或ceil方法来取整，说明不少人对于随机取整为何一定要用floor方法是没有一个深刻理解的，那么本文就对于这个问题展开分析。

 贰 ❀ round ceil floor有何区别

在弄懂这个问题前，我们先将这三个方法的区别说清楚，它们都是JavaScript提供的数字取整方法，但却有着本质区别。

1.关于Math.round()

Math.round()的含义是将一个数字四舍五入为最接近的整数，四舍五入大家不会陌生，一个数字如果是4那就舍弃掉，如果是5，那就进一。

Math.round(0.5); //1
Math.round(1.2); //1
Math.round(2.41); //2
Math.round(-3.55); //-4

2.关于Math.ceil()

Math.ceil()的含义是向上取整，说直白点，就是得到一个大于等于且最接近自己的整数，不难理解。

Math.ceil(0); //0
Math.ceil(1.2); //2
Math.ceil(2.41); //3
Math.ceil(-3.55); //-3

3.关于Math.floor()

Math.floor()刚好与Math.ceil()相反，这是一对冤家，它表示的是向下取整，也就是找小于等于且最接近自己的整数。

Math.floor(0); //0
Math.floor(1.2); //1
Math.floor(2.41); //2
Math.floor(-3.55); //-4

 叁 ❀ 随机整数概率问题

1.使用round的问题

我们知道，当取[0,5]范围内随机整数时，从概率角度，我们是希望每个随机数出现概率是相同的，那么当我们使用round方法会有什么问题呢？

round的作用是四舍五入取整，为了不那么复杂，我们将数字范围划分为0 -- 0.5 -- 1 -- 1.5 -- 2 -- 2.5 -- 3 -- 3.5 -- 4 -- 4.5 -- 5 这几个阶段。

很明显，当范围是0 -- 0.499之前被四舍五入为0，而0.5 -- 1与1 -- 1.4999可四舍五入为1，同理，2阶段，3阶段，4阶段都是前后两个范围，4.5 -- 5可四舍五入为5。

由此可以统计出1，2，3，4出现的概率要整整比0，5两个边界数字出现的概率高百分之50，我们做个简单的测试：

Math.floor(Math.random() * 6);

这段代码，是取[0,5]范围的随机整数，我们将floor改为round，简单修改逻辑(因为四舍五入，这里改为乘以5)，查看每五次取得数字的概率：

function randomArr() {
    let arr = [],
        length = 5;
    while (length--) {
        arr.push(Math.round(Math.random() * 5));
    };
    console.log(arr);
};
setInterval(function () {
    randomArr();
}, 1000);

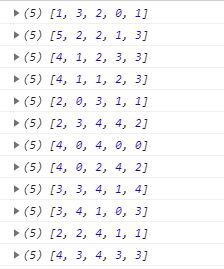
如上图，一眼扫下来出现0与5的概率，普遍比1,2,3,4要低，很明显这对于0与5两个边界数字是不公平的。

2.使用ceil取整的问题

有了上面的分析，ceil就好理解多了，同样是[0,5]范围取随机整数，我看同样做范围拆分。

由于是ceil是向上取整，只有是0时，才是0；只要超过0，0.1甚至0.0001都会向上取整变成1,同理，2，3，4，5概率都会相同，我们可以得出使用ceil对于0是极不公平的，我们将上面的代码中的round改为ceil：

想要随机取整的数字是0的概率，简直比中彩票头等奖还低，毕竟0-1范围内的随机数字组合可以说无数个，外加上还有2,3,4,5几个数字，这下总知道为啥不能用ceil了吧。

3.使用floor为什么可以

floor因为是向下取整，0-0.999之前都是0，1-1.999之前都是1，每个数字概率相同。

所以我们取[0-5]范围内整数时，使用的是Math.random() * 6，得到的范围就是[0-5.999..]，在通过下下取整，也就达到取[0-5]的目的了。

4.使用ceil取整后减去1模拟floor？

不对啊，向下取整概率相同，我向上取整不也一样？求[0-5]范围时，我能不能利用向上取整，求一个[1-6]再减去1呢？很明显不行。

0.1-0.999向上取整是1，1.1-1.999向上取整是2，我们这个基础上减去一个1，想法是好的，但这个想法忽略了比中彩票还难出现的数字0，只要0出现，我们根据通用想法减去1，那就是-1了。

Math.ceil(Math.random() * 6) - 1

这段代码貌似能正常取到0-5范围的任意整数，其实当0出现时，就BUG了，虽然我们不知道0什么时候会出现。

 肆 ❀ 总

那么文章到这，我们大概知道了这几个知识点：

1.round floor ceil的作用与区别

2.为什么取范围随机整数使用floor而不是round或者ceil

3.利用floor的思想模拟了ceil减一的做法，结果行不通

那么到这，算是给文章开头的问题解答疑惑了，现在你知道为什么不能使用round或者ceil取随机整数了吗？