PTA的Python练习题（十一）

从 第4章-3 猴子吃桃问题 继续

1.

 

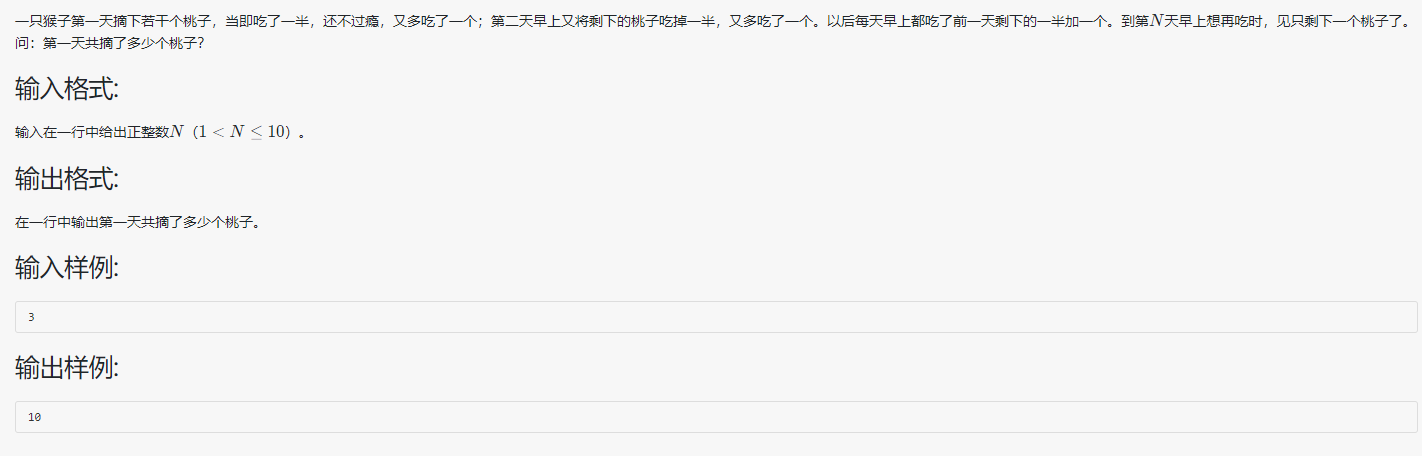
a=eval(input())
def count(n):
    b=1
    for i in range(n-1):
        b=(b+1)*2
    return b
print(count(a))

 

2.

这道题让我们验证哥德巴赫猜想

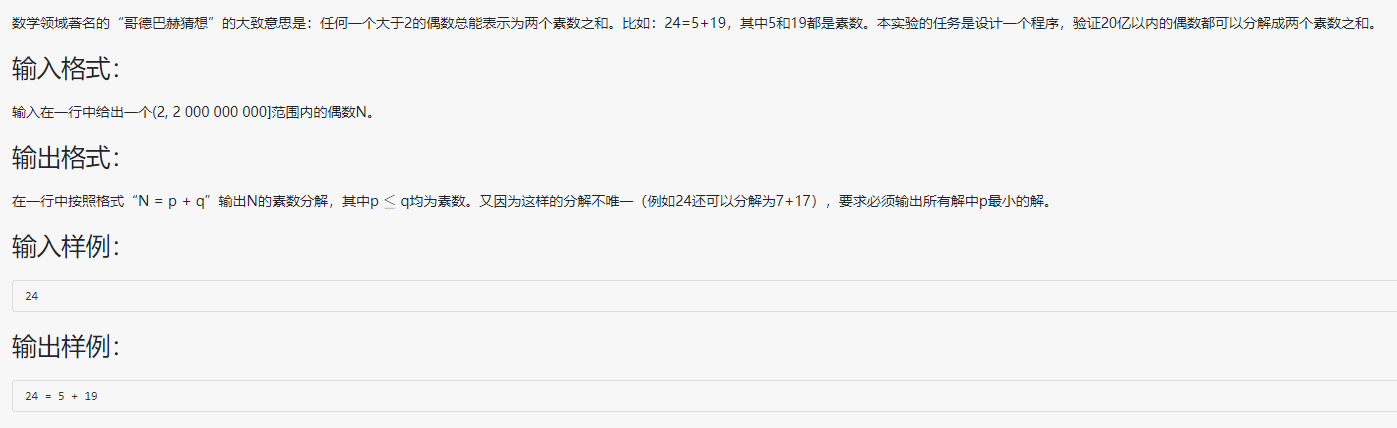
没什么思路，参考了别人的代码：

思路：定义一个判断素数的函数，然后再用两数相加和不变，判断最小的解和另一个解是否为素数

知识点：

import math
def isPrime(n):
  if n <= 1:
    return False
  for i in range(2, int(math.sqrt(n)) + 1):
    if n % i == 0:
        return False
  return True
x=int(input())
for y in range(2,x//2+1):
    z = x - y
    if (isPrime(y) == 1 and isPrime(z) == 1):
        print('{:d} = {:d} + {:d}'.format(x, y, z))
        break

 

3.

a=eval(input())
def count(n):
    b=1
    c=1
    d=1
    for i in range(2,n+2):
        b=b+1/c
        d = d + 1
        c=c*d
    return b
print('%.8f'%(count(a)))