machine learning 之 Neural Network 2

整理自Andrew Ng的machine learning 课程 week5.

Neural network and classification
Cost function
Backpropagation （to minimize cost function）
Backpropagation in practice
Gradient checking
Random initialization
Assure structure and Train a neural network

前提：

训练数据集： ${(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}$

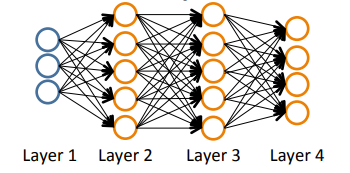
L：神经网络的总的层数，total layers，如下图，L=4

$s_l$ ：第l层的单元数目，如下图， $s_1=3, s_2=5,...$

K：输出层的单元数，如下图，K=4

1、neural network and classification

对于二分类问题（binary classification）：输出为0或1，K=1

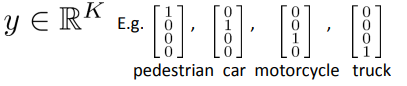
对于多分类问题（Multi-class classification）：输出为hot one编码形式，K为类别数目，类似如下：

2、cost function

之前的文章中介绍过logistic regression的cost function为：

$J(\theta)=-\frac{1}{m}[\sum_{i=1}^m y^{(i)}logh_\theta(x^{(i)}) + (1-y^{(i)})log(1-h_\theta(x{(i)}))] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2$

more generally，在神经网络中， $h_\Theta(x) \in R^K，(h_\Theta(x))_i是第i个output$ ，神经网络的cost function为：

$J(\Theta)=-\frac{1}{m}[\sum_{i=1}^m \sum_{k=1}^K y_k^{(i)}log(h_\Theta(x^{(i)})_k) + (1-y_k^{(i)})log(1-(h_\Theta(x{(i)}))_k)] + \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} (\Theta_{ji}^{(l)})^2$

相比于logistic regression：

需要把K个输出的损失相加，所以有了K个累加项；
在惩罚项里面，需要把除bias unit以外的所有的参数（除 $\Theta_0以外的所有\Theta$ ）都进行惩罚；

3、Backpropagation

有了cost function之后，我们就需要minimize cost function，使用的就是backpropagation算法计算出进行参数更新的值（类似于梯度下降的偏导数），也就是神经网络的损失函数的偏导数：

梯度计算：

首先进行forward propagation，计算出每一层的单元值（包括输出层的值）；（上一篇文章的内容）
进行backpropagation：（以前提中的神经网络为例）
- 设定 $\delta_k^{(l)}$ ：为第l层上第j个结点的误差error，那么 $\delta_j^{(4)}=a_j^{(4)}-y_j$ ，给出 $\delta^{(l)}=(\theta^{(l)})^T\delta^{(l+1)}.*g^{'}(z^{(l)})$ ，其中 $g^{'}(z^{(l)})=a^{(l)}.*(1-a^{(l)})$
- 给出公式 $\frac{\partial J(\theta)}{\partial \theta_{ij}^{(l)}}=a_j^{(l)}\delta_i^{(l+1)}$
- 对于每一个训练数据，计算它们的偏导数，并且将其相加， $\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T$
- 在所有的训练数据处理完之后，计算损失函数对每一个参数的偏导数，也就是参数的更新参数， $D_{ij}^{(l)}=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}$ ，当j为0时， $\lambda$ 为0（ $\theta_0$ 不惩罚）

4、Backpropagation in practice

unrolling parameters：把矩阵形式的参数展开成向量，为了使用已有的函数对损失函数进行最小化运算；（matrix to vector）

reshape：vector to matrix，在计算偏导数和损失函数时，矩阵运算

5、Gradient checking

做了backpropagation计算了损失函数对每个参数的偏导数之后，我们需要做一个checking来确定偏导数的计算是否正确，数值计算梯度如图所示：

计算公式为：（ $\varepsilon$ 取一个很小的值，领域的概念）

$\frac{J(\theta+\varepsilon)-J(\theta-\varepsilon)}{2\varepsilon}$

对于所有的参数，数值计算偏导数的公式如下：

如果数值计算的梯度和backpropagation算法计算的梯度是近似相等的话，就说明我们的backpropagation做对了，可以继续用backpropagation去计算梯度，训练模型

注意：在确定了backpropagation做对了之后，应该停止gradient checking，因为这种数值计算梯度的方法是十分的computational expensive，如果不停止的话，模型训练的速度会相当的慢

6、Random initalization

如何设定 $\Theta$ 的初始值？在logistic regression中，初始的参数 $\theta$ 被设定为0，那么如果在neural network中也做这种设定呢？

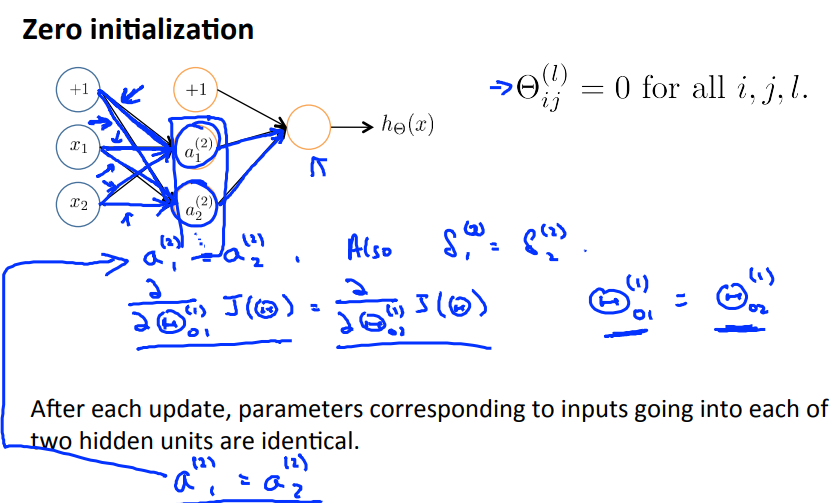
如上所示，如果设定初始的参数全部为0，那么隐藏层的所有的单元的值都会是一样的（在），同时，由后往前传的error $\delta$ 也会是一样的，由此一来，损失函数对同一个输入对应的参数的偏导数也是一样的，也就是说，虽说是同步更新参数，但其实在网络中同一输入出发的的参数永远都是一样的，也就是说计算出来的隐含单元的值也永远是一样的， $a_1^{(2)}$ 永远等于 $a_2^{(2)}$ ，如果有更多的隐含单元的话，也是一样的值。无论隐含层有多少的单元数，它们的值都是相同的，这就是一个极度冗余的现象，而且也根本没有发挥出来多个单元该有的作用。