电子海图开发一百篇第五十五篇-电子江图传输规范 数据模型
1.1向量模型
为进一步简化模型采用了二维平面观察法，为此向量类空间物标可能是零维、一维或二维，分别对应节点、边和面。这三个维数可以表示为物标的属性。
图3中定义了如下关系：
孤立节点……包含在……面
面……包含……离散节点
边……包围……面
面……被包围……边
连接节点……终止……边
边……以为端点……连接节点
边……临接……面
这些关系可用来描述如下四个拓扑级。
－ 无拓扑
－ 链节点
－ 平面图
－ 完全拓扑
这些拓扑级在6.2.2.1.1到6.2.2.1.4节中叙述，给出了各拓扑级的拓扑关系示例图。图中的“点表示”、“线表示”和“面表示”关系是整个数据模型图(图2)中的“被定位”关系的特殊表述。
6.1.1.1.1 无拓扑
无拓扑是一组孤立节点和边，且边不以节点为参数，特征物标决不能是空间物标，点表示被编码成孤立节点，线表示被编码成相连接的一组边，面表示被编码成边的闭合环。若需要逻辑一致性，重合的边必须具有恒等几何性。无拓扑模型在图4中示例。
图3
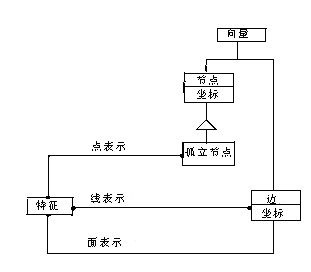
图4
1.2 链节点
一组点和边。其中，每条边必须以一个连接节点作为其始点和终点(可以是同一点)，被参照点的几何性不是边的部分属性(见7.4.7.2节)，可以共用向量物标。点表示被编码成节点(孤立的或连接的)；线表示被编码成边和连接节点序列；面表示被编码成从同一连接节点起始和终止的边的闭合环。禁止线性几何重叠。链节点模型在图5中示例。
1.3 平面图
一组节点和边。其中：在链节点组处，边绝不能相交，只可能与连接节点相临，可以共用向量物标，但有如下限制，即相接的边要共用连接节点，相临的面要共用形成这些面的边界，禁止重叠几何性重复，见图5。
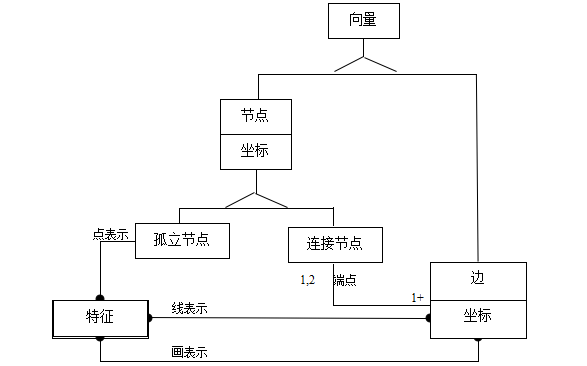
图5
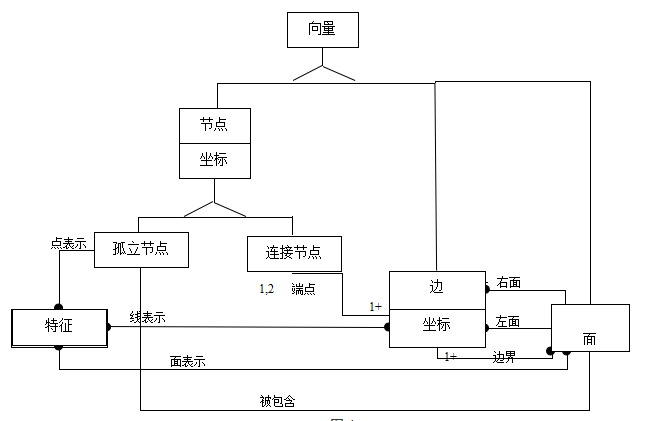
图6
1.4 完全拓扑(见图6) 完全拓扑是指：一组节点、边和面，一个具有特定表面的平面图。整体可以划分为一组
互斥且可穷举的面。孤立节点可以参照包含它的面，而边则必须参照其左和右侧的面。点表示被编码成节点（孤立的或连接的）；线表示被编码成边和连接节点序列；面表示被编码成界面。禁止重叠性几何重复。
