实验一 感知器及其应用
| 这个作业属于哪个课程 | 机器学习实验-计算机18级 |
|---|---|
| 这个作业要求在哪里 | 实验一 感知器及其应用 |
| 学号 | 3180301230 |
一、实验目的
1.理解感知器算法原理,能实现感知器算法;
2.掌握机器学习算法的度量指标;
3.掌握最小二乘法进行参数估计基本原理;
4.针对特定应用场景及数据,能构建感知器模型并进行预测。
二.实验内容
1.安装Pycharm,注册学生版。
2.安装常见的机器学习库,如Scipy、Numpy、Pandas、Matplotlib,sklearn等。
3.编程实现感知器算法。
4.熟悉iris数据集,并能使用感知器算法对该数据集构建模型并应用
三.实验报告要求
-
按实验内容撰写实验过程;
-
报告中涉及到的代码,每一行需要有详细的注释;
-
按自己的理解重新组织,禁止粘贴复制实验内容!
四.实验结果
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris #载入Fisher的鸢尾花数据
#Matplotlib是Python的一个绘图库
import matplotlib.pyplot as plt
%matplotlib inline
# load data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names) #是一个表格
df['label'] = iris.target # 表头字段就是key
df.plot(figsize = (12, 8)) # 利用dataframe做简单的可视化分析

#
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label'] # 选择其中的4个特征进行训练
df.label.value_counts()
2 50
1 50
0 50
Name: label, dtype: int64
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')#绘制散点图
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')#给图加上图例
plt.ylabel('sepal width')
plt.legend()

data = np.array(df.iloc[:100, [0, 1, -1]]) # 取前100条数据,为了方便展示,取2个特征
X, y = data[:,:-1], data[:,-1] # 数据类型转换,为了后面的数学计算
y = np.array([1 if i == 1 else -1 for i in y])
# 数据线性可分,二分类数据
# 此处为一元一次线性方程
class Model:
def __init__(self):
self.w = np.ones(len(data[0])-1, dtype=np.float32)
self.b = 0 #初始w/b的值
self.l_rate = 0.1
# self.data = data
def sign(self, x, w, b):
y = np.dot(x, w) + b #求w,b的值
#Numpy中dot()函数主要功能有两个:向量点积和矩阵乘法。
#格式:x.dot(y) 等价于 np.dot(x,y) ———x是m*n 矩阵 ,y是n*m矩阵,则x.dot(y) 得到m*m矩阵
return y
# 随机梯度下降法
#随机梯度下降法(SGD),随机抽取一个误分类点使其梯度下降。根据损失函数的梯度,对w,b进行更新
def fit(self, X_train, y_train): #将参数拟合 X_train数据集矩阵 y_train特征向量
is_wrong = False
#误分类点的意思就是开始的时候,超平面并没有正确划分,做了错误分类的数据。
while not is_wrong:
wrong_count = 0 #误分为0,就不用循环,得到w,b
for d in range(len(X_train)):
X = X_train[d]
y = y_train[d]
if y * self.sign(X, self.w, self.b) <= 0:
# 如果某个样本出现分类错误,即位于分离超平面的错误侧,则调整参数,使分离超平面开始移动,直至误分类点被正确分类。
self.w = self.w + self.l_rate*np.dot(y, X) #调整w和b
self.b = self.b + self.l_rate*y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
return 'Perceptron Model!'
#线性可分可用随机梯度下降法
def score(self):
pass
# 拟合
perceptron = Model()
perceptron.fit(X, y)
'Perceptron Model!'
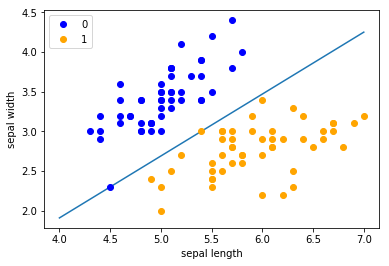
x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
#定义感知机
from sklearn.linear_model import Perceptron
#使用训练数据进行训练
clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False)
#得到训练结果,权重矩阵
clf.fit(X,y)
Perceptron(alpha=0.0001, class_weight=None, eta0=1.0, fit_intercept=False,
max_iter=1000, n_iter=None, n_jobs=1, penalty=None, random_state=0,
shuffle=False, tol=None, verbose=0, warm_start=False)
print(clf.coef_)//输出感知机模型参数
[[ 74.6 -127.2]]
#超平面的截距 Constants in decision function.
print(clf.intercept_)
[0.]
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

五.实验小结
机器学习是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。
最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。


