第七篇博客
| 这个作业属于哪个班级 |
| ---- | ---- | ---- |
| 这个作业的地址 |
| 这个作业的目标 | 学习栈和队列的结构设计及运算操作 |
| 姓名 | 卢伟杰 |
0.PTA得分截图

1.本周学习总结(0-5分)
1.1 栈
-
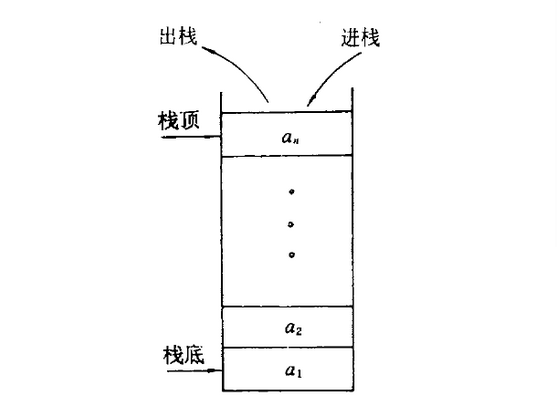
画一个栈的图形,是一种只能在一端进行插入或删除操作的线性表;
允许插入、删除操作的一端称为栈顶,表的另一端称为栈底,也称为后进先出表;
-
顺序栈的结构、操作函数
- 顺序栈的结构
typedef struct
{
ElemType data[MaxSize]; //存放栈中的数据元素
int top; //栈顶指针
}SaStack //顺序栈类型
- 初始化栈
void InitStack(SqStack * &s)
{
s=(SqStack *)malloc(sizeof(SqStack));
s->top = -1;
}
- 销毁栈
void DestroyStack(SqStack * &s)
{
free(s);
}
- 判断栈是否为空
bool StackEmpty(SqStack * s)
{
return(s->top == -1);
}
- 进栈
bool Push(SqStack * &s,ElemType e)
{
if(s->top == MaxSize-1)
return false;
s->top++;
s->data[s->top] = e;
return true;
}
- 出栈
bool Pop(SqStack * &s,ElemType &e)
{
if(s->top == -1)
return false;
e =s->data[s->top]
s->top--;
return true;
}
- 取栈顶元素
bool GetTop(SqStack * s,ElemType &e)
{
if(s->top == -1)
return false;
e =s->data[s->top]
return true;
}
-
顺序栈四个要素:
-
栈空的条件:s->top == -1.
-
栈满的条件:s->top == MaxSize-1.
-
元素e的进栈操作:先将栈顶指针top增1,然后将元素e放在栈顶指针处.
-
出栈操作:先将栈顶指针top处的元素取出放在e中,然后将栈顶指针减1.
-
-
链栈的结构、操作函数
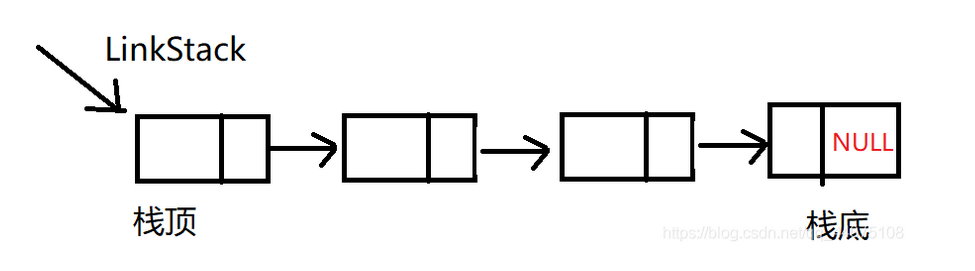
- 链栈的结构
typedf struct linknode
{
ElemType data; //数据域
struct linknode * next; //指针域
}LinkStNode; //链栈节点类型
- 初始化栈
void InitStack(LinkStack *s)
{
*s = NULL;
}
- 销毁栈
void Destroy(LinkStack *s)
{
free(s);
}
- 判断栈是否为空
void Pop(LinkStack *s)
{
StackNode *p = *s;
*s = p->next;
free(p);
p = NULL;
}
- 进栈
void Push(LinkStack *s, ElemType x)
{
StackNode *t = (StackNode*)malloc(sizeof(StackNode));
assert(t != NULL);
t->data = x;
if(*s == NULL)
{
*s = t;
t->next = NULL;
}
else
{
t->next = *s;
*s = t;
}
}
- 出栈
void Pop(LinkStack *s)
{
StackNode *p = *s;
*s = p->next;
free(p);
p = NULL;
}
- 取栈顶元素
bool GetTop(LinkStack *s, ElemType *v)
{
if(IsEmpty(s))
{
printf("栈空间已空,不能取栈顶元素.\n");
return false;
}
*v = (*s)->data;
return true;
}
-
链栈四个要素:
-
栈空的条件:s->next == NULL.
-
栈满的条件:链栈中可以看成不存在栈.
-
元素e的进栈操作:新建节点存放e,将节点插入到头节点之后.
-
出栈操作:取出首节点的data值并将其删除.
-
1.2 栈的应用
-
算术表达式:
-
中缀表达式:运算符位于两个操作数中间的表达式.
-
后缀表达式:运算符在操作数的后面.
-
前缀表达式:运算符在操作数的前面.
-
-
算术表达式转换成后缀表达式:
-
操作数之间的相对次序是不变的,但运算符的相对次序可能不同,同时还要出去括号。
-
在转换时需要从左到右扫描算术表达式。
-
优先级高于栈顶入栈,低于栈顶出栈。
-
1.3 队列
-
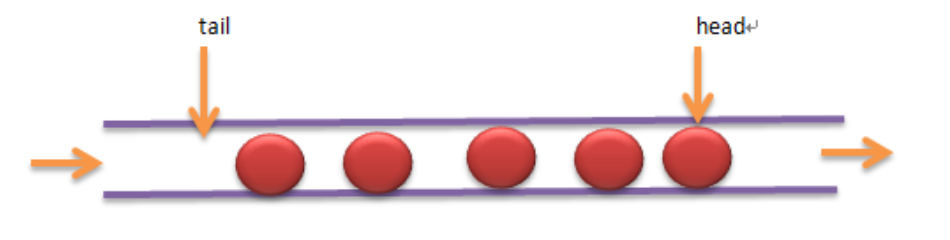
画一个队列的图形,是一种操作受限的线性表允许一端插入、另一端删除。
-
顺序队列的结构、操作函数
- 顺序队列的结构
typedef struct
{
ElemType data[MaxSize] //存放队中元素
int front, rear; //队头和队尾指针
}SqQueue; //顺序队类型
- 初始化队列
void InitQueue(SqQueue * &q)
{
q = (SqQueue *)malloc(sizeof(SqQueue));
q->front = q->rear = -1;
}
- 销毁队列
void DestoryQueue(Squeue * &q)
{
free(q);
}
- 判断队列是否为空
bool QueueEmpty(SqQueue * Q)
{
return(q->front == q->rear);
}
- 进队列
Status EnQueue(SqQueue *Q,QElemtype e)
{
if(Q->rear==QUEUESIZE)
{
return ERROR;
}
Q->base[Q->rear]=e;
Q->rear++;
return OK;
}
- 出队列
Status DeQueue(SqQueue *Q,QElemtype *e)
{
if(Q->front==Q->rear)
{
return ERROR;
}
*e=Q->base[Q->front];
Q->front++;
return OK;
}
-
顺序队列四个要素:
-
队空的条件:q->front == q->rear.
-
队满的条件:q->rear == MaxSize - 1.
-
元素e的进队操作:先将rear增1,然后将元素e放在data数组的rear位置.
-
出队操作:先将front增1,然后取出data数组中front位置的元素.
-
-
环形队列的结构、操作函数
- 环形队列的结构
typedef struct
{
ElemType data[MaxSize] //存放队中元素
int front; //队头指针
int count; //队列中的元素个数
}SqQueue; //顺序队类型
- 初始化队列
void InitQueue(SqQueue * &q)
{
q = (SqQueue *)malloc(sizeof(SqQueue));
q->front = q->rear = 0;
}
- 销毁队列
void DestoryQueue(Squeue * &q)
{
free(q);
}
- 判断队列是否为空
bool QueueEmpty(SqQueue * Q)
{
return(q->front == q->rear);
}
- 进队列
int enQueue(QueueType *&q, ElemType x)
{
int rear;
if (q->count ==Max) //队满溢出
return 0;
else
{
rear=(q->front+q->count)%Max;
rear=(rear+1)%Max;
q->data[rear]=x;
q->count++;
return 1;
}
}
- 出队列
int deQueue(QueueType *&q,ElemType &x)
{
if(q->count==0)
return 0;
else
{
q->front=(q->front+1)%Max;
x=q->data[q->front];
q->count--;
}
}
- 链队列的结构、操作函数
- 链队列的结构
typedef struct qnode
{
ElemType data; //存放队中元素
struct qnode * next; //下一个节点指针
}DataNode; //链队数据节点的类型
- 初始化队列
void InitQueue(LinkQuNode * &q)
{
q = (LinkQuNode *)malloc(sizeof(LinkQuNode));
q->front = q->rear = NULL;
}
- 销毁队列
bool DestoryQueue(LinkQueue &Q)
{
while(Q.front)
{
p=Q.front->next;
delete Q.front;
Q.front=p;
}
return true;
}
- 判断队列是否为空
bool QueueEmpty(LinkQuNode * Q)
{
return(q->rear == NULL);
}
- 进队列
bool EnQueue(LinkQueue &Q,int e)
{
QNode *p=new QNode;
p->data=e;
p->next =NULL;
Q.rear->next=p;
Q.rear=p;
Q.rear=p;
return true;
}
- 出队列
bool DeQueue(LinkList &Q,int &e)
{
if(Q.front==Q.rear)
{
return false;
}
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if(Q.rear==p)
{
Q.rear=Q.front;
}
delete p;
return true;
}
-
链式队列四个要素:
-
队空的条件:rear == NULL.
-
队满的条件:不考虑.
-
元素e的进队操作:新建节点存放e,将节点插入尾节点,让rear指向新的尾节点.
-
出队操作:取队头节点的data值并将其删除.
-
2.PTA实验作业(4分)
2.1 符号配对
2.1.1 解题思路及伪代码
- 定义字符型数组s 输入s
- for循环i=0 to i<len
- 不是符号 跳过以下语句
- 为左符号 进栈
- 为右符号
- 栈空 退出程序(因为右符号没有左符号和它配对 表达式已经配对错误了)
- 为右符号且配对 出栈
- 结束for循环
- 接下来判断是否配对成功
- 栈空且i=len 配对成功
- i不等于len 配对失败,输出no以及栈顶(栈为空不输出)
2.1.2 总结解题所用的知识点
-
需要用到数组并进行遍历进行判断;
-
栈的后进先出的应用;
-
栈基本操作数的使用,如判断栈空、进栈、出栈等;
#include<iostream>
#include<stdio.h>
#include<stack>
#include<string.h>
using namespace std;
stack <char> q;
int main()
{
char s[100];
scanf("%s",s);
int len=strlen(s);
int i;
for(i=0;i<len;i++)
{
if(s[i]!='{'&&s[i]!='['&&s[i]!='('&&s[i]!='}'&&s[i]!=']'&&s[i]!=')')
{
continue;
}
if(s[i]=='{'||s[i]=='['||s[i]=='(')
q.push(s[i]);
else if(s[i]==']'||s[i]=='}'||s[i]==')')
{
if(q.empty())
{
break;
}
else
{
if((s[i]==']'&&q.top()=='[')||(s[i]==')'&&q.top()=='(')||(s[i]=='}'&&q.top()=='{'))
{
q.pop();
}
}
}
}
if(q.empty()&&i==len)
cout<<"yes";
else if(q.empty())
cout<<"no";
else
{
cout<<q.top()<<"\n";
cout<<"no";
}
}
2.2 报数游戏
2.2.1 解题思路及伪代码
- 定义m,N,数组line
- 定义队列qu;
- m<N
- 数组line中的N个元素全部进队
- 队列qu不为空
- 报数m次,不为m的报数后重新入队,报数为m的直接出队 ,输出
- m>=N 输出输入错误
2.2.2 总结解题所用的知识点
-
队列的基本操作函数的应用;
-
数组的建立以及遍历;
-
主要就是队列的不断出队和重新入队,利用队列先进先出的特点;
#include <iostream>
#include<set>
using namespace std;
int main()
{
set<int> s;
int m, n;
cin >> n >> m;
if (m >= n) {
cout << "error!";
return 0;
}
for (int i = 0; i < n; i++) {
s.insert(i+1);
}
set<int>::iterator it;
it = s.begin();
int flag = 0;
while (s.size() != 0) {
for (int i = 1; i < m; i++) {
if (!(it != s.end())) {
it = s.begin();
}
it++;
}
if (!(it != s.end())) {
it = s.begin();
}
if (flag == 0) {
cout << *it;
flag = 1;
}
else {
cout <<" "<< *it;
}
int c = *it;
s.erase(c);
int j = 1;
while (1) {
it = s.find((c + j) % n);
if (it != s.end())
break;
else
j++;
if (j == n) {
break;
it = s.end();
}
}
if (!(it != s.end())) {
it = s.begin();
}
}
}
3.阅读代码(0--1分)
3.1 题目及解题代码
题目描述
小易老师是非常严厉的,它会要求所有学生在进入教室前都排成一列,并且他要求学生按照身高不递减的顺序排列。有一次,n个学生在列队的时候,小易老师正好去卫生间了。学生们终于有机会反击了,于是学生们决定来一次疯狂的队列,他们定义一个队列的疯狂值为每对相邻排列学生身高差的绝对值总和。由于按照身高顺序排列的队列的疯狂值是最小的,他们当然决定按照疯狂值最大的顺序来进行列队。现在给出n个学生的身高,请计算出这些学生列队的最大可能的疯狂值。小易老师回来一定会气得半死。
输入描述:
输入包括两行,第一行一个整数n(1 ≤ n ≤ 50),表示学生的人数
第二行为n个整数h[i](1 ≤ h[i] ≤ 1000),表示每个学生的身高
输出描述:
输出一个整数,表示n个学生列队可以获得的最大的疯狂值。
如样例所示:
当队列排列顺序是: 25-10-40-5-25, 身高差绝对值的总和为15+30+35+20=100。
这是最大的疯狂值了。
示例1
输入
5
5 10 25 40 25
输出
100
n = int(input())
heights = [each_height for each_height in map(int, input().split())]
s2l = sorted(heights) # 从小到大排
l2s = s2l[::-1] # 从大到小排
results = []
pop_small = True
left = True
for i in range(n):
if i == 0:
results.append(s2l.pop()) # 把最大的元素放进来
elif i == n - 1:
if pop_small:
temp = l2s.pop()
if abs(results[0] - temp) > abs(results[n - 2] - temp):
results.insert(0, temp)
else:
results.append(temp)
else:
temp = s2l.pop()
if abs(results[0] - temp) > abs(results[n - 2] - temp):
results.insert(0, temp)
else:
results.append(temp)
elif pop_small:
if left:
results.insert(0, l2s.pop())
left = False
else:
results.append(l2s.pop())
left = True
pop_small = False
else:
if left:
results.insert(0, s2l.pop())
left = False
else:
results.append(s2l.pop())
left = True
pop_small = True
print(sum([abs(results[i] - results[i + 1]) for i in range(n - 1)]))
3.2 该题的设计思路
- 把原序列排序,先取出最大的数放在results中,然后在最大数的两边放两个最小的数,接着在两个最小的数两边放第二、第三大的数
依次类推,再放入最后一个数的时候要注意,计算它放在最左侧或最右侧时与相邻的元素差值的绝对值,选择把它放在绝对值大的那一侧




