时间序列分析1.基本数学概念

1.均值、方差、协方差、相关系数

1.1 期望

1.1.1 期望的定义

令\(X\)具有概率密度函数\(f(x)\),并且令\((X,Y)\)对具有联合概率密度函数\(f(x,y)\)。
定义\(X\)的期望值为：\(E(X)={\int\limits_{-\infty}^\infty}xf(x)dx\)。

1.1.2 期望的性质

1. \(E(aX+bY+c) = aE(X)+bE(Y)+c\)
2. 当\(X\)和\(Y\)相互独立时，\(E(XY)=E(X)E(Y)\)

1.2 方差

1.2.1 方差的定义

随机变量\(X\)的方差定义为：\(D(X)=E\{[X-E(X)]^2\}\)，方差通常还记为\(Var(X)\)、\(\mu^2\)。
若\(X\)是离散型随机变量，则\(D(X)=\sum_{k=1}^{\infty}[x_k-E(x)]^2p_k\).
若\(X\)是连续型随机变量，则\(D(X)=\int_{-\infty}^{\infty}[x-E(x)]^2f(x)dx\)

\(D(X)=E\{[X-E(X)]^2\)
\(=E\{X^2-2XE(X)+[E(X)]^2\}\)
\(=E(X^2)-2E(X)E(X)+[E(x)]^2\)
\(=E(X^2)-[E(X)]^2\)

1.2.2 方差的性质

1. \(D(aX+b)=a^2D(X)\)
2. 若\(X\)与\(Y\)相互独立，则\(D(X\pm Y) = D(X)+D(Y)\)
3. 若\(X\)与\(Y\)不独立，则\(D(X\pm Y)=D(X)+D(Y)\pm2Cov(X,Y)\)

1.3 协方差

1.3.1 协方差的定义

\(Cov(X,Y)=E\{(X-E(X))(Y-E(Y))\}=E(XY)-E(X)E(Y)\)

1.3.2 协方差的性质

1. \(Cov(a+bX,c+dY)=bdCov(X,Y)\)
2. \(Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)\)
3. \(Cov(X,X)=D(X)\)
4. \(Cov(X,Y)=Cov(Y,X)\)
5. 若\(X\)与\(Y\)相互独立，那么\(Cov(X,Y)=0\)

1.4 相关系数

1.4.1 相关系数的定义

\(X\)与\(Y\)的相关系数用\(Corr(X,Y)\)或者\(\rho\)表示，定义如下：

\[\rho=Corr(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y))}} \]

1.4.2 相关系数的性质

1. \(-1\leq Corr(X,Y)\leq 1\)
2. \(Corr(X,Y)=\pm 1\)的充要条件是，存在常数\(a\)和\(b\)，使得\(Pr(Y=aX+b)=1\).
3. 相关系数如果为正号，则表示正相关，如果为负号，则表示负相关。通俗点说，正相关就是变量会与参照数同方向变动，负相关就是变量与参照数反向变动；
4. 取值为0，这是极端，表示不相关。取值接近\(\pm 1\)时说明线性相关程度强。

1.5 时间序列与随机过程

对于随机变量序列\(\{Y_t: t=0,1,2,3,...\}\)称为一个随机过程，并以之作为观测时间序列的模型。

1.5.1 自协方差函数

\[\gamma_{t,s}=Cov(Y_t,Y_s),t,s=0,1,2,3,... \]

其中\(Cov(Y_t,Y_s)=E[(Y_t-\mu_t)(Y_s-\mu_s)]\)。

1.5.2 自相关函数

\({{\rho}_{t,s}}={Cov(Y_t,Y_s)},t,s=0,1,2,3,...\)
其中：

\[{Corr(Y_t,Y_s)} =\frac{Cov(Y_t,Y_s)}{\sqrt{Var(Y_t)Var(Y_s)}} =\frac{\gamma _{t,s}}{\sqrt{\gamma _{t,t}\gamma _{s,s}}}\]

1.5.3 重要结论

在研究不同时间序列的模型协方差的性质时，反复用到如下结论：如果\(c_1,c_2,c_3,...c_m\)和\(d_1,d_2,d_3,...d_n\)表示常数，\(t_1,t_2,t_3,...t_m\)和\(s_1,s_2,s_3,...s_n\)表示时间点，则有：

\[{Cov[\sum_{i=1}^{m}{c_iY_{t_i}},\sum_{j=1}^{n}{d_iY_{s_j}}]} =\sum_{i=1}^{m}\sum_{j=1}^{n}c_id_jCov(Y_{t_i},Y_{s_j})\]

2.平稳性

平稳性的基本思想是，决定过程特性的统计规律不随着时间的变化而变化。

2.1 严平稳

如果对于一切时间间隔\(k\)和时间点\(t_1,t_2,t_3,...,t_n\)，都有\(Y_{t_1},Y_{t_2},...,Y_{t_n}\)与\(Y_{t_1-k},Y_{t_2-k},...,Y_{t_n-k}\)的联合分布相同，则称过程\(\{Y_t\}\)为严平稳。

2.2 弱平稳

2.2.1 弱平稳时间序列的条件

1.\(E(Y_t)=\mu\)，序列的均值应该是一个常数，而不是随时间变化的函数。下图中左图满足要求，而右图的均值是随时间而变化的。

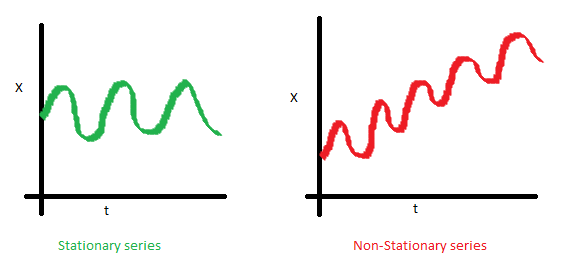
2.\(Var(Y_t)=\gamma\)，序列的方差为一个常数，而不随时间的变化。

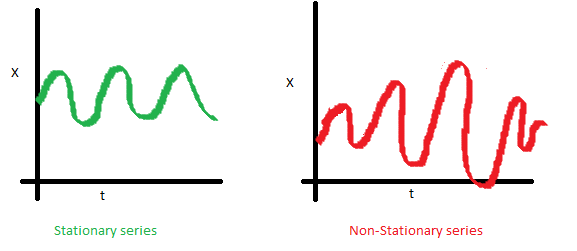
3.\(Cov(Y_t,Y_{t+k})=\gamma_{0,k}\),序列协方差的值只与时间间隔\(k\)有关，与时间\(t\)无关。

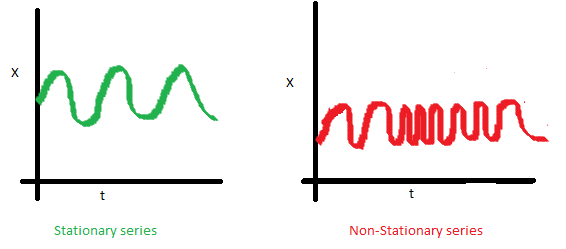
以上的三个条件必须全部满足，才能被称为弱平稳的时间序列。我们建立时间序列模型时必须要求时间序列是平稳的，这是因为我们用时间序列做预测时，我们的随机变量的基本特性必须能在包括未来阶段的一个长时期里维持不变，否则，基于历史和现状来预测未来的思路便是错误的。所以在时间序列建模时第一步就是要将不平稳的序列平稳化，可以采用差分等方法。

2.2.2 弱平稳时间序列的自相关系数

弱平稳序列的自相关系数：

\[\rho_k = \frac{Cov(x_t,x_{t,k})}{\sqrt{Var(x_t)Var(x_{t-k})}} =\frac{Cov(x_t,x_{t-k})}{Var(x_t)} =\frac{\gamma_k}{\gamma_0}\]

2.3 随机游动

令\(e_1,e_2,e_3,...\)为均值为\(0\)，方差是\({\sigma_e^2}\)的独立同分布的随机变量序列，观测时间序列\({Y_t:t=1,2,3,...}\)构造如下：
\(Y_1=e_1\)
\(Y_2=e_1+e_2\)
\(...\)
\(Y_t=e_1+e_2+e_3\)
也可以写成：

\[Y_t=Y_{t-1}+e_t \]

其初始条件为\(Y_1=e_1\)，\(e\)指沿数轴（前向或后向）方向游动的步长大小，\(Y_t\)是在时刻\(t\)，“漫步者”到达的位置。
对于所有的\(t\):
均值：\(\mu_t=0\)
方差：\(D(Y_t)=t\sigma_e^2\)
自协方差：\(\gamma_{t,s}=t\sigma_e^2\)
自相关系数：\(\rho_{t,s}=\frac{\gamma_{t,s}}{\sqrt{\gamma_{t,t}\gamma_{s,s}}}=\sqrt{\frac{t}{s}},1\leq t\leq s\)

可以看到，随机游动的方差、自协方差均是随时间线性增长的，所以随机游动不是平稳序列。

2.4 白噪声

如果序列\(\{Y_t\}\)的所有观测值都是独立同分布的，而且他的均值\(\mu\)和方差\(\sigma^2\)都是有穷的常数，则该序列称为白噪声(white noise)或纯随机过程(purely random process)。
白噪声的三个条件：

1. 有限均值
2. 有限方差
3. 独立同分布
   如果白噪声的分布是均值为0的正态分布，则\(\{Y_t\}\)也称为高斯白噪声。
   \(Pr(e_{t_1}\leq x_1,e_{t_2}\leq x_2,...,e_{t_n}\leq x_n)\)
   \(=Pr(e_{t_1}\leq x_1)Pr(e_{t_2}\leq x_2)...Pr(e_{t_n}\leq x_n)(根据独立性)\)
   \(=Pr(e_{t_1-k}\leq x_1)Pr(e_{t_2-k}\leq x_2)...Pr(e_{t_n-k}\leq x_n)(同分布)\)
   \(=Pr(e_{t_1-k}\leq x_1,e_{t_2-k}\leq x_2,...,e_{t_n-k}\leq x_n) (根据独立性)\)
   根据定义要求，显然白噪声是严平稳的。

---

参考资料

<Time Series Analysis with Applications in R>