六面体网格 质量评估

简介

六面体网格生成过程中往往要查看网格的质量，通常采用计算最小雅克比值和平均雅克比值。

算法流程

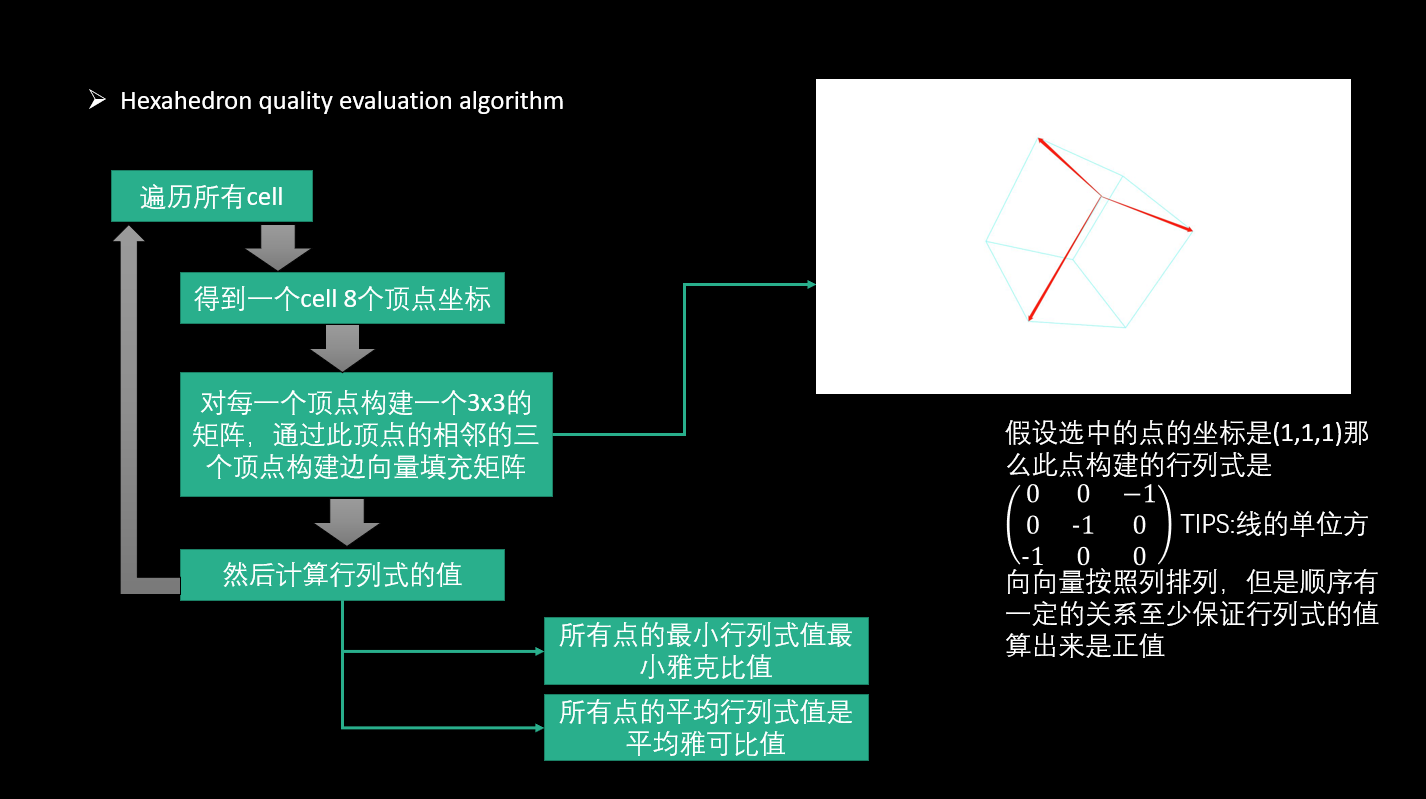
参考链接

http://staff.ustc.edu.cn/~fuxm/code/Volume_Framework.zip

发现问题

就是生成网格文件在 hexalab.net 有些网格节点显示不出来。

解决问题

脑子中猜想各种问题的解决方案，顶点顺序？

真实解决

生成一个cube文件就是最简单的立方体，然后自己写了关于网格质量的代码，scaledJacobian的生成。然后和官网显示的一样。
然后查看了官网的代码，重写了生成Jacobian的矩阵。

官网相关代码

inline
void hex_edges(const Vector3f & p0, const Vector3f & p1, const Vector3f & p2, const Vector3f & p3,
               const Vector3f & p4, const Vector3f & p5, const Vector3f & p6, const Vector3f & p7,
               Vector3f L[], const bool normalized)
{
    L[0] = p1 - p0;    L[4] = p4 - p0;    L[8]  = p5 - p4;
    L[1] = p2 - p1;    L[5] = p5 - p1;    L[9]  = p6 - p5;
    L[2] = p3 - p2;    L[6] = p6 - p2;    L[10] = p7 - p6;
    L[3] = p3 - p0;    L[7] = p7 - p3;    L[11] = p7 - p4;

    if(normalized) for(int i=0; i<12; ++i) L[i].normalize();
}

inline
void hex_principal_axes(const Vector3f & p0, const Vector3f & p1, const Vector3f & p2, const Vector3f & p3,
                        const Vector3f & p4, const Vector3f & p5, const Vector3f & p6, const Vector3f & p7,
                        Vector3f X[], const bool normalized)
{
    X[0] = (p1 - p0) + (p2 - p3) + (p5 - p4) + (p6 - p7);
    X[1] = (p3 - p0) + (p2 - p1) + (p7 - p4) + (p6 - p5);
    X[2] = (p4 - p0) + (p5 - p1) + (p6 - p2) + (p7 - p3);

    if(normalized) for(int i=0; i<3; ++i) X[i].normalize();
}

inline
void hex_subtets(const Vector3f L[], const Vector3f X[], const int id, Vector3f tet[])
{
    switch(id)
    {
        case 0: tet[0]= L[0];  tet[1]= L[3];  tet[2]= L[4]; break; // 1, 3, 4
        case 1: tet[0]= L[1];  tet[1]=-L[0];  tet[2]= L[5]; break; // 2, 0, 5
        case 2: tet[0]= L[2];  tet[1]=-L[1];  tet[2]= L[6]; break; // 3, 1, 6
        case 3: tet[0]=-L[3];  tet[1]=-L[2];  tet[2]= L[7]; break; // 0, 2, 7
        case 4: tet[0]= L[11]; tet[1]= L[8];  tet[2]=-L[4]; break;
        case 5: tet[0]=-L[8];  tet[1]= L[9];  tet[2]=-L[5]; break;
        case 6: tet[0]=-L[9];  tet[1]= L[10]; tet[2]=-L[6]; break;
        case 7: tet[0]=-L[10]; tet[1]=-L[11]; tet[2]=-L[7]; break;
        case 8: tet[0]= X[0];  tet[1]= X[1];  tet[2]= X[2]; break;
    }
}

HL_QUALITY_MEASURE_DEF(scaled_jacobian)
{
    Vector3f L[12];
    Vector3f X[3];
    hex_edges(p0, p1, p2, p3, p4, p5, p6, p7, L, true);
    hex_principal_axes(p0, p1, p2, p3, p4, p5, p6, p7, X, true);

    float sj[9];
    for(int i=0; i<9; ++i)
    {
        Vector3f tet[3];
        hex_subtets(L, X, i, tet);
        sj[i] = determinant(tet[0], tet[1], tet[2]);
    }
    float msj = *std::min_element(sj, sj+9);
    if(msj > 1.0001) return -1.0;
    return msj;}

TIPS

其中for(int i=0; i<9; ++i) i 可以只遍历到8 我觉得没必要遍历到9.
如果遇到所有的生成的 scaledJacobian 最小的值还小于0， 我就交换了顶点序列，就是将前四个和后四个顶点顺序进行了交换。
大约花了我2天时间，发现其实并不难另外再送大家两个文档，送佛送到家

核心文档名字 自己去sci_hub下载嘿嘿

一个文档是 verdict_quality_library 对于所有的网格的质量判决，包括三角网格，四边形网格，和六面体网格等等。
另一个文档是 ACHIEVING FINITE ELEMENT MESH QUALITY VIA OPTIMIZATION OF THE JACOBIAN MATRIX NORM AND ASSOCIATED QUANTITIES 其实就是上一个文档的真实使用的论文。说实话代码更香~~