Aizu - ALDS1_5_C 递归+几何推导
Koch Curve
Write a program which reads an integer n and draws a Koch curve based on recursive calles of depth n.
The Koch curve is well known as a kind of fractals.
You can draw a Koch curve in the following algorithm:
- Divide a given segment (p1, p2) into three equal segments.
- Replace the middle segment by the two sides of an equilateral triangle (s, u, t) of the same length as the segment.
- Repeat this procedure recursively for new segments (p1, s), (s, u), (u, t), (t, p2).
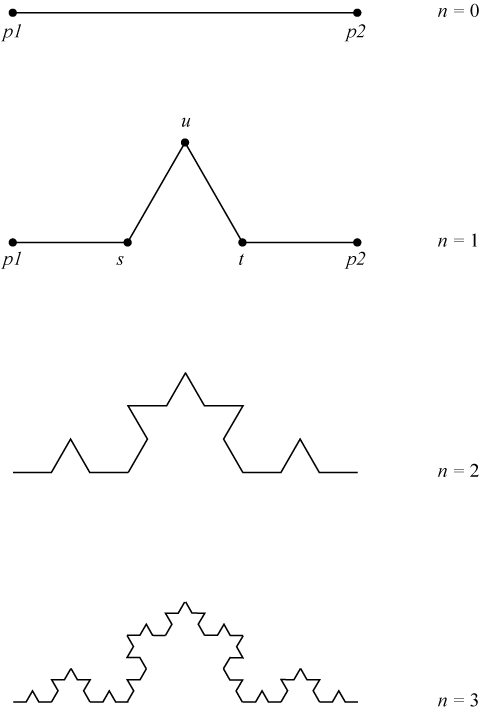
You should start (0, 0), (100, 0) as the first segment.
Input
An integer n is given.
Output
Print each point (x, y) of the Koch curve. Print a point in a line. You should start the point(0, 0), which is the endpoint of the first segment and end with the point (100, 0), the other endpoint so that you can draw the Koch curve as an unbroken line. Each solution should be given as a decimal with an arbitrary number of fractional digits, and with an absolute error of at most 10-4.
Constraints
- 0 ≤ n ≤ 6
Sample Input 1
1
Sample Output 1
0.00000000 0.00000000 33.33333333 0.00000000 50.00000000 28.86751346 66.66666667 0.00000000 100.00000000 0.00000000
Sample Input 2
2
Sample Output 2
0.00000000 0.00000000 11.11111111 0.00000000 16.66666667 9.62250449 22.22222222 0.00000000 33.33333333 0.00000000 38.88888889 9.62250449 33.33333333 19.24500897 44.44444444 19.24500897 50.00000000 28.86751346 55.55555556 19.24500897 66.66666667 19.24500897 61.11111111 9.62250449 66.66666667 0.00000000 77.77777778 0.00000000 83.33333333 9.62250449 88.88888889 0.00000000 100.00000000 0.00000000
思路:递归控制输出,点坐标几何推导,关于旋转矩阵相关内容参看博客:https://www.cnblogs.com/zhoug2020/p/7842808.html,写的很详细。
电子板写的,手感很差,凑合看吧,这个过程是得出是s,u,t三点坐标的;
Code

1 //Aizu - ALDS1_5_C 2 #include <bits/stdc++.h> 3 4 using namespace std; 5 6 const double pi = acos(-1); 7 8 void koch(int n, pair<double, double> p1, pair<double, double> p2) 9 { 10 if (n == 0) return; 11 12 double th = pi * 60.0 / 180.0; 13 pair<double, double> s, u, t; 14 15 s.first = (2.0 * p1.first + p2.first) / 3.0; 16 s.second = (2.0 * p1.second + p2.second) / 3.0; 17 18 t.first = (p1.first + 2.0 * p2.first) / 3.0; 19 t.second = (p1.second + 2.0 * p2.second) / 3.0; 20 21 u.first = cos(th) * (t.first - s.first) - sin(th) * (t.second - s.second) + s.first; 22 u.second = sin(th) * (t.first - s.first) + cos(th) * (t.second - s.second) + s.second; 23 24 koch(n - 1, p1, s); 25 printf("%.8lf %.8lf\n", s.first, s.second); 26 koch(n - 1, s, u); 27 printf("%.8lf %.8lf\n", u.first, u.second); 28 koch(n - 1, u, t); 29 printf("%.8lf %.8lf\n", t.first, t.second); 30 koch(n - 1, t, p2); 31 } 32 33 int main() 34 { 35 int n; 36 cin >> n; 37 printf("%.8lf %.8lf\n", 0.0, 0.0); 38 koch(n, make_pair(0.0, 0.0), make_pair(100.0, 0.0)); 39 printf("%.8lf %.8lf\n", 100.0, 0.0); 40 return 0; 41 }


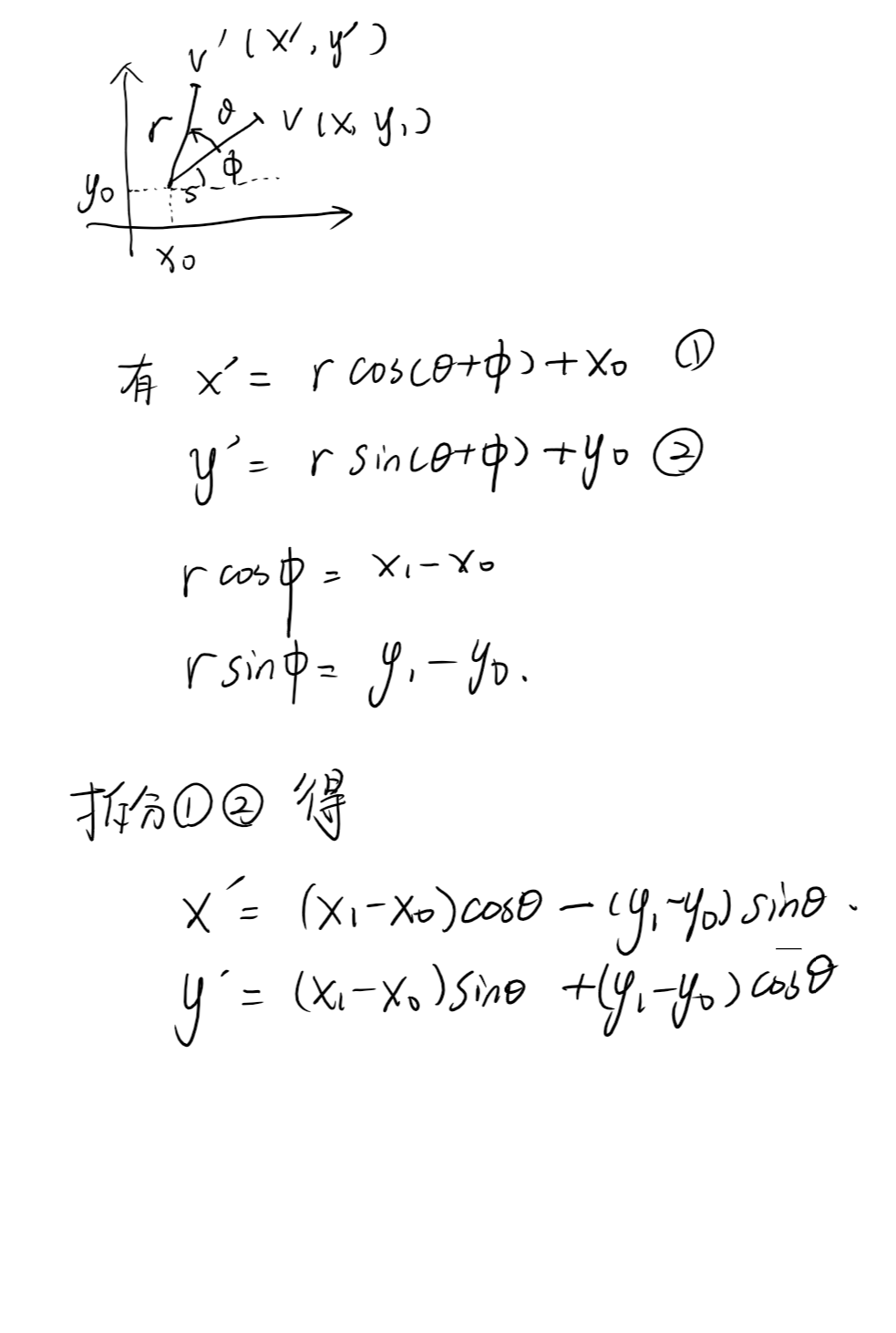


 浙公网安备 33010602011771号
浙公网安备 33010602011771号