概率论基础知识

随机试验：

　　在同一组条件下，对某事物或现象所进行的观察或实验叫随机试验，把观察或实验的结果叫随机事件。如果随机试验的每种结果可以

　　用一个数字作为其代表，则我们称此变量为随机变量，随机变量都具有这种性质和特点：事先可以肯定取值的范围，但不能肯定具体

　　取值是多少。概率论所要研究的是随机变量所取之值的规律，即出现各种结果的可能性如何。随机变量类型包括离散型随机变量和连

      续型随机变量。

概率密度函数：

　　随着连续型数据的不断增加，频率趋于稳定，频率的稳定值就是概率。如果要求整个曲线下方的面积恰好为1，则这条曲线就称为概

　　率密度曲线（PDF).

　　1>.概率密度函数曲线与横轴所围成的面积永远为1

　　2>.随机变量落入一个范围内的概率等于密度函数曲线在这个范围上的积分

离散型随机变量的均值：

　　

连续型随机变量的期望值：

　　

随机变量的方差：

 

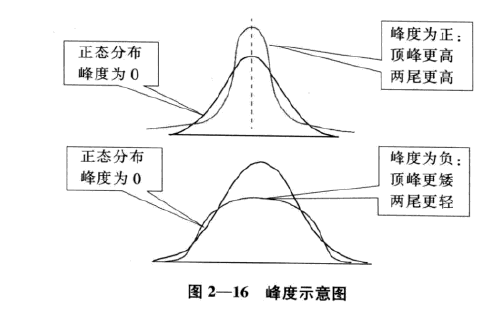
随机变量的偏度与峰度：

　　

　　　　　　　　

　　

 　　　　　　

随机变量的累积分布函数及分位数概念：

　　

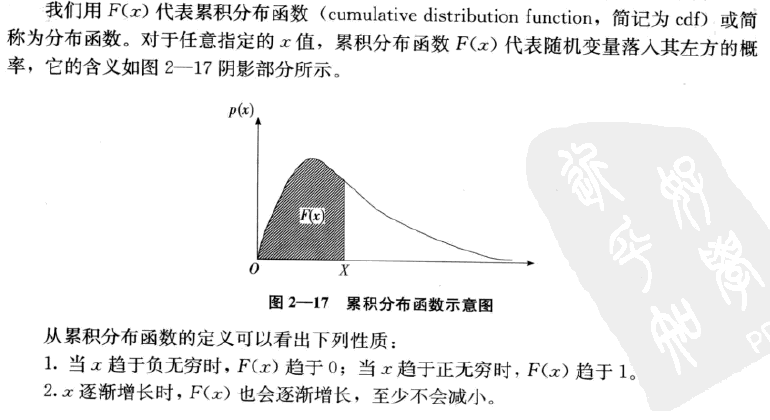
随机变量的分位数：

　　

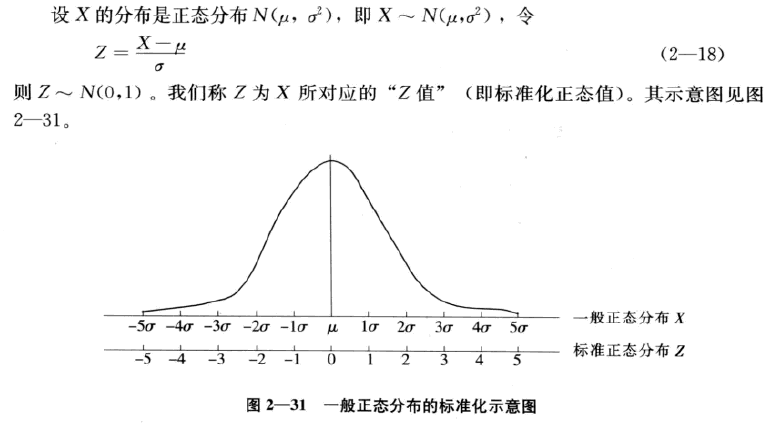
正态分布：

　　

　　

　　　　

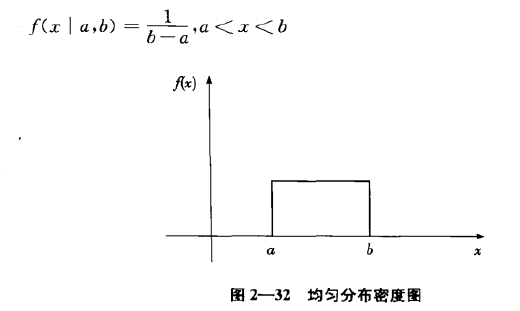
均匀分布：

　　如果连续型随机变量X落入区间(a,b)间的概率为常数，也就是说X落入此区间任一点的概率都相等，则称X在区间(a,b)上服从均匀分布，其密度图形如下：

　　　　　　

　　　　　　　　　　

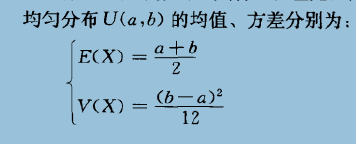
指数分布：

　　

　　

对数正态分布

　　如果随机变量X只取正数值，而取自然对数后，lnX服从正态分布，则称X服从对数正态分布。

　　

二项分布：

　　

　　

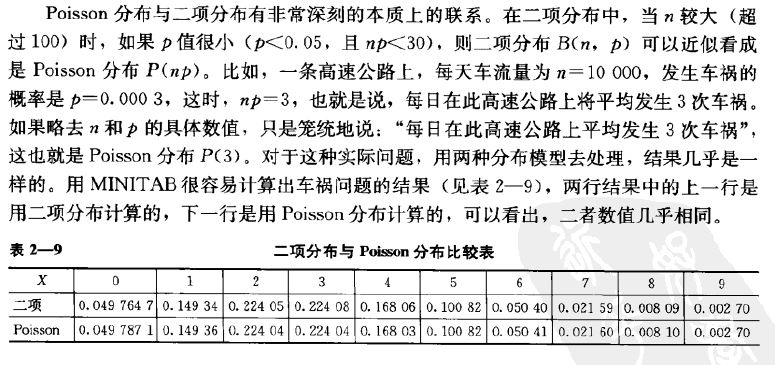
Poisson分布：

　　

　　

中心极限定量：

　　样本平均值的标准差性质

　　

　　样本平均值的分布性质：正态分布