CF1909G Pumping Lemma 题解
题目要求我们对合法三元组进行计数，直接做是困难的，因此考虑通过枚举确定一部分元素再进行判定求解，那我们固定什么呢？固定 \(x\) 和 \(y+z\) 的分界线没啥用，因此我们枚举确定 \(S\) 中 \(x+y\) 和 \(z\) 的分界线，这样能确定一长串 \(y^{k-1}\) 所在的区间。
接着我们不难想到一个 \(O(n^2)\) 的做法，每次找到这次被钦定为 \(y^{k-1}\) 所在的区间的最小周期，枚举这个区间的每个周期作为 \(y\)，然后判一下这个方案行不行，具体来说，我们有两个要求：
-
\(y^{k-1}\) 串前后必须包括在两个字符串的 \(\text{lcp}\) 和 \(\text{lcs}\) 内。
-
\(\text{lcp}(S,T)>|z+y|\)（也即 \(x+y\) 部分必须要包括一个 \(y\)，不难发现这两个条件是等价的）.
利用手段优化这个做法不太容易，因为 \(z\) 和 \(x+y\) 改变的时候整个周期会跟着一起变，而我们又没有快速求区间 Border 的算法，但周期的变化真的那么彻底吗？如下图：
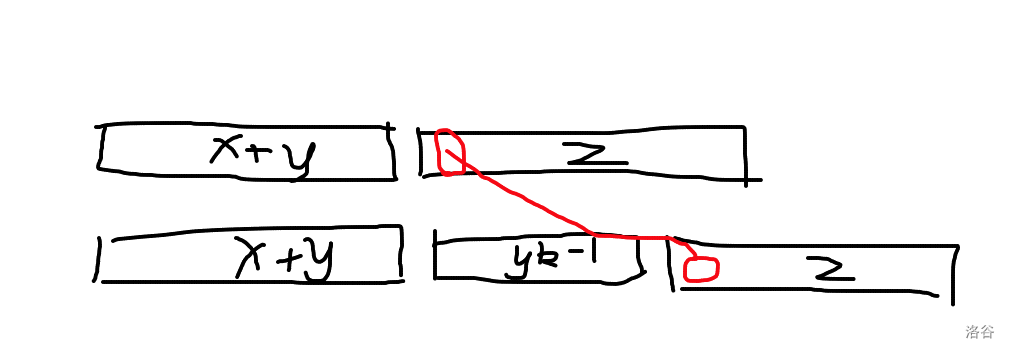
你发现当我们将分割 \(x+y\) 和 \(z\) 的分界线右移时，如果这两个字符串的 \(\text{lcp} > |x+y|\)，也即上面 \(z\) 串第一个字符和 \(y^{k-1}\) 串第一个字符相同（其实这必然满足，不然你的移动是不合法的），然后又有红色部分相同，因此右移边界不过是把 \(y^{k-1}\) 作了循环移位，而循环移位不会改变周期。
因此，就有所有满足上面条件一的 \(y^{k-1}\) 区间周期都相同，而这些区间的左端点取值范围是 \([m-\text{lcs}-(m-n)+1,\text{lcp}+1]\)，这个由条件一可以很方便地得到。
最后，我们还剩一个条件二没有处理，但是你发现假设我们枚举了一个周期，只要把区间左端点取值范围改成 \([m-\text{lcs}-(m-n)+1+|y|,\text{lcp}+1]\) 就可以了，这个条件的充分性显然，而必要性只要考虑如果扩展 \(\text{lcp}\) 就会不满足条件。
总结一下我们要怎么求：直接求出任意一个合法 \(y^{k-1}\) 的最小周期，然后枚举所有周期加上对应合法左端点取值区间的长度即可。
#include<bits/stdc++.h>
#define ll long long
#define N 10000007
using namespace std;
ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0' || ch>'9')f=(ch=='-'?-1:f),ch=getchar();
while(ch>='0' && ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x*f;
}
void write(ll x){
if(x<0)x=-x,putchar('-');
if(x/10)write(x/10);
putchar(x%10+'0');
}
char s[N],t[N];
ll nex[N];
ll get_nex(ll l,ll r){
for(ll i=l+1,j=0;i<=r;i++){
while(j && t[j+l]!=t[i])j=nex[j];
if(t[j+l]==t[i])j++;
nex[i-l+1]=j;
}
return nex[r-l+1];
}
int main(){
#ifdef EAST_CLOUD
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
#endif
ll n=read(),m=read();
scanf("%s",s+1);scanf("%s",t+1);
ll lcp=0,lcs=0;
while(lcp!=n && s[lcp+1]==t[lcp+1])lcp++;
while(lcs!=n && s[n-lcs]==t[m-lcs])lcs++;
ll border=get_nex(lcp+1,lcp+m-n),len=m-n,per=len-border;
if(len%per!=0)per=len;
ll l=m-lcs-len+1,r=lcp+1,ans=0;
for(ll i=per;i<=min(len,r-l+1);i+=per){
if(len%i==0)ans+=(r-l+1)-i;
}
write(ans);
}
