字符串小记 II：字符串自动机

OI 中的自动机指的是“有限状态自动机”，它是对一串信号进行处理的数学模型，一般由以下三部分构成：

1. 字符集（\(\Sigma\)），能够输入进自动机的字符集合。
2. 状态集合（\(Q\)) ，相当于有向图中的节点。
3. 转移函数（\(\delta\)），相当于有向图中的边。

我们通过输入的信息在这个有向图中转移，而这个有向图中的每个节点也拥有着一些信息，比如在 trie 中，我们输入字符并在这个自动机中持续往下走，即在这个自动机上转移，trie 中的每个节点代表一个由根节点到它的路径组成的一个字符串，我们知道现在在哪个节点就能知道当前状态所对应的字符串，注意这个信息是隐式的，我们并不需要实际储存，节点已经代表了信息。

为什么我们需要自动机呢，在一些字符串匹配问题中，暴力地匹配等价于在自动机上转移，那我们何不利用自动机的一些良好性质压缩转移路径。又由于自动机中节点代表的信息是被压缩过的，我们也可以以此优化算法中的冗余状态，这点常见于自动机优化 dp 的题目之中。

本文将简单地说明一下 OI 中常见的各类字符串自动机，重点描述实现的一些注意事项，状态性质与实际的一些用法，由于 trie 的结构较为简单因此本文不会涉及。

1.KMP 自动机

2.子序列自动机

3.AC 自动机（ACAM）

4.回文树 / 回文自动机（PAM）

简单性质

我们建立两个根节点，分别为奇根和偶根，将字符串中所有本质不同子串建立节点，回文串长度为 1 的连到奇根下面，长度为 2 的连到偶根下面，对于其他节点，字符串 \([i,j]\) 代表的节点连到字符串 \([i+1,j-1]\) 代表的节点下方，这形成了一个森林结构，叫做回文树。

若不关注节点所储存的信息和编号，对于每个回文串的一半，我们将其类似地以 trie 的形式插入到奇根和偶根之下，则所得到的森林与这个字符串的回文树是同构的，所以回文树也可以看做每个“半回文串”形成的 trie，我们可以依次类似地构造每个节点的失配指针，指向的节点为当前字符串的最长回文后缀，这样形成的自动机结构叫做该字符串的回文自动机。

具体构造

如何构造出一棵回文自动机呢？具体算法流程如下：

1. 初始化：新建两个编号为 0，1 的节点表示偶根与奇根，之所以选择这两个编号的节点是为了防止越界，接着将 0 节点长度设为 0，1节点长度设为 -1，这是为了后面节点长度合理与跳失误指针时不会死循环，因为单个字符也算回文串。

2. 插入字符：当插入一个新字符时，我们不断跳插入上一个字符时所获得的节点（记为 \(last\) 的失配指针（因为上一个节点代表的字符串为插入这个字符前总字符串的最长回文后缀），直到某个状态再往前一个字符与新插入的字符相同，记跳到的状态为 \(p\) 。

   这代表我们找到了插入当前字符后总字符串的最长回文后缀。判断是否存在代表着这个回文后缀的节点，即看当前节点有没有一个当前字符类型的转移，不存在进入 3，否则进入 4。

3. 若是不存在对应节点，那我们新建一个节点 \(q\) ，然后跳 \(fail_p\) 的失配指针直到某个状态再往前一个字符与新插入的字符相同，这个状态即为 \(fail_q\) ，接着 \(len_p+2 \rightarrow len_q\) ，\(q \rightarrow ch_{p,num}\)。

4. \(last \rightarrow ch_{p,num}\) ，若是还有字符则回到 2。

其中第 2 步与 KMP 中不断跳前缀函数寻找一个可行 Border 是类似的，都是不断跳函数找到一个状态使得它满足前面一个字符与当前相等；第三步中不能把最后的两步赋值提前，否则有可能会在跳失配指针的时候进入死循环。

应用

由定义可知回文自动机的状态数等于字符串中本质不同回文串个数（排除根节点）。

每个回文子串的出现次数可以类似 ACAM 查询字符串出现次数，将每个前缀的最长回文后缀所标的状态的 \(cnt\) 加 1，接着以失配指针为边拓扑排序，则 \(cnt_u = \Sigma_{fail_v=u} cnt_v\)。

slink 链与回文划分

最小回文划分：给定一个字符串 \(s\)，求一个最小的 \(k\)，使得 \(s=t_1t_2\cdots t_k\) 并且任意 \(t\) 为回文串。

考虑一个朴素的 dp，\(f_i\) 表示 \(i\) 前缀的最小回文划分，则 \(f_i=1+\min f_j\) 且 \(s[j+1,i]\) 为回文串，时间复杂度为 \(O(n^2)\)

可以注意到每次我们转移对象都相当于扣掉了当前字符串的一个回文后缀，即为回文自动机上对应状态跳失配指针所能跳到的节点的相反部分，但是在自动机上转移仅能优化常数，我们需要一个更好的方法。

注意到一个性质：每一个回文串的回文后缀都是该串的 Border，而一个串的 Border 又可以划分为 \(O(\log n)\) 个等差数列，我们能否把回文后缀转化成 Border 利用 Border 相关性质处理呢？为了利用这个性质，我们引入 \(diff\) 函数和 \(slink\) 链

使 \(diff_u \leftarrow len_u - len_{fail_u}\)，而 \(slink_u\) 则表示沿失配指针能跳到的第一个 \(diff_v \neq diff_u\) 的节点 \(v\)，考虑新增字符后新增状态所在的等差数列发生了什么变化，如图所示（图源 oi-wiki）：

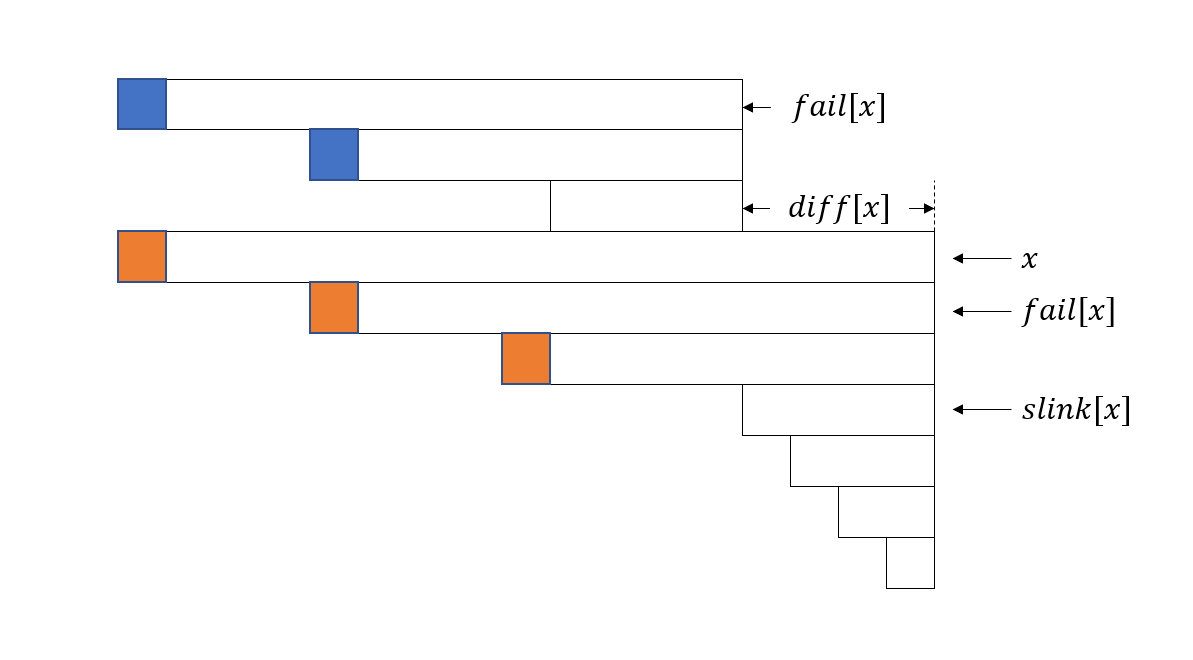
在这幅图中，同一列上的节点或线段表示在原字符串中位置相同，可以看到 \(x\) 是我们增添了一个字符后创造的状态，而它的失配指针所指向的状态在原先已经存在过，即为上面蓝色部分的 \(fail_x\)。

我们发现橙色部分与蓝色部分的答案其实只差最右边橙色块的 \(f\)，考虑设计 \(g_x\) 表示 \(x\) 到 \(slink_x\) 之前部分 \(f\) 的和，对于 \(fail_x\) 来说就是蓝色部分的 \(f\) 值求和，那么我们只要让 \(g_{ fail_x } + f_{i-diff_x-slink_x} \rightarrow g_x\) 即可，式子中的 \(f\) 就是新加的最右边的橙色部分，\(i\) 表示目前新加的字符位置，\(x\) 表示新加字符在自动机中的状态，二者比较容易弄混。

而对于其他的等差数列，我们只要继续跳 \(slink_x\) 处理即可，时间复杂度 \(O(n \log n)\)。

例题： CF932G Palindrome Partition

5.后缀树 / 后缀自动机（SAM）

后缀树

刻画子串的一个方式是将子串描述为该字符串后缀的前缀，而前后缀通常易于描述，可以考虑根据这点建立一个描述子串的结构，具体地，我们将一个字符串的所有后缀建立一棵 trie，这称为字符串 \(s\) 的后缀字典树。

这样建出的树的节点数是 \(O(n^2)\) 的，为了进一步简化，我们将树上度数为 2，即在一条长链中的节点缩到边上，使得节点之间的转移由一个字符变为了一个字符串，并且所有非叶子结点至少有两个孩子。缩点后，这颗树相当于是所有后缀终止节点的虚树，故节点数变成了 \(O(n)\)。

在后缀树上，给定一个节点和一条出边及其长度，就可以唯一确定一个字符串并它是原串的一个子串，只要从根节点向下走到对应节点，并向该出边走对应长度（边上缩了很多字符，走长度可理解为把边展开后往下走）即可求出对应子串。并且，后缀字典树上任意两个节点 LCA 表示的字符串，正是这两个节点表示的字符串的 LCP。

由于一个字符串的后缀树与其反串 SAM 的 Parent tree 同构，因此我们常常用这种方式建立后缀树，而 Ukkonen 算法也是一种增量构造后缀树的算法，有兴趣的读者可以自行查阅资料了解。

SAM 的结构

读者可以看到由于在后缀树中节点被缩起来了，我们并不能很好地接收和处理每一个子串，为此，我们先引入后缀自动机，而读者可以在介绍中看到二者的相似性。

首先，我们引入一个子串的 endpos 集合，表示这个子串在字符串中每次出现的最右端点的一个集合，例如，\(\texttt banana\) 的一个子串 \(\texttt na\) 的 endpos 集合为 \(\{4,6\}\)，我们把每个不同的 endpos 集合建立节点，而每个节点也代表 endpos 集合为当前节点所代表集合的子串。

可以发现，这样处理后节点数一定是 \(O(n)\) 的，因为 endpos 集合只可能包含不可能相交，因此你可以理解成集合的不交划分，对于每个节点，我们将包含它（endpos 集合包含它）且集合大小最小的节点设为其父亲，再将没有父亲的节点的父亲连到一个虚拟节点上，这个虚拟节点可以理解为空串代表的节点，这样，我们就建立了一棵 Parent tree。

Parent tree 的每个节点都代表着若干个 endpos 相同的字符串，一个节点上所有的字符串都是节点上长度最大的字符串的后缀，画图即可理解，定义 \(len_i\) 表示节点 \(i\) 上字符串最大的串长度。而对于 \(s1\) 为 \(s2\) 的后缀，\(\operatorname endpos(s1) \subset \operatorname endpos(s2)\)。

SAM 还有一部分转移边，对于每个节点 \(i\)，若是其上的字符串添加一个字符 \(c\) 后的字符串也为原串子串，那我们添加一条由 \(i\) 指向承载新字符串的节点的转移边，边权为 \(c\)。加上转移边，我们就得到了一棵完整的 SAM。

构造 SAM

6.参考资料

[OI wiki 自动机]( 自动机 - OI Wiki (oi-wiki.org) )

[字符串技术巡礼 - ix35]( 字符串技术巡礼 - ix35_ 的博客 - 洛谷博客 (luogu.com.cn) )

[「学习笔记」回文树（回文自动机） - zhylj]( 「学习笔记」回文树（回文自动机） - zhylj 的博客 )