P9073 [WC/CTS2023] 楼梯 题解
简要题意
有一块楼梯,这里指的楼梯是倒着的,正过来看上一层宽度一定小于等于这一层宽度,并且由格子组成,你需要对其进行增删和恢复某一历史版本的操作,并回答这块楼梯是否有固定格数的子楼梯。
题目分析
看到题目,平面,带修改查询,范围 \(10^9\),真是 buff 叠满了,似乎非常难以入手。
从特殊性质条件入手呢?此题给了很多特殊的性质,但是从它们相关的适用范围入手似乎都不是很好考虑,我们只好退而求其次,想想我们有什么能用的思考方式。
首先考虑归约问题,把题目中一些难以入手的问题转化为已知问题,本题中最大的难点就在于修改是对于整个平面的,况且范围过大,无法使用数据结构进行维护。
我们从较为简单的修改开始考虑,构造几个楼梯试着改一改,可以发现在这种更改信息下,貌似只是对于某个行区间的列数进行了区间增加,从这点出发,就可以把删的操作分解,看做区间推平和区间减法,即可把修改变为对于一个线段树的维护。
那最重要的询问呢,发现无处入手,我们换种思考方式,想想怎么简化问题,因为有了因数这一重要的约束条件,我们从小范围入手,看看能不能从一些特殊规律方面进行简化。先看当 \(p=q/2\) 时会发生什么,看题目所给的图,发现可行解的边界左端点构成了一个区间,这是不是我们想要的性质呢?
继续构造数据,发现虽然上述性质被否定了,但是可以发现另外一个性质,好像一个楼梯中总有一个以最右上方或左下方格子为边界的解,不要慌,想想我们能不能证明它。
边界边界,有什么性质吗,通过刚才的一通操作,再结合初看题目时的生成格,想必大家也能发现一个明显的条件,把生成格看做一个激光发射器,它垂直或平行射出的射线一定是穿透的,且它的楼梯所有的格子都在这里面,也就是说,一个子楼梯把左边界和上边界排除,一定是右边界开下边界结束(可能有点抽象,可以看图理解一下),而刚才说到的那两个格子贡献的也刚好是这两个边界!
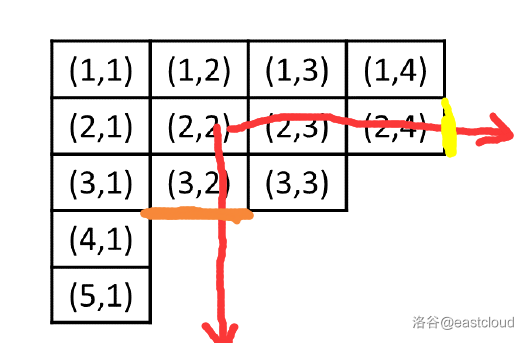
再反过来看,两个这样的边界甚至可以确定一个唯一的子楼梯!而边界的集合也可以排出一个序列,也可以我们像刚才那样维护修改,转化成边界后,看似无用的因数一条件也可以派上用场了。
继续证明上述结论,可以发现在 \(p=q/2\) 时,子楼梯另外一个边界序号都相同,要是不是上边界就配合下面的,否则可以跟上面的配对,能继续推广吗,发现这个操作本质上是一种范围的缩小,当 \(qk=p\) 时,每次通过取中点可以排除一半的区间,进而找到答案。
上述操作也能在维护边界的线段树上二分实现,于是,我们通过常用的思维模式,解决了这道看似复杂的思维问题,希望读者在做题时,也可以多尝试用归约,分解,简化等方式进行思考(这实际上摘自《线性代数入门》中的绪论部分,感觉蛮有效的就搬过来了)。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxn 1000000000
#define ll long long
#define N 300005
using namespace std;
ll tot,rt[N];
struct Node{
ll ls,rs,sum;
#define ls(x) tr[x].ls
#define rs(x) tr[x].rs
#define s(x) tr[x].sum
}tr[N<<5];
ll read(){
ll x=0,f=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
void change(ll &x,ll l,ll r,ll p,ll val){
ll np=x;x=++tot;tr[x]=tr[np];s(x)+=val;
if(l==r) return;
ll mid=(l+r)>>1;
if(p<=mid) change(ls(x),l,mid,p,val);
else change(rs(x),mid+1,r,p,val);
s(x)=s(ls(x))+s(rs(x));
}
ll query(ll x,ll l,ll r,ll L,ll R){
if(!x || (L>=l && R<=r)) return s(x);
ll mid=(L+R)>>1;ll ans=0;
if(l<=mid) ans+=query(ls(x),l,r,L,mid);
if(r>mid) ans+=query(rs(x),l,r,mid+1,R);
return ans;
}
void clear(ll &x,ll l,ll r,ll L,ll R){
if(!x) return;if(L>=l && R<=r){x=0;return;}
ll np=x;x=++tot;tr[x]=tr[np];
ll mid=(L+R)>>1;
if(l<=mid) clear(ls(x),l,r,L,mid);
if(r>mid) clear(rs(x),l,r,mid+1,R);
s(x)=s(ls(x))+s(rs(x));
}
ll find_pos(ll x,ll l,ll r,ll val){
if(l==r) return l;
ll mid=(l+r)>>1;
if(s(rs(x))>=val) return find_pos(rs(x),mid+1,r,val);
else return find_pos(ls(x),l,mid,val-s(rs(x)));
}
ll find_x(ll x,ll val,ll l,ll r){
if(l==r) return val==1?l:-l;
ll mid=(l+r)>>1;
if(mid-l+1+s(ls(x))>=val) return find_x(ls(x),val,l,mid);
else return find_x(rs(x),val-(mid-l+1)-s(ls(x)),mid+1,r);
}
void solve(ll val,ll l,ll r,ll rt){
if(l==r-1){
ll p=find_x(rt,l*val+1,1,maxn),q=-find_x(rt,r*val+1,1,maxn);
cout<<p<<' '<<query(rt,p,maxn,1,maxn)-(val+p-q)+1<<endl;
return;
}
ll mid=(l+r)>>1;
if(find_x(rt,mid*val+1,1,maxn)>0) solve(val,mid,r,rt);
else solve(val,l,mid,rt);
}
int main(){
ll m,a,b;char opt;
m=read();
for(ll i=1;i<=m;i++){
rt[i]=rt[i-1];
cin>>opt;a=read();
if(opt=='+'){b=read();change(rt[i],1,maxn,a,b);}
else if(opt=='R') rt[i]=rt[i-a-1];
else if(opt=='-'){
b=read();
ll sum=query(rt[i],a,maxn,1,maxn);
if(sum<b){
clear(rt[i],a,maxn,1,maxn);
if(a!=1) change(rt[i],1,maxn,a-1,sum);
}
else{
ll p=find_pos(rt[i],1,maxn,b);
ll tmp=query(rt[i],p+1,maxn,1,maxn);
clear(rt[i],p+1,maxn,1,maxn);
change(rt[i],1,maxn,p,tmp-b);
if(a!=1) change(rt[i],1,maxn,a-1,b);
}
}
else if(opt=='?'){
if(s(rt[i])==0){cout<<-1<<' '<<-1<<endl;continue;}
ll k=find_pos(rt[i],1,maxn,1);
ll sum=k-1+s(rt[i]);
solve(a,0,sum/a,rt[i]);
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号