网络流24题学习笔记
前言
众所周知,网络流是一种可以解决多种复杂问题的算法,其核心就在于对于问题进行简化并抽象成图,再通过网络流的一个个模型进行求解。
本篇则通过网络流24题,网络流中较为经典的题型入手,对于题目的思考过程和技巧进行分析,丰富模型并促进思维方面的提高。
网络流
0x01 P1251 餐巾计划问题
题意:一个饭店每天要用一些餐巾,既可以买新的也可以每天晚上送去洗,洗餐巾分为快洗和慢洗,有不同的价格和时间,求最少用多少钱能满足条件。
如何判断一个题目属不属于网络流呢,从这题的角度出发,可以归纳出几个明显特征:
- 有“求最大”,“最小花费”等明显字眼
- 可以将题目中的操作简化为图中的边与点
- 有对于操作关于数量方面的限制
对于此题,既有花费最小,可简化,有数量的限制三个符合条件,我们便可以思考是否可以用网络流中的费用流解答。
我们将题目所给的信息简化,将每一天变为点,输送餐巾的过程变为边,餐巾数量变为容量,价格变为费用,根据题中所给信息建图,尝试此种方式是否可行。失败,我们发现这种方式存在两个缺点,第一个为无法准确表示干净和脏餐巾两种状态,如将脏餐巾直接输送的话因为费用计算了两次会不如当天购买优,第二个为餐巾可以重复使用,但是网络中的流却不能复制。
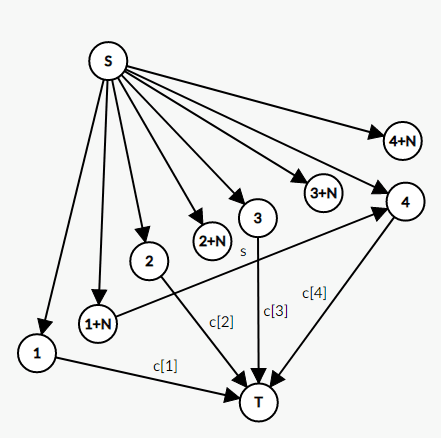
分别考虑两个问题的处理方式,对于第一个,我们利用网络流建模中常用的拆点,将一天分为用前与用后两个点,避免混淆,而第二个问题我们则改变建边方法,思考题目可以得出,无论我如何变幻,每天一定会新产生 \(cost[ i ]\) 条脏餐巾,我们便将用前变为花费点,用后变为产生点,花费点既可以从源点处直接获取费用为 $ p $ 的餐巾,也可以从前几个点的产生点处“洗”来餐巾,而产生点则可以从源点处获取免费的旧餐巾(固定条数),最后再将花费点与汇点连边,由于旧餐巾是免费的的,便可以不考虑餐巾重复使用的情况。另外还需将每天的产生点与下一天的产生点连边,保证旧餐巾的延后送洗,图示如下(用 \(i\) 与 \(i+N\) 表示花费点与产生点 )。
点击查看代码
// Problem: P1251 餐巾计划问题
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1251
// Memory Limit: 125 MB
// Time Limit: 4000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define ll long long
#define inf 1<<30
using namespace std;
ll head[1000001],to[1000001],edg[1000001],cost[1000001],nex[1000001];
ll d[1000001],pre[1000001],incf[1000001],val[1000001],vis[1000001];
ll tot=1,s=0,t,ans;
queue<ll> q;
void add(ll u,ll v,ll c,ll w){
edg[++tot]=c;cost[tot]=w;to[tot]=v;nex[tot]=head[u];head[u]=tot;
edg[++tot]=0;cost[tot]=-w;to[tot]=u;nex[tot]=head[v];head[v]=tot;
}
bool spfa(){
for(ll i=s;i<=t;i++) d[i]=inf;
for(ll i=s;i<=t;i++) vis[i]=0;
d[s]=0;q.push(s);vis[s]=1;
incf[s]=inf;
while(q.size()){
ll u=q.front();q.pop();vis[u]=0;
for(ll i=head[u];i;i=nex[i]){
ll v=to[i];
if(!edg[i]) continue;
if(d[v]>d[u]+cost[i]){
d[v]=d[u]+cost[i];
if(!vis[v]){
q.push(v);
vis[v]++;
}
pre[v]=i;
incf[v]=min(edg[i],incf[u]);
}
}
}
if(d[t]==inf) return false;
return true;
}
void dfs(){
ll x=t;
while(x!=s){
ll i=pre[x];
edg[i]-=incf[t];
edg[i^1]+=incf[t];
x=to[i^1];
}
ans+=(d[t]*incf[t]);
}
int main(){
ll N,p,m,f,n,si;
cin>>N;
t=2*N+2;
for(ll i=1;i<=N;i++)cin>>val[i];
cin>>p>>m>>f>>n>>si;
for(ll i=1;i<=N;i++){
add(s,i,inf,p);
add(i,t,val[i],0);
add(s,i+N,val[i],0);
if(i+m<=N) add(i+N,i+m,inf,f);
if(i+n<=N) add(i+N,i+n,inf,si);
if(i+1<=N) add(i,i+1,inf,0);
}
while(spfa()) dfs();
cout<<ans;
}
0x02 P2754 [CTSC1999]家园 / 星际转移问题
题意:给定飞船的航班,中转站个数,飞船载客量,求出从地球运 \(k\) 个人到月球最少需要多久。
首先,题中给出了人数,求时间,我们发现“最少”通常使用最小费用最大流,但是本题却并不好求解,我们可以转换思路,改求解为验证,枚举时刻(不用二分是因为网络流在残量网络上寻找增广路时效率更高),考虑当前时刻能否满足人数要求,易得出我们可以将飞船载客量变为容量,求出当前网络的最大流即为当前时刻的最大人数。
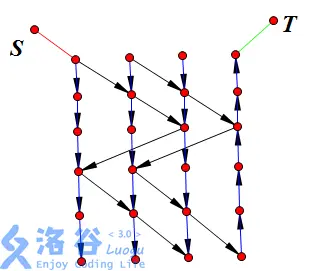
根据题中给出信息直接建边,再将地球与月球分别当做源点和汇点,判断是否能满足条件,我们发现站与站之间的时间关系没办法很好体现,例如可能会出现有的中转站实际使用次数不如理论的情况,因为当有时候飞船到来时站点还没人能到达,那如何结合时间这一变量呢,考虑到边都是在不同的时间的点中进行连接,我们可以引入分层图,将点根据时间分层,再在层之间连边,将源点设为最低的地球,汇点设为最高的月球(这里指分层图中的时间),跑最大流即可,图示如下(引用自洛谷 Adove)
点击查看代码
// Problem: P2754 [CTSC1999]家园 / 星际转移问题
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2754
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define ll long long
#define inf 1<<29
using namespace std;
int val[41][40],cont[41],f[41];
int head[1000001],to[1000001],nex[1000001],cur[10000001],edg[1000001];
int d[1000001];
int tot=1,now,N,maxflow,s=0,T=13000;
queue<int> q;
int find(int x){
if(f[x]==x) return x;
else return f[x]=find(f[x]);
}
void merge(int x,int y){
x+=2;y+=2;
x=find(x);y=find(y);
if(x!=y) f[x]=y;
}
bool bfs(){
for(int i=0;i<=(now+1)*N;i++) d[i]=0;
for(int i=0;i<=(now+1)*N;i++) cur[i]=head[i];
d[T]=0;cur[T]=head[T];
while(q.size()) q.pop();
d[s]=1;q.push(s);
while(q.size()){
int u=q.front();q.pop();
for(int i=head[u];i;i=nex[i]){
int v=to[i];
if(!edg[i]) continue;
if(!d[v]){
d[v]=d[u]+1;
q.push(v);
if(v==T) return true;
}
}
}
return false;
}
int dfs(int x,int flow){
if(x==T) return flow;
int rest=flow,k;
for(int i=cur[x];i && rest;i=nex[i]){
cur[x]=i;
int v=to[i];
if(edg[i] && d[v]==d[x]+1){
k=dfs(v,min(edg[i],rest));
if(!k) d[v]=0;
rest-=k;
edg[i]-=k;
edg[i^1]+=k;
}
}
return flow-rest;
}
void add(int u,int v,int c){
edg[++tot]=c;to[tot]=v;nex[tot]=head[u];head[u]=tot;
edg[++tot]=0;to[tot]=u;nex[tot]=head[v];head[v]=tot;
}
int main(){
int n,m,t;
cin>>n>>m>>t;
for(int i=1;i<=n+2;i++) f[i]=i;
N=n+2;
for(int i=1;i<=m;i++){
cin>>cont[i]>>val[i][0];
for(int j=1;j<=val[i][0];j++)cin>>val[i][j];
for(int j=1;j<val[i][0];j++) merge(val[i][j],val[i][j+1]);
if(val[i][0]!=1 || val[i][0]!=2) merge(val[i][1],val[i][val[i][0]]);
}
if(find(1)!=find(2)){
cout<<0;
return 0;
}
for(int i=1;i<=m;i++)for(int j=1;j<=val[i][0];j++)val[i][j]+=2;
add(1,T,inf);add(s,2,inf);
for(int ans=1;;ans++){
now=ans;
for(int i=1;i<=n+2;i++) add(i+N*(ans-1),i+N*ans,inf);
add(N*ans+1,T,inf);add(s,N*ans+2,inf);
for(int j=1;j<=m;j++){
if(val[j][0]==1) continue;
int k=(ans%val[j][0])+1;
int l=(k-1+val[j][0])%val[j][0];
if(l==0) l=val[j][0];
add((ans-1)*N+val[j][l],val[j][k]+N*ans,cont[j]);
}
while(bfs()){
while(1){
int flow=dfs(s,inf);
if(!flow) break;
maxflow+=flow;
}
}
if(maxflow>=t){
cout<<ans;
return 0;
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号