AI-Adversarial Search
博弈 Game 的分类维度
- Deterministic or stochastic?
- One, two, or more players?
- Zero sum?
- Perfect information (can you see the state)?
Adversarial Search
对抗搜索 Adversarial Search 关注的是 perfect information, deterministic, two players, zero-sum, alternate turns 的博弈。典型的例子有 Tic-tac-toe, chess, Go, Gomoku 等。
在双人博弈的场景下,由于是零和游戏一方分数为正,则另一方则必为相应的负数。这样的话,我们可以给场上的局势统一「打分」,一方欲求最大化该分数,而另一方意图最小化该分数。例如对 MAX 节点来说
这样的话,我们给出 Minimax Search 的定义:
A state-space search tree. Players alternate turns
Compute each node’s minimax value: the best achievable utility against a rational (optimal) adversary
具体到算法层面,对于一个特定的节点,我们可以给出一个统一的求其值的形式
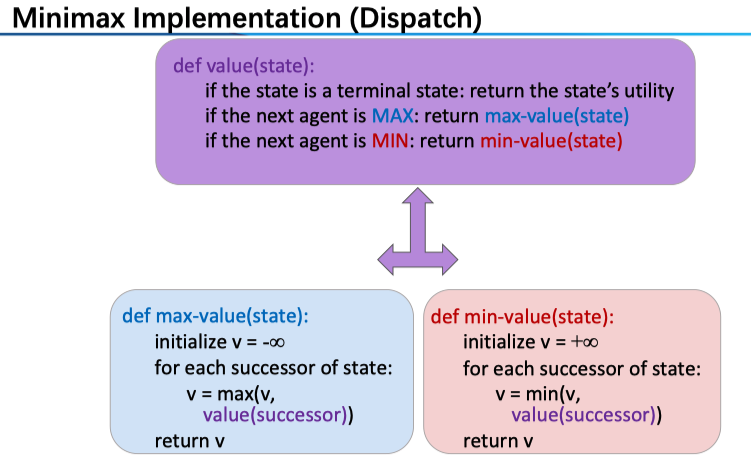
对于一个 MAX 节点来说,玩家希望最大化分数,所以肯定会选择最有利的那一个策略(后继中分数最高的),对于 MIN 节点同理。
Note:我们对于「局势」的打分一般不是根据最终的结果来决定的(例如若 A 胜利则给 1,A 负则设为-1),因为受到资源的约束我们没法搜索很深(显然会采用 DFS,时间空间复杂度分别为 \(O(b^m )\), \(O(bm)\),对于 chess 来说,b 约为 35,m 约为 100);所以我们会给中间节点基于场上的「形势」打分,也就是说,我们采用的是 Depth-limited search,限制了搜索深度,需要 Evaluation function 对于 non-terminal positions 评分。当然,算法给出的策略的 optimal 无法保障;我们总希望越深越好,所以可以采用 iterative deepening 的策略。对于 Evaluation function 来说,理想的显然是返回这一状态的真实「价值」,但其计算就会变得相当复杂,因此其体现的是 tradeoff between complexity of features and complexity of computation;对于其我们的要求有
- Utility for a win state should be higher than a tie. (correct)
- The computation of evaluation function should be efficient. (quick)
- It should be related to the chance of wining the game. (consistent)
Game Tree Pruning
当然是最有名的 Alpha-Beta Pruning 了。其想法非常简单(然而,在具体实现中代码有难度,所以我们详细讲一下):对于一个 MAX 节点来说,若其第一个子节点 A 返回的是 3,那么对于第二个子节点 B(注意是 MIN 节点),若 B 的第一个子节点返回的是 2,那么我们可以确定 B 的值肯定要 ≤2(因为 B 为 MIN 节点),也就必 ❤️,因此我们没有必要继续探索 B 的剩余子节点了。
注意到,上述是对于 MIN 节点进行的剪枝,MIN 的子节点返回的一个值与其维护的一个值(\(\alpha\))进行比较,若小于了这个值则直接将此 MIN 节点剪去不去看齐剩下的子节点。上述只是一个特例,下图是一般情况

这里的逻辑是这样的:在之前的例子中我们只关注了 MIN 的父 MAX 节点,事实上我们可以「看」得更远(剪枝也就更有效率),也就是这里标识出来的两个 MAX 节点,实际上是一条 MAX 节点序列,为什么可以这样呢?这里要注意我们所维护的 \(\alpha\) 的含义,它是这条路径上 MAX 节点的最优选择。
对于 MIN 节点 n 来说,一方面,它要从它的子节点这里选出最小的那一个(Note:我们结合下图中右边的伪码来看),也就是算法中的 v,若这个值小于了 \(\alpha\) ,即这条路径上 MAX 节点的最优选择(标红行),那么我们直接返回 v(对于该 MIN 节点值的一个保守估计)。那么,关键在于 \(\alpha\) 究竟是从哪里来的呢?我们来看算法中左边的 MAX 节点的操作(注意,对于 \(\alpha\) 的更新只在 MAX 节点进行):\(\alpha=\max(\alpha, v)\) 。分开来讨论,若 1. max 取到的是 v,那么 \(\alpha\) 就表示了该 MAX 节点在 for 循环中取到的最优结果(此前的子节点中的最优结果),在下一个循环中我们在标紫行调用了子节点的 min-value,即右边的算法;2. max 取到的 \(\alpha\) 来自本身传入 max-value 中的那个值(这里我们结合上图),也就是这条路径之上的 MAX 节点的最优选择,比如说,对于上面的那个蓝色 MAX 节点 A,我们在其左孩子取到了 3,我们把这个 \(\alpha\) 值传给了 n 的父 MAX 节点 B:老大 A 告诉小弟 B:我另一个小弟已经献给我 3 了,你如果比这个值小就甭给我拿出来丢人了,于是 B 也会拿这个 \(\alpha\) 来给其子 MIN 节点进行剪枝(也就是右边算法中标红的操作)。另一方面,MIN 节点要维护一个\(\beta\) :该条路径下 MIN 节点的最优选择,分析和上述是相一致的。
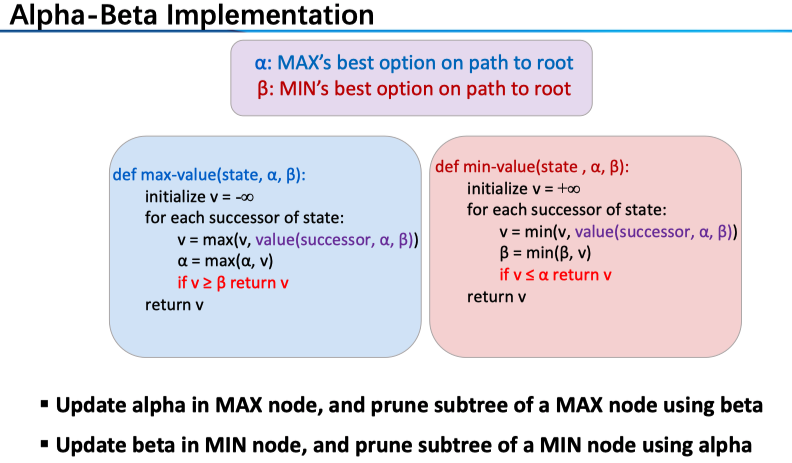
上图总结得真的完美,若还有不懂的再多看两遍,或者画一棵树自己跑一下吧。对于 alpha-beta 剪枝我们有如下说明:1. This pruning has no effect on minimax value computed for the root. Minimax values of intermediate nodes might be wrong. 对于根节点来说,我们初始化 \(\alpha=-\infty, \beta=+\infty\) 并进行搜索,注意到 alpha-beta 剪枝仅仅是把一些肯定对结果没有影响的节点删去了,因此不会影响最终的值;然而,对于中层的节点来说,alpha-beta 剪枝所给出值是在减去了一些分支的情况下得到的,这样给出的「分数」就可能不是其真值了。2. Ordering Matters 显然,若所有可剪的分支都排在最后那么对于最终的效率就没什么影响了,一般情况下,alpha-beta 剪枝可以Doubles solvable depth!
Uncertain Outcomes
主体就这些内容,后面介绍了一下非确定情况下的节点,增加了随机性:例如玩家是非理性的,或游戏本身就有随机性如 Dice,这样的话我们可以取期望。
Utilities
这部分更多是简单抽象的博弈中超脱了出来,毕竟这种情况是确定的理想的;事实上,相同的结果对于不同人的价值是不一样的,也就是效用这一概念的由来。
Utilities are functions from outcomes (states of the world) to real numbers that describe an agent’s preferences
In a game, may be simple (+1/-1)
Utilities summarize the agent’s goals
Theorem: any “rational” preferences can be summarized as a utility function
注意,我们这里讨论的并非上述的双方博弈,而是 Maximum Expected Utility 算法
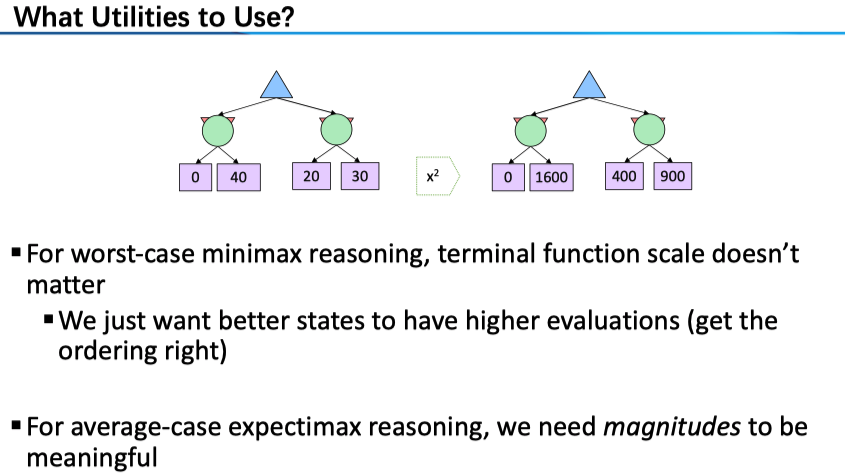
最后再对 Utilities 的概念做一点说明,正如定义中所说它反映的是一个人的 preferences ,相较于简单的 outcomes 更具有现实性,例如一个不爱冒风险的人和一个赌徒的偏好是不同的。另外,很少有人的真正理性的,例如:Famous example of Allais (1953)
A: \([0.8,\$4k; 0.2,\$0]\)
B: \([1.0, \$3k; 0.0, \$0]\)C: \([0.2, \$4k; 0.8, \$0]\)
D: \([0.25, \$3k; 0.75, \$0]\)
Most people prefer B > A, C > D
然而,人是否真的是理性的呢?假若 \(U(\$0) = 0\),那么 B > A 可推出 \(U(\$3k) > 0.8 U(\$4k)\),而 C > D 则可推出 \(0.8 U(\$4k) > U(\$3k)\)——出现了两个矛盾的结果。
一下仅仅是个人感想:我们假定 utility 正是回报,那么这里例子深刻地反映了人对于概率/数字并不敏感。对于 A 和 B,3k 和 4k 刀差别不大,我们可能出于厌恶风险的原则选 B;对于 C 和 D,两者都有一定的风险,而我们对于 .2 和 .25 的区别并不敏感,这时候 4k 和 3k 刀的差距就显现出来,也就更倾向于选大一点的 C(虽然这时是一个正确的选择)。





