浅谈Palindromic Tree——回文树（回文自动机）

回文树的主要功能如下

1.求串S前缀1~i内本质不同回文串的个数（两个串长度不同或者长度相同且至少有一个字符不同便是本质不同）

2.求串S内每一个本质不同回文串出现的次数

3.求串S内回文串的个数（其实就是1和2结合起来）

4.求以下标i结尾的回文串的个数,从以下标i开头的也可以，倒着做一遍就行

回文树有两个特殊的节点0号节点和一号节点分别对应了空串和长度为−1的串，是为了添加只有一个字符和两个字符的回文串时更方便，减少特判。

有个结论是：一个字符串ss本质不同的回文串个数是O(n)的，所以回文树中的节点数也是O(n)的。

一开始回文树有两个节点，0表示偶数长度串的根和1表示奇数长度串的根，且len[0] = 0，len[1] = -1，last = 0，S[0] = -1，n = 0，p = 2（添加了节点0、1）,fail[1]=1,fail[0]=1。

空间复杂度为O（N*字符集大小），时间复杂度为O（N*log（字符集大小））

假如一个字符的流程如下
假如我们添加一个字符s[i]='a'，S[++ n] = 'a'，然后判断此时S[n - len[last] - 1]是否等于S[n]，即上一个串（last指针在匹配过程中指向的串可以认为是以i-1位置为结尾的尚未尝试匹配的最长后缀回文串）-1的位置和新添加的位置是否相同，相同则说明构成回文。否则沿着fail指针走，last = fail[last]，直到S[n - len[last] - 1]等于S[n]为止，当然也不会一直走下去，当last为1的时候必满足，因为单个字符必能构成一个长度为1的回文，len[1]等于-1可以让这一步更加方便.
令cur等于此时的last（即cur = last = 1），判断此时next[cur]['a']是否已经有后继，如果next[cur]['a']没有后继，我们就进行如下的步骤：新建节点（节点数p++，且之后p = 3），并让now等于新节点的编号（now = 2），则len[now] = len[cur] + 2（每一个回文串的长度总是在其最长子回文串的基础上在两边加上两个相同的字符构成的，所以是+2，。然后我们让fail[now] = next[get_fail ( fail[cur] )]['a']（连fail边，fail边指向的是now节点的回文串的最长后缀回文串），其中的get_fail函数就是让找到第一个使得S[n - len[last] - 1] == S[n]的last。然后next[cur]['a'] =now(连next边)。
当上面步骤完成后我们让last = next[cur][c]（不管next[cur]['a']是否有后继），然后cnt[last] ++。

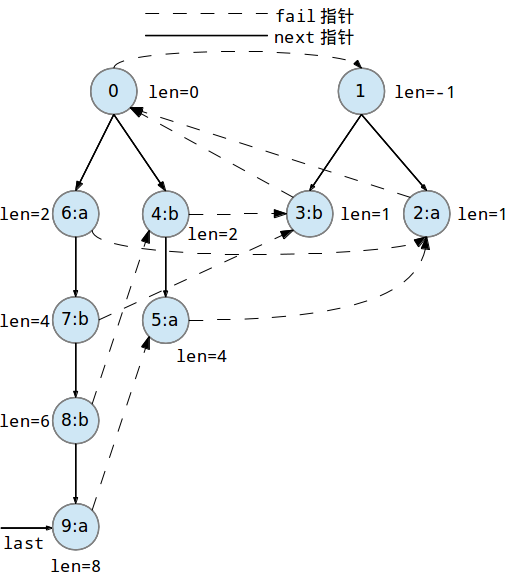
abbaabba构建的回文树

 

http://acm.hdu.edu.cn/showproblem.php?pid=5157

题意：统计一个字符串中不相交的回文串的对数。

利用了num[last]即以i位置的字符为尾的回文串个数的性质，先预处理出pre[i]表示以1~i位置为尾的回文串个数，然后倒着处理一遍，对 pre[i]*以i+1位置为头的回文串个数 求和即可

#include<bits/stdc++.h>
using namespace std;
#define ls rt<<1
#define rs (rt<<1)+1
#define ll long long
#define fuck(x) cout<<#x<<"     "<<x<<endl;
const int maxn=1e5+10;
const ll mod=1e9+7;
int d[4][2]={1,0,-1,0,0,1,0,-1};
char s[maxn];
ll pre[maxn];
const int MAXN = 1e5+10;//长度
const int N = 26;//字符集大小
struct Palindromic_Tree {
    int next[MAXN][N];//next指针，next指针和字典树类似，指向的回文子串为i节点对应的回文子串两端加上同一个字符ch构成
    int fail[MAXN];//fail指针，失配后跳转到fail指针指向的节点，fail指针指向的是i节点对应的回文子串的最长后缀回文子串（是真后缀），这个匹配过程与kmp有点类似，fail[i]表示节点i失配以后跳转到长度小于该串且以该节点表示回文串的最后一个字符结尾的最长回文串表示的节点
    int cnt[MAXN];//在调用count函数之后，cnt[i]表示i节点对应的回文子串的出现次数的准确值
    int num[MAXN];//在调用add函数之后返回num[last]可以得到以i位置的字符为尾的回文串个数
    int len[MAXN];//len[i]表示节点i表示的回文串的长度
    int S[MAXN];//存放添加的字符,
    int last;//指向上一个字符所在的节点，方便下一次add
    int n;//字符数组指针，从1开始，到n结束
    int p;//节点指针，0指向偶根，1指向奇根，有效编号到p-1

    int newnode(int l) {//新建节点
        for (int i = 0; i < N; ++i) next[p][i] = 0;
        cnt[p] = 0;
        num[p] = 0;
        len[p] = l;
        fail[p]=0;
        return p++;
    }

    void init() {//初始化
        p = 0;
        newnode(0);
        newnode(-1);
        last = 0;
        n = 0;
        S[n] = -1;//开头放一个字符集中没有的字符，减少特判
        fail[0] = 1;
    }

    int get_fail(int x) {//和KMP一样，失配后找一个尽量最长的
        while (S[n - len[x] - 1] != S[n]) x = fail[x];
        return x;
    }

    int add(int c) {
        c -= 'a';
        S[++n] = c;
        int cur = get_fail(last);//通过上一个回文串找这个回文串的匹配位置
        if (!next[cur][c]) {//如果这个回文串没有出现过，说明出现了一个新的本质不同的回文串
            int now = newnode(len[cur] + 2);//新建节点
            fail[now] = next[get_fail(fail[cur])][c];//和AC自动机一样建立fail指针，以便失配后跳转
            next[cur][c] = now;
            num[now] = num[fail[now]] + 1;
        }
        last = next[cur][c];
        cnt[last]++;
        return num[last];
    }

    void count() {
        for (int i = p - 1; i >= 0; --i) cnt[fail[i]] += cnt[i];
        //父亲累加儿子的cnt，因为如果fail[v]=u，则u一定是v的子回文串！
    }
}pt;

int main(){
    while(scanf("%s",s+1)!=EOF) {
        ll ans = 0;
        int len;
        len = strlen(s + 1);
        pt.init();
        for (int i = 1; i <= len; i++)
            pre[i] = (pre[i - 1] + pt.add(s[i]));
        pt.init();
        for (int i = len; i >= 1; i--)
            ans += 1LL * pre[i - 1] * pt.add(s[i]);
        printf("%lld\n", ans);
    }
    return 0;
}

https://blog.csdn.net/u013368721/article/details/42100363

http://www.360doc.com/content/19/0120/11/5315_810146088.shtml