题目:点此
题目描述
在这个问题中,给定一个值S和一棵树。在树的每个节点有一个正整数,问有多少条路径的节点总和达到S。路径中节点的深度必须是升序的。假设节点1是根节点,根的深度是0,它的儿子节点的深度为1。路径不必一定从根节点开始。
输入格式
第一行是两个整数N和S,其中N是树的节点数。 第二行是N个正整数,第i个整数表示节点i的正整数。 接下来的N-1行每行是2个整数x和y,表示y是x的儿子。
输出格式
输出路径节点总和为S的路径数量。
思路
先准备数据结构:(描述思路时会用到,先给出定义和使用)
1.vector <int> tree[100000],邻接表(把树看成DAG图)
2.int a[100000]={0},前缀和数组
3.bool color[100001]={false},dfs时使用,true代表访问过,false代表没访问过
4.int weight[100000],存储权值(邻接表不存权值)
5.set <int> r,找根节点(r内的为可能是根节点的元素)
先读入n,s;再读入权值,并将i存入邻接表,权值存入weight。
接着读入x、y,将y插在tree[i]的后面并从集合r中删除y(y有双亲结点(父节点),不可能是根)
最后r中剩下的就是根,存起来(我的root变量),前缀和数组a[0]清零,接着进入dfs:(用递归)
将color[当前访问顶点编号(我的now变量)]置成true,表示已访问,接着计算该节点的前缀和*,然后找结点继续dfs,当结点访问完毕后,用二分搜索找前缀和数组中是否有a[现深度(deep)]-s(在dfs函数里设个变量名打成p了,不过没有关系),若有路径数量++。
*:见附录1
犯的错误
1.二分查找找的是a[deep]-s而不是s。
2.应该用递归实现dfs,而不是用栈,应为用递归比较熟练,不容易错。
3.树根不一定是零,需要找树根。
4.应该用weight数组存权值而不是tree[XX][0]。
收获
1.要注意前缀和:a[i]+a[i+1]+···+a[j]=(a[1]+a[2]+···+a[i-1])-(a[1]+a[2]+a[3]+a[4]+···+a[j])
2.在条件允许的情况下,要用自己熟练的方法解体。
3.不要想当然,不要有侥幸心理。
4.在n<=100000的情况下,不要怕多开几个数组。
附录一
这里用的前缀和是一条从根节点出发的路径上的前缀和
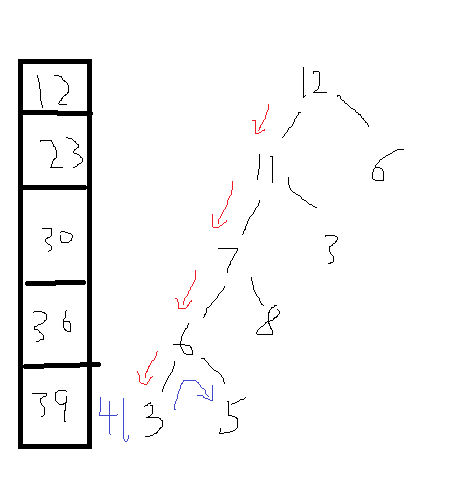
如上图,它原来的路径是12--11--7--6--3,现在变成了12--11--7--6--5,所以数组变成了12、23、30、36、41。

现在路径变成了12--11--7--8,数组变成了12、23、30、38、41。
由于数组是有序的,所以查找有没有路经总和为S是要用二分查找优化。



