对平底锅和垃圾的O奖论文的整理和学习[1](2018-02-08发布于知乎)
![对平底锅和垃圾的O奖论文的整理和学习[1]](https://pic4.zhimg.com/v2-f06468dc8a43d058060d92b5656fa432_r.jpg)
今天和杉杉同志在Pacific Coffee坐了0.4天,目前两人都处于放空状态。
这种天气有暖气真的太棒了。
我今天看的论文是这两篇:
 MCM2013B题O奖论文
MCM2013B题O奖论文 MCM2016B题O奖论文
MCM2016B题O奖论文
先说第一篇:
这篇论文给出了两个模型,一个算法。
第一个模型描述了锅边缘的热分布,第二个模型寻找了在两个假定因素(空间利用率最大,和温度分布不均程度最小)下各自的最优解。属于之前提到的有约束最优化问题。并且分析了随着平底锅的形状(边数)变化温度的变化。
题目有三个要求:
1.最大化锅的数目咋办?
2.最大化热量均匀分布咋办?
3.对1和2进行权衡怎么搞?
论文对1给出了整数规划的解法,因为锅的数目只能是整数。
对2和3给出一个算法,这个算法基于Center Dot Matrix Statistics 。就是把每个平底锅的中心拿出来,然后弄一个矩阵进行统计。
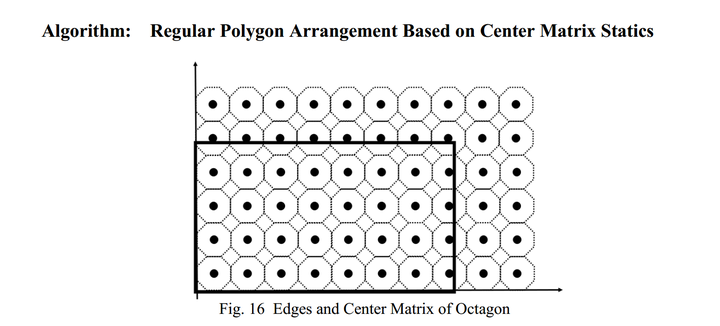 不仅整齐,而且标注完整
不仅整齐,而且标注完整
这篇论文,给我最大的感受就是美。
整洁,简洁,以及文末制作的烤炉广告的那种视觉传达效果。
全篇总共出现了31个方程式,大部分都很简短,分布在文章的各处。而排版出来的效果就是每一个方程下面都有一段解释文字,看起来很舒服。
 只给出关键的公式
只给出关键的公式
而且,文章的绘图也十分的整洁,每一个图片都很好的传达了作者得到的结果。而在广告纸中,作者把文章中通过二维绘制的图片变成了立体的图片,显得更加真实。
 虽然看不懂,但是看起来很舒服
虽然看不懂,但是看起来很舒服 暖色作为主色调,还放上一个蛋糕抓眼球
暖色作为主色调,还放上一个蛋糕抓眼球 想必这个广告单做了蛮久吧
想必这个广告单做了蛮久吧
那么,那个所谓的Regular Polygon Arrangement 是怎么实现的呢?
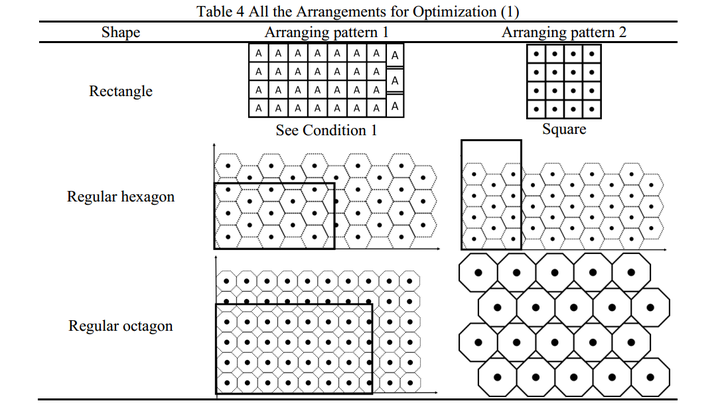
Every kind of polygon has several unique close package arranging patterns. As a result, we can draw the matrix of centers on graph paper. Make the axis overlap with edges of polygons as much as possible. Thus, we only need to determine whether the polygon with a certain center can be put inside the rectangle or the boundaries. Take rectangle rack boundaries as the example.
每一种形状有几个特别靠近的排列样式。我们可以在纸上画一个中心点的点阵,使得轴尽可能多的重叠在几何图形的边缘上面。那么,我们只需要看对应的多边形的中心点能不能被放进矩形边界就可以了。以矩形为例。(重叠的越多,说明矩形边界(烤炉的界面)内的平底锅越多,平底锅中心点也越多)。
For any point that lays inside the rectangle, it must comply the following conditions:
1. The least distance between this point and the edges of the rectangle must not be less than the radius of its inscribed circle;
2. For hexagon, the least distance between this point and the edges of the rectangle must not be less than the radius of its circumcircle;
For regular hexagon, because of that the distance between dots along x axis and along y axis are different, we need to rotate the rack 90 degree when one analysis is finished and do the analysis again, and then pick the optimal arrangement.
矩形内的每一个中心点都要满足以下要求:
1.点到边缘的最小距离不得小于内接圆半径;
2.对多边形而言,点到边界的最小距离不得小于外接圆半径;
对正多边形,因为在x轴方向和y轴方向上点的距离是不一样的,某一个分析完之后我们需要把烤架旋转90°,再对另一个进行分析,然后选择全局最优的放置策略。
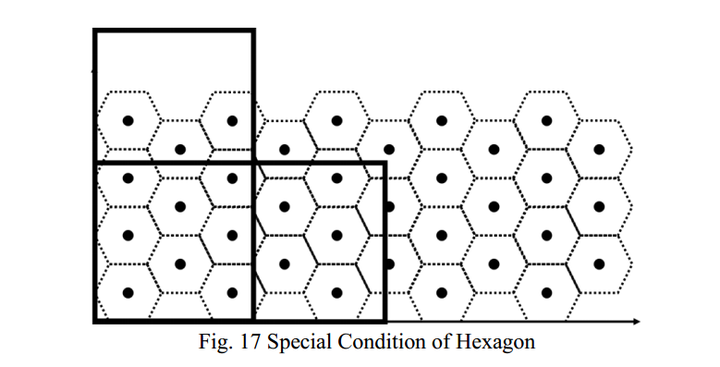 多边形的特殊情况
多边形的特殊情况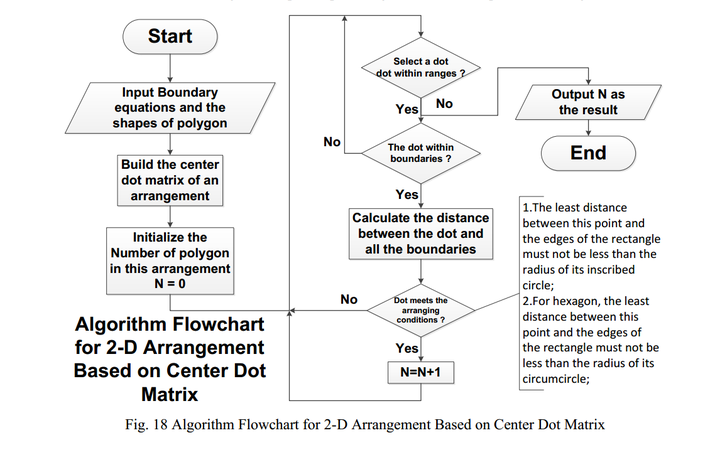 说再多都没这个流程图清晰
说再多都没这个流程图清晰
算法就是不停的判别中心点们在不在边界里面,如果遍历完了范围内的所有点,就输出烤炉里能放的平底锅个数N。


