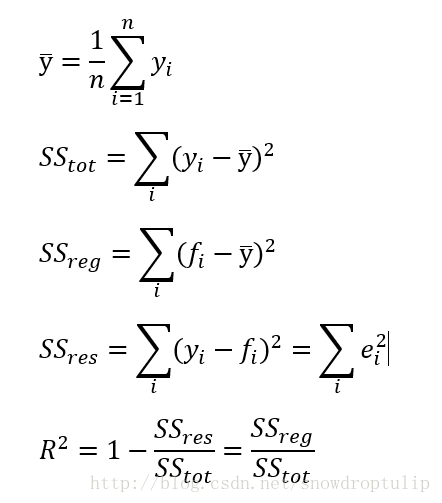数据挖掘笔记(2018-03-22发布于知乎)

 

单选题

1.哪些是基于规则的分类器？

C4.5

KNN？Bayes？ANN？C4.5？

K-NN是一种基于实例的学习，或者是局部近似和将所有计算推迟到分类之后的惰性学习。k-近邻算法是所有的机器学习算法中最简单的之一。

基于规则的分类器有如下特点：
规则集的表达能力几乎等价于决策树，因为决策树可以用互斥和穷举的规则集表示。基于规则分类器和决策树分类器都对属性空间进行直线划分，并将类指派到每个划分。然而，如果基于规则的分类器允许一条记录触发多条规则的话，就可以构造一个更加复杂的决策边界。
基于规则的分类器通常被用来产生更易于解释的描述性模型，而模型的性能却可与决策树分类器相媲美。
被很多基于规则的分类器（如RIPPER）所采用的基于类的规则定序方法非常适于处理类分布不平衡的数据集。

 

人工神经网络（英语：artificial neural network，缩写ANN），简称神经网络（neural network，缩写NN）或类神经网络，在机器学习和认知科学领域，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具。典型的神经网络具有以下三个部分：
结构（Architecture）结构指定了网络中的变量和它们的拓扑关系。例如，神经网络中的变量可以是神经元连接的权重（weights）和神经元的激励值（activities of the neurons）。
激励函数（Activity Rule）大部分神经网络模型具有一个短时间尺度的动力学规则，来定义神经元如何根据其他神经元的活动来改变自己的激励值。一般激励函数依赖于网络中的权重（即该网络的参数）。
学习规则（Learning Rule）学习规则指定了网络中的权重如何随着时间推进而调整。这一般被看做是一种长时间尺度的动力学规则。一般情况下，学习规则依赖于神经元的激励值。它也可能依赖于监督者提供的目标值和当前权重的值。例如，用于手写识别的一个神经网络，有一组输入神经元。输入神经元会被输入图像的数据所激发。在激励值被加权并通过一个函数（由网络的设计者确定）后，这些神经元的激励值被传递到其他神经元。这个过程不断重复，直到输出神经元被激发。最后，输出神经元的激励值决定了识别出来的是哪个字母。

 

 

2.K均值与DBSCAN比较？

基于密度聚类的DBSCAN和kmeans算法比较 - kongmeng - 博客园​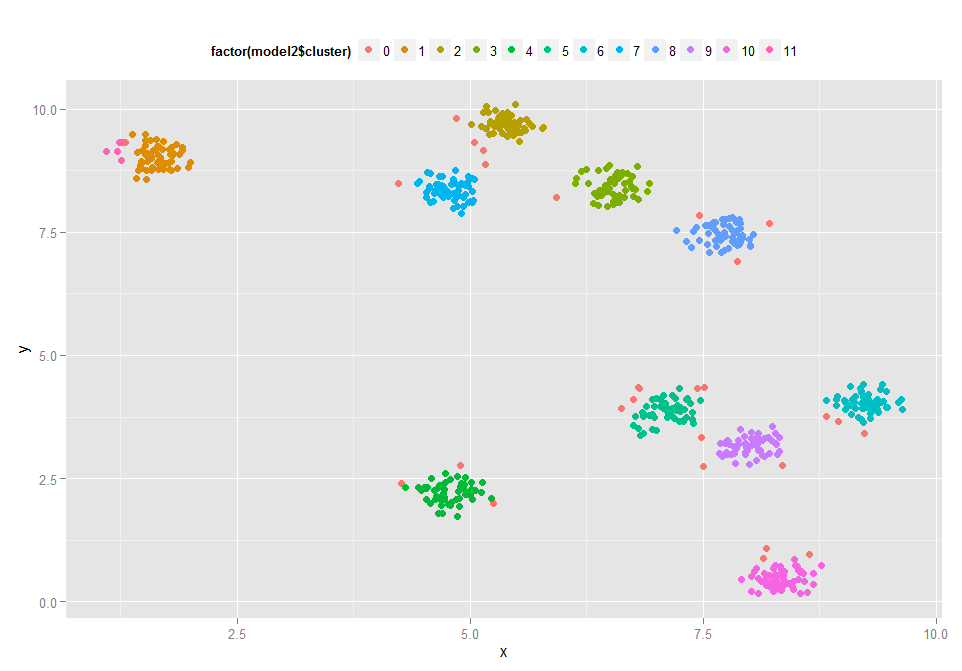www.cnblogs.comDBSCAN输出结果

1 dbscan是基于密度计算聚类的，会剔除异常（噪声点）。如上图中的类别0，就是dbscan算法聚类出的噪声点（不是核心点且不再核心点的邻域内）。

2 k-means需要指定k值，并且初始聚类中心对聚类结果影响很大。

3 k-means把任何点都归到了某一个类，对异常点比较敏感。

 

 

其它的观点。来自《数据挖掘导论》[美]Pang-Ning Tan,Michael Steinbach,Vipin Kumar 著 page355-356

为了简化比较，我们假定对于K均值和DBSCAN都没有距离的限制，并且DBSCAN总是将与若干个核心点相关联的边界点指派到最近的核心点。

1. K均值和DBSCAN都是将每个对象指派到单个簇的划分聚类算法，但是K均值一般聚类所有对象，而DBSCAN丢弃被它识别为噪声的对象。

2. K均值使用簇的基于原型的概念，而DBSCAN使用基于密度的概念。

3. K均值很难处理非球形的簇和不同大小的簇。DBSCAN可以处理不同大小或形状的簇，并且不太受噪声和离群点的影响。当簇具有很不相同的密度时，两种算法的性能都很差。

4. K均值只能用于具有明确定义的质心（比如均值或中位数）的数据。DBSCAN要求密度定义（基于传统的欧几里得密度概念）对于数据是有意义的。

5. K均值可以用于稀疏的高维数据，如文档数据。DBSCAN通常在这类数据上的性能很差，因为对于高维数据，传统的欧几里得密度定义不能很好处理它们。

6. K均值和DBSCAN的最初版本都是针对欧几里得数据设计的，但是它们都被扩展，以便处理其他类型的数据。

7. 基本K均值算法等价于一种统计聚类方法（混合模型），假定所有的簇都来自球形高斯分布，具有不同的均值，但具有相同的协方差矩阵。DBSCAN不对数据的分布做任何假定。

8. K均值DBSCAN和都寻找使用所有属性的簇，即它们都不寻找可能只涉及某个属性子集的簇。

9. K均值可以发现不是明显分离的簇，即便簇有重叠也可以发现，但是DBSCAN会合并有重叠的簇。

10. K均值算法的时间复杂度是O(m)，而DBSCAN的时间复杂度是O(m^2)，除非用于诸如低维欧几里得数据这样的特殊情况。

11. DBSCAN多次运行产生相同的结果，而K均值通常使用随机初始化质心，不会产生相同的结果。

12. DBSCAN自动地确定簇个数，对于K均值，簇个数需要作为参数指定。然而，DBSCAN必须指定另外两个参数：Eps（邻域半径）和MinPts（最少点数）。

13. K均值聚类可以看作优化问题，即最小化每个点到最近质心的误差平方和，并且可以看作一种统计聚类（混合模型）的特例。DBSCAN不基于任何形式化模型。

 

所以，不同的数据集和场景，需要运用不同的聚类算法。

3.数据粒度的性质

数据仓库是一种资讯系统的资料储存理论，此理论强调利用某些特殊资料储存方式，让所包含的资料，特别有利于分析处理，以产生有价值的资讯并依此作决策。
利用数据仓库方式所存放的资料，具有一旦存入，便不随时间而更动的特性，同时存入的资料必定包含时间属性，通常一个数据仓库皆会含有大量的历史性资料，并利用特定分析方式，自其中发掘出特定资讯。

数据仓库的特性

主题导向（Subject-Oriented）
有别于一般OLTP系统，数据仓库的资料模型设计，着重将资料按其意义归类至相同的主题区（subject area），因此称为主题导向。举例如Party、Arrangement、Event、Product等。
集成性（Integrated）
资料来自企业各OLTP系统，在数据仓库中是集成过且一致的。
时间差异性（Time-Variant）
资料的变动，在数据仓库中是能够被纪录以及追踪变化的，有助于能反映出能随着时间变化的资料轨迹。
不变动性（Nonvolatile）
资料一旦确认写入后是不会被取代或删除的，即使资料是错误的亦同。（i.e.错误的后续修正，便可因上述时间差异性的特性而被追踪）

 

粒度问题是设计数据仓库的一个最重要方面。粒度是指数据仓库的数据单位中保存数据的细化或综合程度的级别。细化程度越高，粒度级就越小；相反，细化程度越低，粒度级就越大。确定粒度是数据仓库开发者需要面对的一个重要的设计问题。如果数据仓库的粒度确定合理，设计和实现中的其余方面就可以非常顺畅地进行；反之，如果粒度确定的不合理就会是其他所有方面都很难进行。粒度对于数据仓库体系结构设计人员来说，非常重要，因为粒度会影响到那些依赖于从中获取数据的数据仓库的所有环境。
粒度的主要问题是使其处于一个合适的级别，粒度的级别既不能太高也不能太低。低的粒度级别能提供详尽的数据，但要占用较多的存储空间和需要较长的查询时间。高的粒度级别能快速方便的进行查询，但不能提供过细的数据。在选择合适粒度级别的过程中，要结合业务的特点，分析的类型、依据的总的存储空间的等因素综合考虑。

4.召回率 准确率

5.在多元线性回归模型中，若某个解释变量对其余解释变量的判定系数接近1，则表明模型中存在（C）？

A．异方差

B．自相关

C．多重共线性

D．设定误差

6.LR中的R2是什么？

统计学--线性回归决定系数R2 - CSDN博客​blog.csdn.net

决定系数（coefficient ofdetermination），有的教材上翻译为判定系数，也称为拟合优度。
决定系数反应了y的波动有多少百分比能被x的波动所描述，即表征依变数Y的变异中有多少百分比,可由控制的自变数X来解释.
表达式：R2=SSR/SST=1-SSE/SST
其中：SST=SSR+SSE，SST(total sum of squares)为总平方和，SSR(regression sum of squares)为回归平方和，SSE(error sum of squares) 为残差平方和。

R2越大，说明x对y的解释程度越高。

 

如果你有k个解释变量，但是只有k个样本，会发生什么情况？完全拟合，R2=1.

这样随着样本容量的增加，R2肯定是先减少的，因为一旦你有k+1个样本，R2<1.

但是随着样本继续增大，R2会最终收敛到一个确定的值，即1减去误差项方差除以y的方差。

 

 

7.X={1,2,3}可产生___个关联规则？C

A . 4
B . 5
C . 6
D . 7

 

8,.有关数据仓库的开发特点

数据仓库的设计与开发

9.

下列不是SVM核函数的是： B

• A 多项式核函数
• B logistic核函数
• C 径向基核函数
• D Sigmoid核函数

 

链接：https://www.nowcoder.com/questionTerminal/732300dcca8d49bca7183c5dc28d3236
来源：牛客网
选B;
支持向量机是建立在统计学习理论基础之上的新一代机器学习算法，支持向量机的优势主要体现在解决线性不可分问题，它通过引入核函数，巧妙地解决了在高维空间中的内积运算，从而很好地解决了非线性分类问题。
构造出一个具有良好性能的SVM，核函数的选择是关键．核函数的选择包括两部分工作：一是核函数类型的选择，二是确定核函数类型后相关参数的选择．因此如何根据具体的数据选择恰当的核函数是SVM应用领域遇到的一个重大难题，也成为科研工作者所关注的焦点，即便如此，却依然没有得到具体的理论或方法来指导核函数的选取．
1、经常使用的核函数
核函数的定义并不困难，根据泛函的有关理论，只要一种函数 K ( x i , x j ) 满足Mercer条件，它就对应某一变换空间的内积．对于判断哪些函数是核函数到目前为止也取得了重要的突破，得到Mercer定理和以下常用的核函数类型：
(1)线性核函数
K ( x , x i ) = x ⋅ x i
(2)多项式核
K ( x , x i ) = ( ( x ⋅ x i ) + 1 ) d
(3)径向基核（RBF）
K ( x , x i ) = exp ( − ∥ x − x i ∥ 2 σ 2 )
Gauss径向基函数则是局部性强的核函数，其外推能力随着参数 σ 的增大而减弱。多项式形式的核函数具有良好的全局性质。局部性较差。
(4)傅里叶核
K ( x , x i ) = 1 − q 2 2 ( 1 − 2 q cos ( x − x i ) + q 2 )
(5)样条核
K ( x , x i ) = B 2 n + 1 ( x − x i )
(6)Sigmoid核函数
K ( x , x i ) = tanh ( κ ( x , x i ) − δ )
采用Sigmoid函数作为核函数时，支持向量机实现的就是一种多层感知器神经网络，应用SVM方法，隐含层节点数目(它确定神经网络的结构)、隐含层节点对输入节点的权值都是在设计(训练)的过程中自动确定的。而且支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值，也保证了它对于未知样本的良好泛化能力而不会出现过学习现象。
2、核函数的选择
在选取核函数解决实际问题时，通常采用的方法有：一是利用专家的先验知识预先选定核函数；二是采用Cross-Validation方法，即在进行核函数选取时，分别试用不同的核函数，归纳误差最小的核函数就是最好的核函数．如针对傅立叶核、RBF核，结合信号处理问题中的函数回归问题，通过仿真实验，对比分析了在相同数据条件下，采用傅立叶核的SVM要比采用RBF核的SVM误差小很多．三是采用由Smits等人提出的混合核函数方法，该方法较之前两者是目前选取核函数的主流方法，也是关于如何构造核函数的又一开创性的工作．将不同的核函数结合起来后会有更好的特性，这是混合核函数方法的基本思想．

10.什么办法可以减少过拟合

防止过拟合的几种方法

在机器学习和深度学习中，过拟合是一个十分常见的问题，一旦模型过拟合了，可能这个模型就无法适用于业务场景中了。所以为了降低产生过拟合的风险，机器学习中的大牛们提出了以下几种方法供大家使用：
引入正则化
Dropout
提前终止训练
增加样本量

 

多选题

1.数据清理中处理缺失值的办法？

链接：https://www.nowcoder.com/questionTerminal/c2d44d84529d426783e9631f92cbaad5?orderByHotValue=1&mutiTagIds=632&page=1&onlyReference=false
来源：牛客网
数据清理中，处理缺失值的方法有两种：
删除法：1）删除观察样本
2）删除变量：当某个变量缺失值较多且对研究目标影响不大时，可以将整个变量整体删除
3）使用完整原始数据分析：当数据存在较多缺失而其原始数据完整时，可以使用原始数据替代现有数据进行分析
4）改变权重：当删除缺失数据会改变数据结构时，通过对完整数据按照不同的权重进行加权，可以降低删除缺失数据带来的偏差
查补法：均值插补、回归插补、抽样填补等
成对删除与改变权重为一类
估算与查补法为一类

3.评价分类模型的尺度？

衡量分类器的性能指标 - CSDN博客

衡量分类器的性能指标

error rate: 这个不讲了， 当然是错误率越低越好。

不过值得提到的就是可以通过一个被称为confusion matrix的办法直观展示classification error。 继而可以引出三个指标。

准确率召回率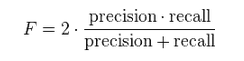F-measure

另一个衡量一个分类器的tool就是画出分类器的ROC曲线。 ROC 针对的是二元分类器。

ROC的横纵坐标分别是TPR(True positive rate), FPR(false positive rate)。

其中， TPR定义如下：

 

 

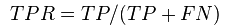
表示所有实际为是positve的样本被正确的判断为potive的样本数目比例。

FPR的定义如下：

 

 

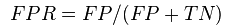
表示在所有实际为negative的样本中， 被错误的分为postive的比例。

给定一个二元分类器模型， 和这个分类器的阈值， 我们从分类后的结果中就可以得到一个x = FPR, y = TPR的值。

从（0， 0）到（1， 1）这条对角线将空间分成两部分， 左上和右下区域。 在这条线的左上部分代表着一个号的分类结果（胜过随机分类）， 右下的区域代表好于随机猜测了：

 

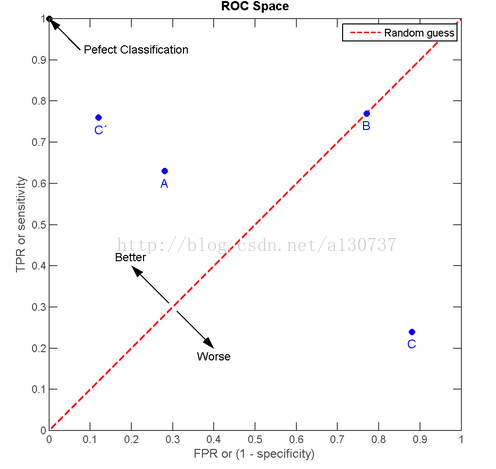
完美分类位于（1， 0）, 表示true positive 为1， false postive 为0。 上图的虚对角线是随机猜测得到的结果。 又叫做无识别率曲线。

为了画出ROC曲线， 我们需要阈值。 何为阈值？ 阈值就是判断一个样本是否为postive或者negative的numeric score。 Naiive Bayes给你的阈值是一个概率。 logistic regression也是一个可以看成概率的值。 Adaboost和SVM首先计算出一个numeric value, 然后作为一个sign的输入，对于这两个分类器， 那个numeric value也是一个score。 我们每一个样本都可以计算出这样的一个numeric value， 我们通过把这些nemeric value从小到大进行排序， 然后开始从最小的值开始， 不断设置阈值， 从下到上。 一直进行下去， 高于阈值的预测为positive， 低于阈值的预测为negative. 每个样本的score对应的就是这个样本的prediction strength。

4.影响K均值的主要因素？（与样本数有没有关？

K-means聚类结果的主要影响因素如下：
（1）距离测度选择。K-means聚类是以距离测度作为聚类依据，因此对于同一个样本点，选取不同的距离测度，得到的距离也不同，K-means聚类常用的距离测度为欧氏距离。

（2）数据特征。由于样本点本身属性具有的数据特征，在做聚类时，会因为数据影响距离，最终影响聚类效果，比如 xx 的有四个属性，其属性的数据范围为： x∈((0,1),(1,10),(1,100),(100,200))x∈((0,1),(1,10),(1,100),(100,200))，这种情况下，如果采取欧式距离测度，在计算时属性3和属性4的值对于距离的结果影响很大，可能直接影响了聚类结果。

处理方法：这种情况下可以进行数据预处理，对数据进行标准化，如0/1标准化、最小最大标准化。

（3）k值选取。k值的选取在K-means算法中是一个很常见又很重要的问题，选取好的k值，可以直接得到想要的聚类效果，如果k值选不好，可能会影响最终聚类效果。

处理方法：常见的选取k值的方法有以下两种：一是先把样本点plot出样本散点图观察数据特征，自己确定k值。二是设置一个循环，如 k∈[2,20]k∈[2,20] ，之后执行循环，找到聚类效果最好的情况对应的k值。

（4）初始中心点选取。由于样本聚簇初始中心点是随机选取的，具有不稳定性，如果随机选取的初始点距离较近，则很可能增加迭代次数、影响最终的聚类结果。

处理方法：在选取初始点时，对选取原则加以限制，如随机选取相互间距离较远的k个点作为初始聚簇中心点，这就是K-means++的基本原则。

 

 

5.小波分析怎么降维？

特征降维方法包括：Lasso，PCA，小波分析，LDA，奇异值分解SVD，拉普拉斯特征映射，SparseAutoEncoder，局部线性嵌入LLE，等距映射Isomap。

1. LASSO通过参数缩减达到降维的目的。

LASSO(Least absolute shrinkage and selection operator, Tibshirani(1996))
该方法是一种压缩估计，通过构造一个罚函数得到一个较为精炼的模型，使得压缩一些系数，同时设定一些系数为零。因此保留了子集收缩的优点，，是一种处理具有复共线性数据的有偏估计。Lasso 的基本思想是在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，从而能够产生某些严格等于 0 的回归系数，得到可以解释的模型。

2. 主成分分析PCA

PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。
设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X
2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值
3）求出协方差矩阵 
4）求出协方差矩阵的特征值及对应的特征向量
5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P
6）Y=PX即为降维到k维后的数据

PCA降维过程请参考http://www.cnblogs.com/zhangchaoyang/articles/2222048.html

3. 小波分析

小波分析有一些变换的操作降低其他干扰可以看做是降维。 http://www.360doc.com/content/15/0613/14/21899328_477836495.shtml

4. 线性判别LDA

线性判别式分析（Linear Discriminant Analysis），简称为LDA。也称为Fisher线性判别（Fisher Linear Discriminant，FLD），是模式识别的经典算法，在1996年由Belhumeur引入模式识别和人工智能领域。

基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

LDA与前面介绍过的PCA都是常用的降维技术。PCA主要是从特征的协方差角度，去找到比较好的投影方式。LDA更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更大，同一类别的数据点更紧凑。

详细请参考http://www.cnblogs.com/zhangchaoyang/articles/2644095.html

5. 拉普拉斯映射

拉普拉斯特征映射将处于流形上的数据，在尽量保留原数据间相似度的情况下，映射到低维下表示。

 

 

求解广义特征向量，取前几个非零最小特值对应的特向，即为原数据在低维下的表示。
资料来源于：http://blog.csdn.net/yujianmin1990/article/details/48420483

 

线性判别法？

机器学习中的数学(4)-线性判别分析（LDA）, 主成分分析(PCA)

LASSO可以减少参数？

在统计学和机器学习中，Lasso算法（英语：least absolute shrinkage and selection operator，又译最小绝对值收敛和选择算子、套索算法）是一种同时进行特征选择和正则化（数学）的回归分析方法，旨在增强统计模型的预测准确性和可解释性，最初由斯坦福大学统计学教授Robert Tibshirani于1996年基于Leo Breiman的非负参数推断(Nonnegative Garrote, NNG)提出[1][2]。Lasso算法最初用于计算最小二乘法模型，这个简单的算法揭示了很多估计量的重要性质，如估计量与岭回归（Ridge regression，也叫Tikhonov regularization）和最佳子集选择的关系，Lasso系数估计值(estimate)和软阈值（soft thresholding）之间的联系。它也揭示了当协变量共线时，Lasso系数估计值不一定唯一（类似标准线性回归）。
虽然最早是为应用最小二乘法而定义的算法，lasso正则化可以简单直接地拓展应用于许多统计学模型上，包括广义线性模型，广义估计方程，成比例灾难模型和M-估计[3][4]。Lasso选择子集的能力依赖于限制条件的形式并且有多种表现形式，包括几何学，贝叶斯统计，和凸分析。

lasso回归：

lasso回归的特色就是在建立广义线型模型的时候，这里广义线型模型包含一维连续因变量、多维连续因变量、非负次数因变量、二元离散因变量、多元离散因变，除此之外，无论因变量是连续的还是离散的，lasso都能处理，总的来说，lasso对于数据的要求是极其低的，所以应用程度较广；除此之外，lasso还能够对变量进行筛选和对模型的复杂程度进行降低。这里的变量筛选是指不把所有的变量都放入模型中进行拟合，而是有选择的把变量放入模型从而得到更好的性能参数。 复杂度调整是指通过一系列参数控制模型的复杂度，从而避免过度拟合(Overfitting)。 对于线性模型来说，复杂度与模型的变量数有直接关系，变量数越多，模型复杂度就越高。 更多的变量在拟合时往往可以给出一个看似更好的模型，但是同时也面临过度拟合的危险。

 

lasso的复杂程度由λ来控制，λ越大对变量较多的线性模型的惩罚力度就越大，从而最终获得一个变量较少的模型。除此之外，另一个参数α来控制应对高相关性(highly correlated)数据时模型的性状。 LASSO回归α=1，Ridge回归α=0，这就对应了惩罚函数的形式和目的。我们可以通过尝试若干次不同值下的λ，来选取最优λ下的参数，还可以结合CV选择最优秀的模型。