自由群

• 前言
  • 本文内容
  • 声明
• 自由群
  • 引入
    • 经典命题逻辑
    • 自由群的引入
  • 定义
    • 泛性质
      • 泛性质的意义
    • 构造
      • 字符
      • 字(word)
      • 规约
      • (自由)群结构
    • 证明
      • 形式化
      • diamond property
      • 泛性质
• 自由群与“生成”
  • 生成子群
  • 展示
• 草草结尾

前言

果然，坚持写博客是一件非常困难的事。按照计划，这篇博客一年前就该写出来了，那个时候我还在坚持学抽象代数——结果中间不知道发生了什么
总而言之一直耽搁到现在。

本文内容

本文内容有：

1. 自由群的引入和定义
2. 自由群的构造
3. 自由群的部分性质及证明。

没有：

1. 更高级的观点
2. 与其它知识点的链接

声明

我假定读者是一年前的自己，也就是学过一点群论，但是对概念懵懵懂懂。能看得懂证明，但看不懂命题。

希望这篇文章能给各位看官一点消遣（如果最后能写完的话）。

自由群

自由群是一种特殊的代数结构

引入

在代数里面我们常常会想要用一些已有的组件去生成一个代数结构，时髦一点说是求一个闭包。一个经典的例子是各种归纳构造：

经典命题逻辑

假设我们有一个命题变量的集合\(V=\{p,q,r,s,t,...\}\)，以及命题链接词的集合\(C=\{\rightarrow,\neg \}\)，我们归纳地定义命题集合\(P\)为

1. 对于任何\(p \in V\)，\(p\)是一个命题。
2. 对于任何两个命题\(\varphi ,\psi\)，(\(\varphi \rightarrow \psi;)\)也是一个命题。
3. 对于任何命题\(\varphi\)，\(\neg\varphi\)也是一个命题。

按照对应的规则，我们有一些例子

1. \(p, q, r, s, t, ...\)
2. \(p \rightarrow q, (p \rightarrow q) \rightarrow r,...\)
3. \(\neg p, \neg (p \rightarrow q)\)

你应该相当熟悉这样的定义。它有很多种看待的方法，我们这里只用最简单的观点（也许吧）。基本的命题变量相当于我们的基础组件，而规则2，3则是两种操作 ： \(\neg\)代表一个单目操作，给它一个组件，返回一个（新的）组件；\(\rightarrow\)代表一个二元操作，给它两个组件，返回一个（新的）组件。而我们最终得到的结构是从基础组件出发所有有限步操作构成的闭包。（一般的逻辑学教材会在这里证明，归纳定义的结果是所有有限构造的命题。）

这种定义的好处在哪里呢？当我们拿到一个命题时，我们同时知道了它是如何被构造出来的。只要知道

1. 如何解释每个变量
2. 如何解释连接符的真值

我们就可以直接导出整个命题的真值。

	命题变量	蕴含	取反
P	\(\{p,q,..,\}\)	\(\varphi, \psi \Rightarrow \phi \rightarrow \psi\)	\(\phi \Rightarrow \neg \phi\)
\(\{0,1\}\)	\(\mathbb{Z}/2\mathbb{Z}\)	\(m,n \Rightarrow (m \times (n + 1) + 1) mod 2\)	\(m \Rightarrow (m + 1) mod 2\)

这里，只要我们有一个从命题变量到真值的映射\(f:V \rightarrow\mathbb{Z}/2\mathbb{Z}\)，给我们一个命题我们就能知道命题的真值。

比如，假设我们有\(\{ p \mapsto 0, q \mapsto 1, r \mapsto 0\}\)，那么对于命题\(p \rightarrow q\)，我们知道这里是\(p\)和\(q\)的值进行一次蕴含操作，那么命题的真值就是\((0+1) mod 2 = 1\)而\((p \rightarrow q) \rightarrow r\)则是1再和\(r\)的值\(0\)做一次蕴含操作，结果是\((1 \times (0 + 1) + 1) mod 2 = 0\)。

如果我们把1解释为真而把0解释为假，我们就证明了两个命题的真值。当然这里我们省略了很多工作：比如操作的良定义性，命题的唯一可读性等等。不过你应该能大概领会到这种导出的意义：对于任何一个有相同signature(也就是有一个一元操作和一个二元操作)的代数结构\(N\)，我们只需要把每个基础组件解释成\(N\)的元素，那么这个解释就会自动扩展成对整个自由代数的解释\(V\)：

1. 每个\(P\)中的元素都解释成\(N\)的一个元素，即\(\forall p \in P, p \in dom(V)\)
2. 这种解释是保留操作的（即一个同态)，比如，\(V(A \rightarrow B)\)一定会解释成\((V(A) \times (V(B) + 1) +1) mod 2\)
3. 这种扩展是唯一的，比如每个命题只有一个真值。

从这个例子中我们大概可以猜测 自由 的意义。

事实上这种定义可以用一个交换图来表示。

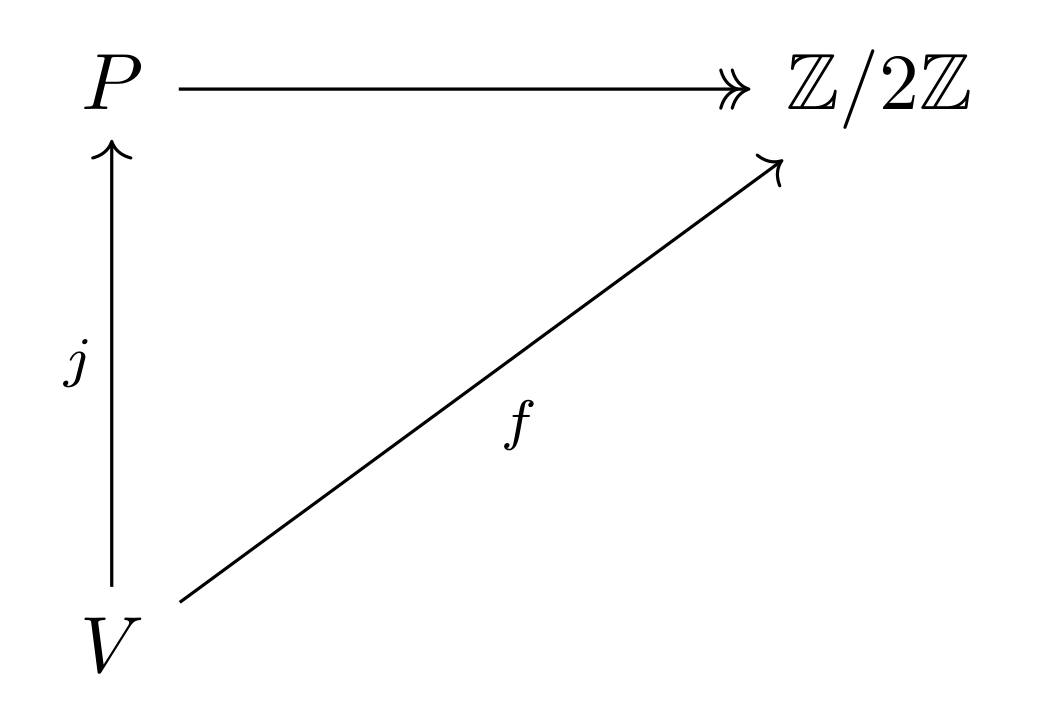
（如果你能忍受一些陌生的词语），我们把命题定义为了一个自由代数。只不过我们这里没有证明导出的函数\(P \rightarrow \mathbb{Z}/2\mathbb{Z}\)是良定义的（并且唯一）的。

在这里我们总结一下：

1. 这是一种对基础组件和操作的解释
2. 每个元素都是 有限步 内构造完成的
3. 每个操作满足单射与正交
   1. 若\(\varphi \rightarrow \psi=\varphi' \rightarrow \psi'\), 则\(\varphi = \varphi'\)且\(\psi = \psi'\)
   2. 若\(\neg\varphi=\neg\psi\)，则\(\varphi=\psi\)
   3. \(\varphi \rightarrow \psi \not= \neg \chi\)

这很重要。

自由群的引入

接下来我们要谈谈自由群。同样的，我们有一些基础组件，想要构造一个群。
稍微形式一点，我们有一个集合\(A\)，想要在A的基础上构造一个足够一般的群\(F(A)\)，首先它要是一个群，其次需要编码基础组件的所有有限次操作。

与命题逻辑不同的是，群里面有三种操作（命题逻辑有两种，蕴含和否定），分别是单位元\(e: G\), 求逆\(\iota: G \rightarrow G\)以及最重要的组合\(m: G \times G \rightarrow G\)。
注意到单位元是一个没有参数的操作，也就是一个常量。（简化，理解万岁）

接下来要做的就是照着命题逻辑画瓢，我们给几个经典的例子。

1. 空集

   假如\(A = \emptyset\)，\(F(A)\)应该是什么？当然不可能是\(A\)自己——群至少要有一个元素。

   1. 首先要有一个常量e，不妨假设叫nil。
   2. 因为基础组件是空集，所以跳过这一步
   3. 对于求逆，它一定满足nil的逆是nil
   4. 对于组合，nil和nil组合必定还是nil

   注意到3 和 4中没有提到\(F(A)\)中除nil之外的定义，因为我们看到：

   命题：\(F(\emptyset)\) 中只有nil

2. singleton

   假如\(a = \{ a\}\)，那么\(F(A)\)应该是什么？

   1. 首先要有一个常量nil
   2. 其次要有一个常量a
   3. 求逆\(\iota\)将\(a\)映射到\(\iota(a)\)
      1. 一定会有\(\iota(\iota(a)) = a\)
   4. 组合\(m\)将\(a,b\)映射到\(m(a,b)\)
      1. 一定会有\(m(a,\iota(a))=m(\iota(a),a)=nil\)

   如果我们把\(\iota(a)\)写成\(a^{-1}\)，把\(m(a,a)\)写成\(a^2\)，类似的定义
   \(m^z, z\in \mathbb{Z}\)。那么，\(F(\{ a\})\) 就是

   \[ \{..., a^{-2} , a^{-1}, nil , a^{1}, a^{2}, ...\} \]

   换言之，除了最基本的性质外，我们不对操作做任何要求。这也是自由群的另外一个说明: define a group from a set by the most efficient way 。

   （这里说个题外话，群有许多等价定义，在这里使用的是最简单的三个操作以及封闭语义。原因是操作越少，定义中的公理就越多，操作需要满足的性质就越多。）

定义

如果你看到这里的话，上文全是扯淡

这里我们用泛性质定义自由群，然后给出一个具体的构造及其证明。

泛性质

对于集合\(A\)，它的自由群是一个二元组\((j,F(A))\)，其中：

1. \(j\)是一个从\(A\)到\(F(A)\)的映射
2. \(F(A)\)是一个群，并且满足以下性质

对所有的群\(G\)以及映射\(k: A \rightarrow G\)，一定存在唯一一个 群同态 \(\varphi : F(A) \rightarrow G\)
使得

\[\forall a \in A, \varphi( j (a)) = k(a) \]

也就是图

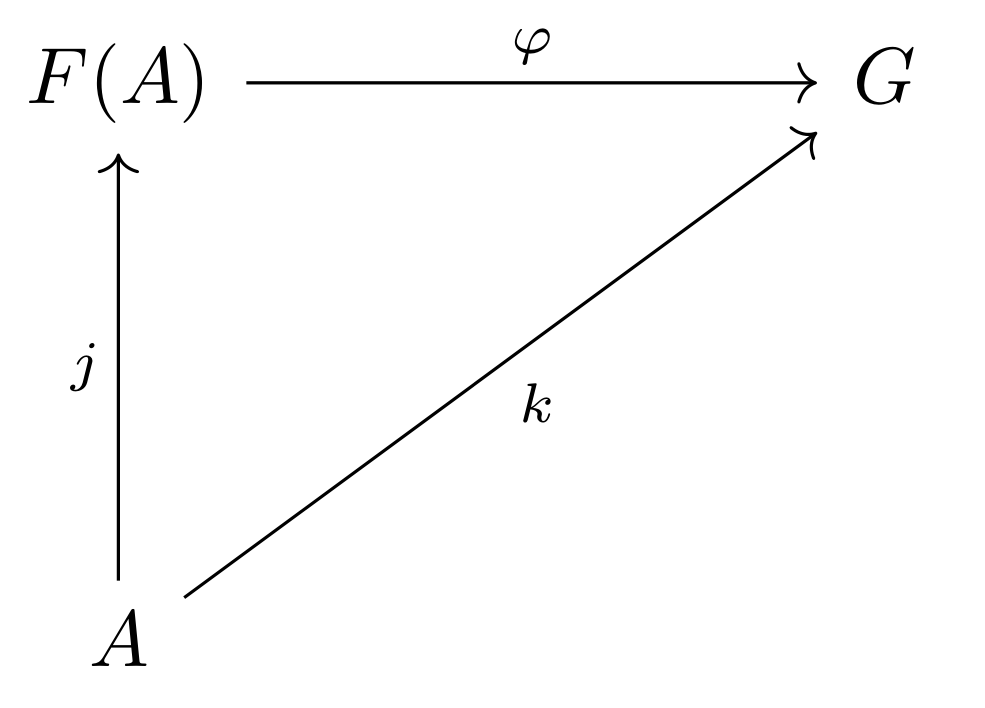
满足交换性。

泛性质的意义

直观上，泛性质的意义满足我们上面的刻画。（如果你不认为这是循环定义的话）

1. 注意到\(k: A \rightarrow G\)是一个任选的映射，“我们把基础组件任意地解释成某个群\(G\)中的元素”
2. 泛性质保证存在一个同态，“那么自由代数中的元素自动地解释成\(G\)的元素，并且保留操作”
3. 同态是唯一的，“这种解释是唯一的”

构造

容易验证，上面给出的\(F(\{ a\})\)满足这个性质。现在我们需要一个更一般的构造过程。

字符

我们假定存在一个字符的集合\(\mathcal{A}\)，满足要求：

1. 对于任意\(a \in A\)，都有\(a, a^{-1} \in \mathcal{A}\)
2. 1 中引入的字符各不相同

字符是一个比较糟糕的概念，注意到\(\mathcal{A}\)中引入的\(a\)与\(A\)中的\(a\)是不同的。这里的逆也仅仅是一种标记，因为我们还没有定义操作。
我们可以把它想象成C里的char，lisp里的symbol等等……

不过我个人比较喜欢这样的定义：
令\(\mathcal{A} \subseteq （\mathbb{N} \times A\)是满足如下定义的最小集合

1. 对于任意\(a \in A\)，都有\((a,0),(a,1)\in \mathcal{A}\) (\(a, a^{-1}\))
   这样自动保证了字符各不相同。

总之我们只是需要一些各不相同的字符而已

字(word)

令字的集合\(W\)为满足以下条件的最小集合：

1. 一个特殊空字符\(() \in W\) 满足\(()\)与\(\mathcal{A}\)中所有的元素各不相同
2. \(\mathcal{A}\) 上的有限长序列都在\(W\)中

（按照上面的第二种定义可以直接把\(()\)定义成自然数0）

例如，对于\(A = {x,y}\)，我们有一些这样的字：

1. \(()\)
2. \(xx^{-1}xyyy^{-1}xyxy\)
3. ...

自然，每个字都是有限长。

规约

（首先还是一段废话）
我们不能直接在字上定义群操作，一种想法是

1. \(m(w_1,w_2)=~~w_1 ++ w_2~~\)
2. \(e = ()\)
3. 求逆时直接将字逆转并把每个字符的正负都调转。

其中\(++\)是简单的序列拼接操作，特殊字符\(()\)是拼接的单位元。

但是，我们需要\(m(x,x^{-1})=()\)而不是\(m(x,x^{-1})=xx^{-1}\)。所以我们需要在最简形式的字上面定义群。换言之，不能存在\(xx^{-1}\)或者\(x^{-1}x\)这样的子序列。

我们定义一次规约操作\(R:W \rightarrow W\)为消去参数最左边的可消子式，如果没有子式可以消则保持不变，全部消完则替换成空字符。比如：

1. \(R(x)=x\)
2. \(R(xy)=xy\)
3. \(R(xx^{-1}=()\)
4. \(R(xx^{-1}yy^{-1})=yy^{-1}\)
5. \(R(xx^{-1}xyyy^{-1}xyxy)=xyyy^{-1}xyxy\)

注意到一次规约前后字的长度至多减2。因此对于长\(n\)的序列\(w\)，我们定义规约\(R':W \rightarrow W\)为

\[R'(w) := R^{\lfloor \frac{n}{2} \rfloor}(w) \]

显然\(R'(w)\)必然是最简形式。

(自由)群结构

接下来我们就可以在最简形式的字的集合上构造群\(F(A)\)了，也就是定义三个操作。

集合\(F(A)\)为最简形式的字构成的集合，操作定义为：

1. \(m(w_1,w_2) := R'(w_1 ++ w_2 )\)
2. \(e := ()\)
3. 对于\(w=x_1x_2,..,x_n\), \(\iota(w) :=\iota(x_n),\iota(x_{n-1}),...,\iota(x_1)\)

其中\(\iota(x) := x^{-1}\)，\(\iota(x^{-1})=x\)。换言之，简简单单的\(m(xy^{-1},y)=x\)。

自由群的定义\(j,F(A)\)的另一部分是\(j:A \rightarrow F(A)\)，我们直接定义\(j(a)=a\)就好，注意到右边是字符\(a\)而不是\(A\)里面的\(a\)。

证明

我们还需要证明这个构造是对的。

1. 验证三个操作在\(F(A)\)上满足群论公理。
2. 验证满足泛性质

对于1我们只证明最难的部分，也就是\(m\)满足结合律。
为了证明\(m(w_1,m(w_2,w_3))=m(m(w_1,w_2),w_3)\)，我们需要证明

\[R'(w_1 ++ R'(w_2 + w_3)) = R'(R'(w_1 ++ w_2) ++ w_3) \]

我们cut一下，只需要（为什么？）证明对于任意字\(w\)，无论我们如何选择消去的顺序，最终的结果都是一样的。举几个例子

1. 对于\(xx^{-1}x\)，任意选择两个子式之一，结果都是\(x\)
2. 对于\(x^{-1}yy^{-1}xx^{-1}\)，最终的结果是\(x^{-1}\)

尽管看起来很简单，但证明并不trivial，如果你有兴趣可以先试试简单的归纳法。

形式化

首先形式化地定义消去与最简性质。注意到我们已经定义了\(()\)为\(++\)的单位元。

1. 消去关系\(R_1 \subseteq W \times W\)
   1. 对任何字符\(x\)，\((x \iota(x),()) \in R_1\)
2. 合拍关系\(R_2 \subseteq W \times W\)
   1. 对于\((a,()) \in R_1\), 以及任意\(w_1,w_2 \in W\)，均有\((w_1 ++ a ++ w_2,w_1 ++ w_2) \in R_2\)
3. 传递关系\(R_3 \subseteq W \times W\)
   1. 对任何\(w \in W\)，都有\((w,w) \in R_3\)
   2. 对任何\((a,b) \in R_2\)，都有\((a,b) \in R_3\)
   3. 若\((a,b) \in R_3,(b,c) \in R_3\)，则\((a,c) \in R_3\)
4. 范式。对于\(w \in W\)，如果有\(\forall w' \in W,(w,w') \in R_3 \Rightarrow w'=w\)，则称\(w\)为范式(normal form)
5. 字\(w\)的最简形式。\(w\)的最简形式是满足\((w,w') \in R_3\)的范式\(w'\)

\(R_1\)的定义是基础(basis)，\(R_2\)是一步消去，\(R_3\)是0步或多步消去。

容易证明，对任意字\(w\)，\(R'(w)\)都是它的一个最简形式（为什么？）。我们要证明的就是，每个字只有一个最简形式（或者是所有最简形式都相等）。

diamond property

一种方法是著名的钻石性质，命题长这个样子: 对任意字\(w\)，如果有\(w\)一步消去到\(w_1\)，\(w\)又能一步消去到\(w_2\)，那么一定存在一个字\(w_3\)，使得\(w_1\)和\(w_2\)都能0步或多步消去到\(w_3\)。它的图形揭示了它为什么叫“钻石”性质。

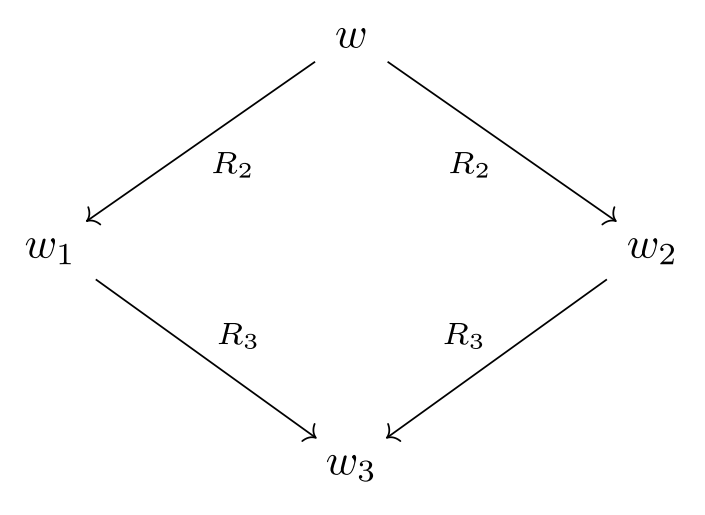
意识到这一性质之后证明就会变得简单。我们对\(w\)的长度进行归纳，假定所有长度小于\(w\)的字都只有一种范式，考虑\(w\)，我们证明\(w\)有diamond property。若\(w R_2 w_1\)，\(w R_2 w_2\)，
那么要么二者消去的地方相同，\(w_1 = w_2\)，此时命题立即成立，否则我们考虑\(w_1\)和\(w_2\)消去的“位置”

1. 二者不重叠，即\((...xx^{-1}...yy^{-1}...)\)，不妨设\(w_1=(...yy^{-1}...)\), \(w_2 = (...xx^{-1}...)\)，那么显然两者只需要消去剩下的那个子式就可以了。
2. 二者重叠，即\(...xx^{-1}x...\)，其中\(w_1\)选择消去\(...(xx^{-1})x...\)，\(w_2\)选择消去\(...x(x^{-1}x)...\)。注意到这种时候立即有\(w_1=w_2\)，成立

钻石性质告诉我们，\(w_1\),\(w_2\)的范式相同，都等于\(w_3\)的范式。因为它们的长度都小于\(w\)，根据归纳假设它们都只有一个范式，并且因为\(w_3\)的范式也是\(w_1(w_2)\)的范式，所以\(w_1\)和\(w_2\)的所有范式都等于\(w_3\)的那唯一一个范式。

推而广之，\(w\)的所有一步消去的范式都相同，因此\(w\)只有一个范式，归纳成立。
因此

\[R'(w_1 ++ R'(w_2 + w_3)) = R'(R'(w_1 ++ w_2) ++ w_3) \]

成立，操作\(m\)满足结合律。

泛性质

验证了\(F(A)\)是群结构之后，我们再验证它满足泛性质，这个证明非常简单。对于任意群\(G\)以及任意函数\(k:A \rightarrow G\)，我们现在来导出一个群同态出来。

我们定义函数\(\varphi : F(A) \rightarrow G\)为：

1. \(\forall a \in A, \varphi(j(a)) = k(a), \varphi(\iota(j(a)))=k(a)^{-1}\)
2. \(\varphi(()) = e_{G}\)
3. \(\forall w=(x_1,x_2,...,x_n)\in F(A),\varphi(w)=\varphi(x_1)*_{G}\varphi(x_2)...\varphi(x_n)\)

容易验证这是一个良定义，注意到定义3直接保证了\(\varphi\)是一个群同态，以及1保证了\(\varphi\circ j = k\)。

另外假设存在另一个满足要求的同态\(\psi\)，那么群同态要求强迫\(\psi\)也需要满足1,2,3，因此\(\varphi = \psi\)。
泛性质由此得证。

自由群与“生成”

自由群一个直接的应用是它可以用来方便地表达很多概念。我们这里只讨论关于生成的性质。

生成子群

对于群\(G\)，以及集合\(A\subseteq G\)，生成子群\(\langle A\rangle\)是A中的元素按照\(G\)的操作扩展成的群。比如我们都很熟悉的某个元素\(g \in G\)生成的群

\[\{..., g^{-2} , g^{-1}, e , g^{1}, g^{2}, ...\} \]

（有没有觉得眼熟？）一般来说它会定义成

\[\langle A\rangle = \bigcap_{A \subseteq H \leq G}{H} \]

也就是包含\(A\)的最小的集合。有了生成子群之后，我们只需要令\(k:A \rightarrow G = id\)，就可以直接导出一个群同态\(\varphi\)满足\(\varphi\circ j=k\)。于是可以定义

\[\langle A\rangle = img(\varphi) \]

不难验证这两种定义等价。
于是我们说群\(G=\langle A\rangle\)，当且仅当导出的同态是满射。

展示

使用自由群的好处在于，当我们有了同态，我们就有了商群。注意任何一个群\(G\)都有某个自由群到它的满射（比如\(F(G)\)），那么对于

\[\varphi : F(A) \twoheadrightarrow G \]

根据第一同构定理

\[G \cong \frac{F(A)}{ker(\varphi)} \]

换言之每个群都能表示成某个自由群的商群，这种表示方法称为群的展示(presentation)。

为方便，不需要完全地写出自由群的正规子群，只需要提供一些“关系”。我们把群的表示记作\(\langle A \mid R \rangle\)，意为群

\[\frac{F(A)}{N(R)} \]

其中\(R\)是\(F(A)\)的子集，\(N(R)\)是包含\(R\)的最小正规子群。由于\(() \in N(R)\), \(w \in R\)实际上表达了\(w \sim e\)。
比如\(R=\{x^2,y^3,xyxy\}\)就表示了\(x^2=e,y^3=e,yx=xy^{2}\)，于是\(\langle \{x,y\} \mid \{x^2,y^3,xyxy \} \rangle \cong S_3\)。

注意到正规子群的要求比子群要高。

草草结尾

虽然写之前就知道写的是没什么用的东西，但真写起来长度还是超出我的预计，所以不得不删减最后的应用部分。

就这样吧。