拉格朗日插值学习总结
简介
在数值分析中,拉格朗日插值法是以法国18世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。如果对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。上面这样的多项式就称为拉格朗日(插值)多项式。
题目大意
给出$n$个点,将过这$n$个点的最多$n-1$次的多项式记为$f$$\left(x\right)$,求$f$$\left(k\right)$的值。
拉格朗日插值法
一个最显然的思路就是直接高斯消元求出多项式的系数,但是这样做复杂度巨大$O\left(n^3\right)$且根据算法实现不同往往会存在精度问题。
而拉格朗日插值法可以在$O\left(n^2\right)$的复杂度内完美解决上述问题。
如图所示,将每一个点$\left(x_i,y_i\right)$在$x$轴上的投影$\left(x_i,0\right)$记为$H_i$。对于每一个$i$,我们选择一个点集$\{P_i\}\cup\{H_j|1\le i\le n,j\ne i\}$,作过这$n$个点的至多$n-1$次的线$g_i\left(x\right)$。图中$f\left(x\right)$用黑线表示,$g_i\left(x\right)$用彩色线表示。
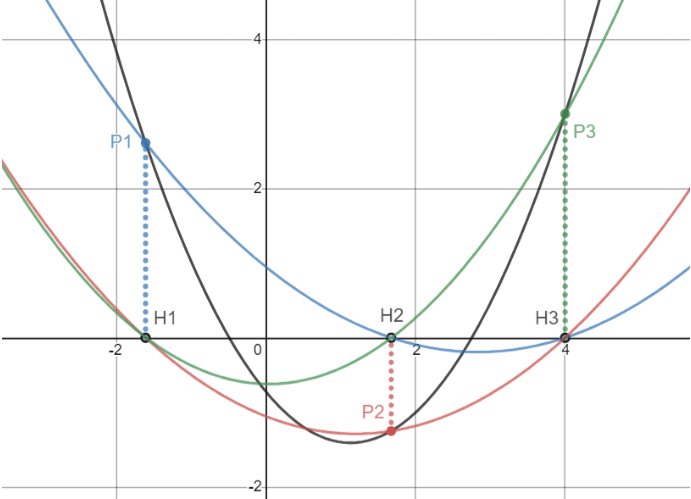
这样,我们得到了$n$个$g_i\left(x\right)\left(1\le i\le n\right)$,它们都在各自对应的$x_i$处的值$y_i$为,并且在其它$x_j\left(j\ne i\right)$处值为$0$。所以很容易构造出$g_i\left(x\right)$的表达式:
$$g_i\left(x\right)=y_i\prod\limits_{j\ne i}\frac{x-x_j}{x_i-x_j}$$
令$$\ell_i\left(x\right)=\prod\limits_{j\ne i}\frac{x-x_j}{x_i-x_j}$$
每个$\ell_i\left(x\right)$就是拉格朗日基本多项式(或称插值基函数)
拉格朗日基本多项式$\ell_i\left(x\right)$的特点是在$x_i$上取值为$1$,在其他的点$x_j,j\ne i$上取值为$0$。
最后,我们所求的$f\left(x\right)=\sum\limits_{i=1}^ng_i\left(x\right)$,即各$g\left(x\right)$之和。因为对于每一个$i$,都只有一条$g_i$经过$P_i$,其余$g_j$都经过$H_i$,故它们相加后在$x_i$的取值仍为$y_i$,即最后的和函数总是过所有$P_i$的。
公式整理即得拉格朗日插值法:
$$f\left(x\right)=\sum\limits_{i=1}^ny_i\prod\limits_{j\ne i}\frac{x-x_j}{x_i-x_j}$$
对于本题来说,只用求出$f\left(k\right)$的值,直接带入公式求即可。
复杂度:$O\left(n^2\right)$
Talk is cheap,show you code.
1 int n, k; 2 int a, b, ans; 3 int x[N ], y[N ]; 4 inline int ksm (int a, int b) 5 { 6 int res = 1; 7 while(b) 8 { 9 if(b & 1) res = res * a % P ; 10 a = a * a % P ; 11 b >>= 1; 12 } 13 return res; 14 } 15 inline int inv(int x) 16 { 17 return ksm (x, P - 2); 18 } 19 signed main() 20 { 21 read(n); read(k); 22 for(R int i = 1; i <= n; i++) read(x[i]), read(y[i]); 23 for(R int i = 1; i <= n; i++) 24 { 25 a = y[i] % P ; 26 b = 1; 27 for(R int j = 1; j <= n; j++) 28 { 29 if(i == j) continue; 30 a = a * (k - x[j]) % P ; 31 b = b * (x[i] - x[j]) % P ; 32 } 33 ans = (ans + a * inv(b) % P ) % P ; 34 } 35 writeln((ans + P ) % P ); 36 return 0; 37 }
(% P + P) % P 熟练得令人心疼(懂的都懂
优点与缺点
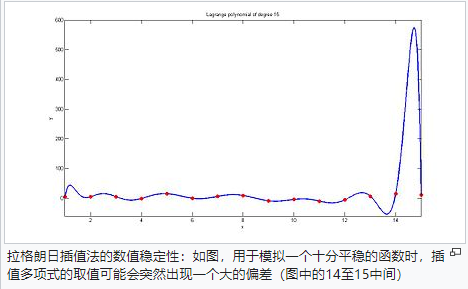
重心拉格朗日插值法
$$f\left(x\right)=\sum\limits_{i=1}^n y_i \prod\limits_{j\ne i}\frac{x-x_j}{x_i-x_j}$$
$$=\sum\limits_{i=1}^n y_i \frac{\prod\limits_{j\ne i}\left(x-x_j\right)}{\prod\limits_{j\ne i}\left(x_i-x_j\right)}$$
$$=\sum\limits_{i=1}^n y_i \frac{\prod\limits_{i=1}^n \left(x-x_i\right)}{\prod\limits_{j\ne i}\left(x_i-x_j\right)*\left(x-x_i\right)}$$
$$=\prod\limits_{i=1}^n \left(x-x_i\right)\sum\limits_{i=1}^n \frac{y_i}{\prod\limits_{j\ne i}\left(x_i-x_j\right)*\left(x-x_i\right)}$$
令$g=\prod\limits_{i=1}^n \left(x-x_i\right)$
令$w\left(i\right)=\prod\limits_{j\ne i} x_i-x_j$
那么柿子变成$$f\left(x\right)=g\sum\limits_{i=1}^n \frac{y_i}{\left(x-x_i\right)w\left(i\right)}$$
对于增加的插值点,我们只用$O\left(n\right)$更新所有的$w\left(i\right)$。
对于询问求值,我们先$O\left(n\right)$求出$g$,然后再$O\left(n\right)$套公式即可。
记得先预处理逆元。不然白送一个$log_2 n$
Talk is cheap,show you code.
1 int n, opt, x0, y0; 2 int x[N ], y[N ], w [N ], num ; 3 inline int ksm (int a, int b) 4 { 5 int res = 1; 6 while(b) 7 { 8 if(b & 1) res = res * a % P ; 9 a = a * a % P ; 10 b >>= 1; 11 } 12 return res; 13 } 14 inline int inv(int x) 15 { 16 return ksm (x, P - 2); 17 } 18 inline void insert(int x0, int y0) 19 { 20 num ++; 21 x[num ] = x0; 22 y[num ] = y0; 23 w [num] = 1; 24 for(R int i = 1; i <= num - 1; i++) 25 { 26 w [i] = w [i] * (x[i] - x0) % P ; 27 w [num ] = w [num ] * (x0 - x[i]) % P ; 28 } 29 } 30 inline int work(int x0) 31 { 32 int g = 1, ans = 0; 33 for(R int i = 1; i <= num ; i++) 34 { 35 if(x[i] == x0) return y[i]; 36 g = g * (x0 - x[i]) % P ; 37 } 38 for(R int i = 1; i <= num ; i++) 39 ans = (ans + y[i] * inv((x0 - x[i]) * w [i])) % P ;//我来白送 40 return (g * ans % P + P ) % P ; 41 } 42 signed main() 43 { 44 read(n); 45 for(R int i = 1; i <= n; i++) 46 { 47 read(opt); 48 if(opt == 1) 49 { 50 read(x0); read(y0); 51 x0 %= P ; y0 %= P ; 52 insert(x0, y0); 53 } 54 else 55 { 56 read(x0); 57 writeln(work(x0)); 58 } 59 } 60 return 0; 61 }

