20200724T1 【NOIP2015模拟10.28B组】序章-弗兰德的秘密

1|0Description

背景介绍
弗兰德，我不知道这个地方对我意味着什么。这里是一切开始的地方。3年前，还是个什么都没见过的少年，来到弗兰德的树下，走进了封闭的密室，扭动的封尘已久机关，在石板上知道了这个世界最角落的最阴暗的东西。那种事情，从未忘怀，从未动摇，我还记得，那一天，我，里修，第一次拔起了剑……

弗兰德的密室里，机关上方画着两棵树的字样，机关下方是一个有数字的刻度……
弗兰德最高的两棵树，只要知道两棵树的共同的相似度就行了……
给定两棵有根树，可以任意删除两棵树上的节点（删除一棵节点必须保证该节点的子树内的所有节点也必须要被删除，换一种说法，删除后的树必须联通并形成一棵树，且根节点不能被删除），使得删除后的两棵树同构，这两棵树有一个共同大小，即树的size，最大化同构的树的size即为机关的答案……

注：两棵同构的树要满足以下条件：
1、两棵树节点个数相等。
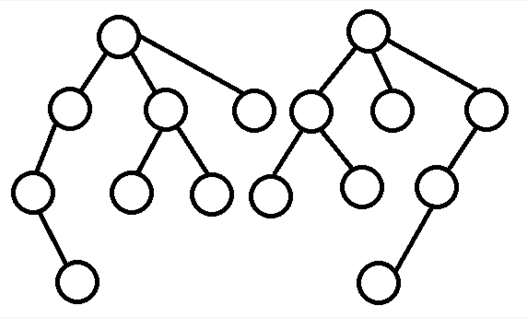
2、两棵树的以根节点的儿子为根子树对应同构。如下图，为两棵同构的有根树。
如下图，为两棵同构的有根树。

 

 一行两个整数n,m分别表示两棵有根树的大小。
以下n-1行描述第一棵树，每行两个数x,y表示x号节点是y号节点父亲。
以下m-1行描述第二棵树，每行两个数x,y表示x号节点是y号节点父亲。
数据保证两棵树的1号节点均为根。

 

一行一个数，表示两棵树的相似度（删除后最大化的同构树的大小）。

 

3 3
1 2
1 3
1 2
2 3

2
【样例解释】
第一棵树可以保留1号节点和2号节点删除3号节点，也可以保留1号节点与3号节点删除2号节点，
第二棵树保留1号节点和2号节点删除3号节点。
剩下的树同构，树的节点个数均为2。

2|0solution

一般没什么思路的就是DP了

f[x][y]表示第一棵树x节点与第二棵树y节点作为根节点时的最大同构

现在转移方程就很明显了

 

 

3|0code

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<queue>
 7 #include<vector>
 8 #include<stack>
 9 #include<set>
10 #include<deque>
11 #include<map>
12 using namespace std;

14 template <typename T> void read(T &x) {
    x = 0; int f = 1; char c;
    for (c = getchar(); c < '0' || c > '9'; c = getchar()) if (c == '-') f = -f;
    for (; c >= '0' && c <= '9'; c = getchar()) x = 10 * x + c - '0' ;
    x *= f;
}
template <typename T> void write(T x){
    if (x < 0) putchar('-'), x = -x;
    if (x > 9) write(x / 10);
    putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) { write(x); putchar('\n'); }
template <typename T> void writesn(T x) { write(x); putchar(' '); }

28 #define ll long long
29 #define inf 1234567890
30 #define next net
31 #define P 2147483647
32 #define N 1010
33 #define mid ((l+r)>>1)
34 #define lson (o<<1)
35 #define rson (o<<1|1)
36 #define R register
37 #define debug puts("zxt")
38 
39 int n, m , xx, yy;
int f[N ][N ], book[N ];
vector<int> ver1[N ], ver2[N ];
void dfs2(int x,int y)
{
    if(x >= ver1[xx].size())
    {
        f[xx][yy] = max(f[xx][yy], y);
        return;
    }
    dfs2(x + 1, y);
    for(R int i = 0; i < ver2[yy].size(); i++)
    {
        if(book[i]) continue;
        book[i] = 1;
        dfs2(x + 1, y + f[ver1[xx][x]][ver2[yy][i]]);
        book[i] = 0;
    }
}
void dfs1(int x)
{
    if(ver1[x].empty())
    {
        for(R int i = 1; i <= m ; i++) f[x][i] = 1;
        return;
    }
    for(R int i = 0; i < ver1[x].size(); i++) dfs1(ver1[x][i]);
    for(R int i = 1; i <= m ; i++)
    {
        if(!ver2[i].size()) f[x][i] = 1;
        else
70         {
            xx = x; yy = i;
            dfs2(0, 0);
            f[x][i]++;
        }
    }
}
signed main()
{
    //freopen("frand.in","r",stdin);
    //freopen("frand.out","w",stdout);
81     read(n); read(m );
    for(R int i = 1, x, y; i < n; i++)
    {
        read(x); read(y);
        ver1[x].push_back(y); 
    }
    for(R int i = 1, x, y; i < m ; i++)
    {
        read(x); read(y);
        ver2[x].push_back(y); 
    }
    dfs1(1);
    writeln(f[1][1]);
    return 0;
}

__EOF__

本文作者：是非成败转头空
本文链接：https://www.cnblogs.com/e-e-thinker/p/13374701.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！