最短路问题专题

一 Dijkstra算法

/*HDU2544
Input
每组数据第一行是两个整数N、M(N<=100，M<=10000)N表示成都的大街上有几个路口，
标号为1的路口是商店所在地，标号为N的路口是赛场所在地，M则表示在成都有几条路。
N=M=0表示输入结束。接下来M行，每行包括3个整数A，B，C（1<=A,B<=N,1<=C<=1000）,
表示在路口A与路口B之间有一条路，我们的工作人员需要C分钟的时间走过这条路。
Output
对于每组输入，输出一行，表示工作人员从商店走到赛场的最短时间
Sample Input
2 1
1 2 3
3 3
1 2 5
2 3 5
3 1 2
0 0
Sample Output
3
2
*/
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define INF 0x3f3f3f3;
int map[110][110],dis[110],visited[110];

void Dijkstra(int n,int x)
{
    int i,p,j,min;
    for (i=1; i<=n; i++)
    {
        dis[i]=map[1][i];
        visited[i]=0;
    }
    visited[x]=1;
    for (i=1; i<=n; i++)
    {
        min=INF;
        for (j=1; j<=n; j++)
        {
            if(!visited[j] && dis[j]<min)
            {
                p=j;
                min=dis[j];
            }
        }
        visited[p]=1;
        for (j=1; j<=n; j++)
        {
            if(!visited[j] && dis[p]+map[p][j]<dis[j])
            {
                dis[j]=dis[p]+map[p][j];
            }
        }
    }
}

int main()
{
    int n,m,i,j,a,b,t;
    while(scanf("%d%d",&n,&m),n+m)
    {
        for (i=1; i<=n; i++)
        {
            for (j=1; j<=n; j++)
            {
                map[i][j]=INF;
            }
        }
        for(i=1; i<=m; i++)
        {
            scanf("%d%d%d",&a,&b,&t);
            map[a][b]=map[b][a]=t;
        }
        Dijkstra(n,1);
        printf("%d\n",dis[n]);
    }
    return 0;
}

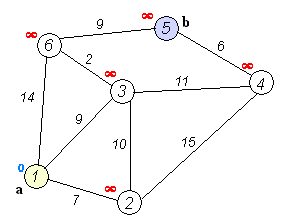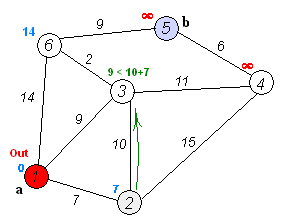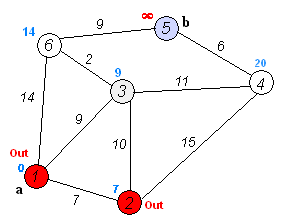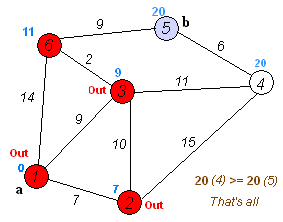
过程如图所示，求解单源最短路问题（固定起点），基于贪心算法

 

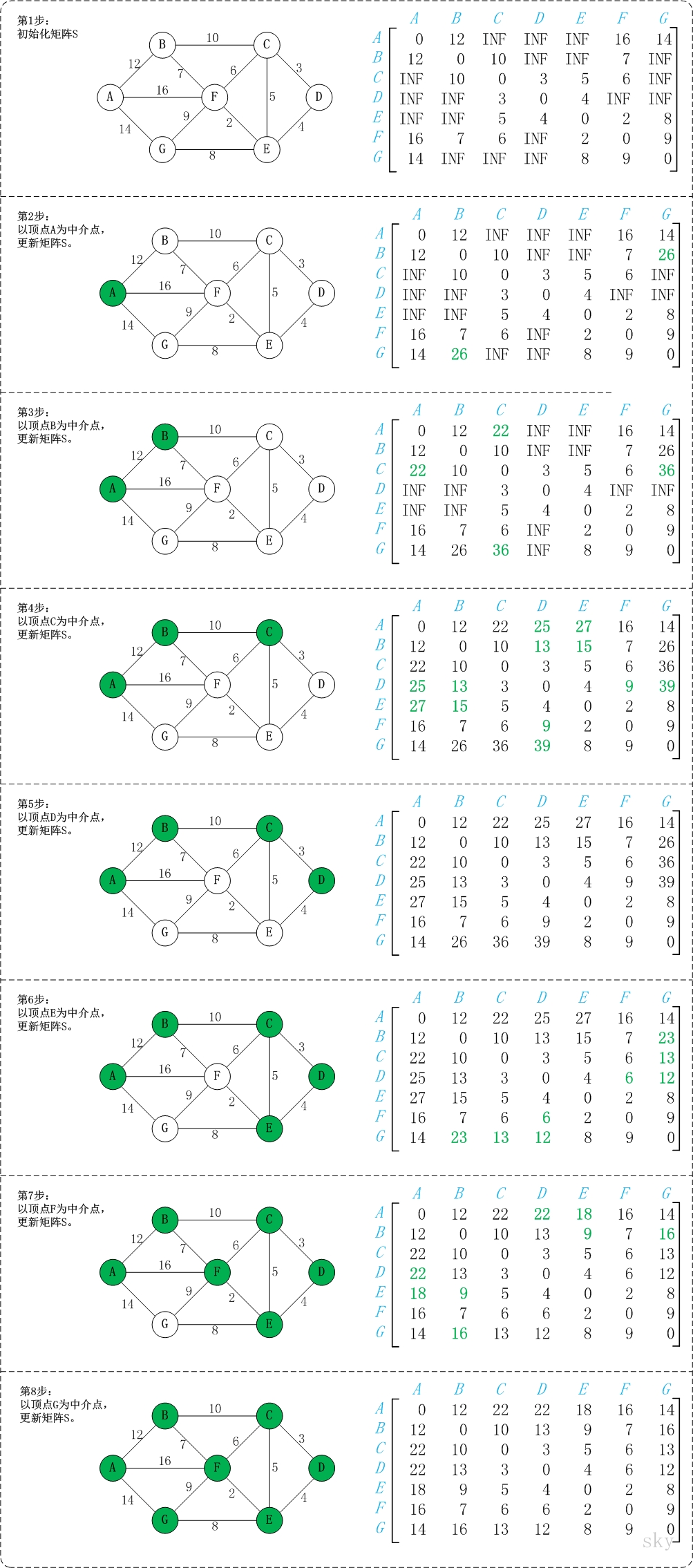
二 Floyd算法

#include <iostream>
#include <cstdio>
using namespace std;
const int INF=0x3f3f3f3f;
int dis[110][110];
int main()
{
    int i,j,k,n,m,p,q,s;
    while(scanf("%d%d",&n,&m),n+m)
    {
        for (i=1; i<=n; i++)
        {
            for(j=1; j<=n; j++)
            {
                dis[i][j]=INF;
            }
        }
        for (i=0; i<m; i++)
        {
            scanf("%d%d%d",&p,&q,&s);
            dis[p][q]=dis[q][p]=s;
        }
        for (k=1; k<=n; k++)
        {
            for (i=1; i<=n; i++)
            {
                for (j=1; j<=n; j++)
                {
                    if (dis[i][j]>dis[i][k]+dis[k][j])
                    {
                        dis[i][j]=dis[i][k]+dis[k][j];
                    }
                }
            }
        }
        printf("%d\n",dis[1][n]);
    }
    return 0;
}

Floyd算法是求任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，基于动态规划