快速排序

挖坑填数法+分治法（从别人的博客借鉴得到）

//快速排序   复杂度为O(nlogn)
void qucik_sort(int s[], int l, int r)
{
    //选定数组左边第一个数为基数
    //即在数组最左边先挖一个坑
    if(l < r)
    {
     int i = l;
     int j = r;
     int bnum = s[l];
     

     while( i < j)
     {
         while(s[j] >= bnum && i<j)   j--;    //从右向左找第一个小于bnum的数   
         /*思考：为什么需要i<j这个条件
           A:因为有可能在右指针向左移动时遇到 i==j 的情况，如果不跳出来，则s[i] = bnum这一步将出错
             毕竟循环终止的条件确切来说应该是 i==j 。*/

         if(i < j) s[i++] = s[j];             //将之前的坑填上，得到一个新的坑

         while(s[i] < bnum && i<j)   i++;     //从左向右找第一个大于等于bnum的数
         if(i < j) s[j--] = s[i]; 
     }

     s[i] = bnum;    //将最后遗留的坑填上基数

     qucik_sort(s,l,i-1);   //递归排序左半部分
     quick_sort(s,i,r);     //递归排序右半部分
    }

}

 复杂度：O(nlogn)。

  T(n) = 2T(n/2) + θ(n)   (递归加一次遍历）

有主定理(见另外一篇随笔)得：O(nlogn)。

 

稳定性：不稳定，原因如下：

举个例子：
待排序数组:int a[] ={1, 2, 2, 3, 4, 5, 6};

在快速排序的随机选择比较子(即pivot)阶段：

若选择a[2]（即数组中的第二个2）为比较子，，而把大于等于比较子的数均放置在大数数组中，则a[1]（即数组中的第一个2）会到pivot的右边， 那么数组中的两个2非原序（这就是“不稳定”）。

若选择a[1]为比较子，而把小于等于比较子的数均放置在小数数组中，则数组中的两个2顺序也非原序

这就说明，quick sort是不稳定的。

 

算法优化：

1.与归并排序类似，对于小数组，由于快排递归调用，增加了调用函数开销，此时采用插入排序更好；

2.使用子数组的一小部分元素的中位数切分数组，而非随机选数组第一个元素。

 

 

补充：三向切分：适用于含有大量重复KEY值情况。

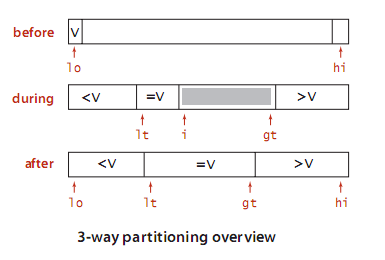
//三向切分
void three_direction_sort(int a[], int lo, int hi)
{
   if(hi < lo) return;
   int lt = lo, i = lo+1, gt = hi;
   int v = a[lo];    //base element
   while(i <= gt)
   {
      if(a[i] < v) exch(a,lt++,i++);
      else if(a[i] > v) exch(a,i,gt--);
      else i++;
   }  //now, a[lo...lt-1] < v = a[lt...gt] < a[gt+1...hi]
   three_direction_sort(a,lo,lt-1);
   three_direction_sort(a,gt+1,hi);
}

若看不懂，请到：https://www.bilibili.com/video/av9017598/?p=8

观看动画演示。