动态规划

从斐波那契数列看动态规划

斐波那契数列：f（n ）= f(n-1) + f(n-2)

分别用递归和非递归的方法来求解斐波那契数列的第n项。

def fabnacci(n):
    if n == 1 or n == 2:
        return 1
    else:
        return fabnacci(n - 1) + fabnacci(n - 2)


def fabnacci_no_recursive(n):
    fn = [0, 1, 1]

    for i in range(n - 2):
        fn.append(fn[-1] + fn[-2])
    return fn[-1]


# print(fabnacci(100))
print(fabnacci_no_recursive(100))

基于递归的方法存在子问题的重复计算，所以第n项的计算速度很慢。

钢条切割问题

某钢铁公司出售钢条的价格和钢条长度有以下关系 ：

问题：现在有一段长度为n的钢条，按照以上价格表出售，求使得收益最大的切割钢条方案。

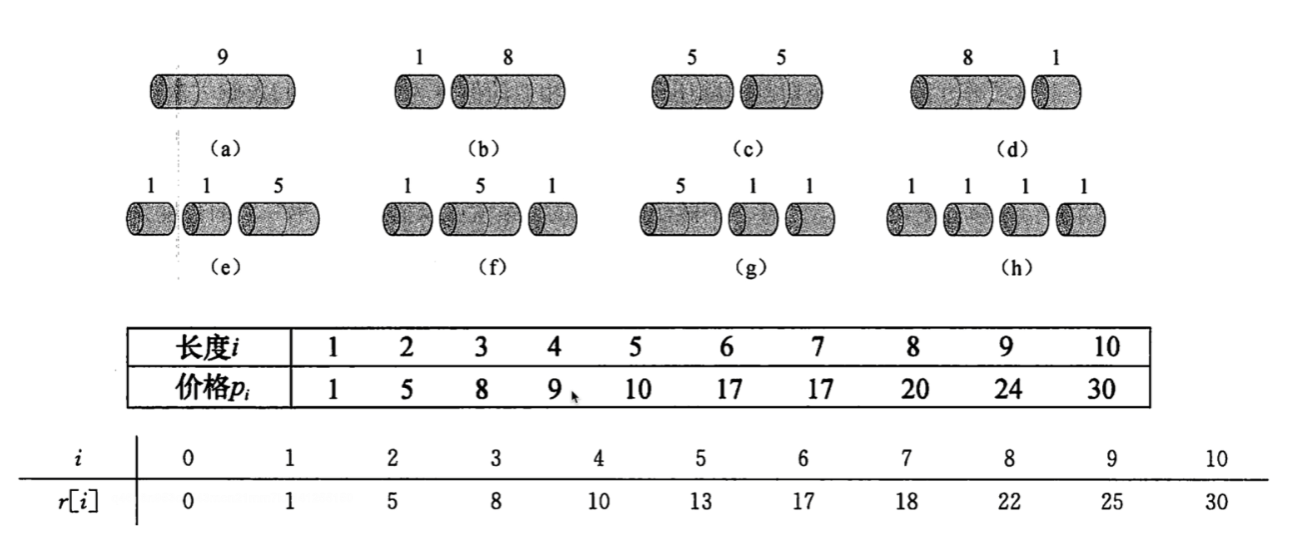
方案：

设长度为 n 的钢条切割后最优收益值为 r[n], 可以得出递推式：

第一个参数p_n表示不切割，

其他n-1个参数表示另外n-1种不同的切割方案，对于方案 i=1，2，。。。，n-1

将钢条切割为长度为 i 和 n-i 两段

方案 i 的收益为切割两段的最优收益之和

考虑所有的i，选择收益最大的为最优方案。

满足最优子结构，问题的最优解由相关子问题的最优解组合而成，这些子问题可以独立求解。

import time

priprice_list = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]


def cal_time(fun):
    def inner(*args, **kwargs):
        start_t = time.time()
        res = fun(*args, **kwargs)
        end_t = time.time()
        print(f"{fun.__name__}耗时:{end_t - start_t}")
        return res

    return inner


def cut_rod_recursive(p, n):
    if n == 0:
        return 0
    else:
        res = p[n]
        for i in range(1, n):
            res = max(res, cut_rod_recursive(p, i) + cut_rod_recursive(p, n - i))
        return res

@cal_time
def c1(p, n):
    return cut_rod_recursive(p, n)


def cut_rod_resursive2(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1, n + 1):
            res = max(res, p[i] + cut_rod_recursive(p, n - i))
        return res


@cal_time
def c2(p, n):
    return cut_rod_resursive2(p, n)

@cal_time
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n+1):
        res = 0
        # 遍历i种方案
        for j in range(1, i+1):
            res = max(res, p[j] + r[i-j])
        r.append(res)
    return r[n]

def cut_rod_extend(p, n):
    r = [0]
    s = [0]
    for i in range(1, n + 1):
        res = 0
        res_cut = 0
        # 遍历i种方案
        for j in range(1, i + 1):
            if res < p[j] + r[i - j]:
                res = p[j] + r[i - j]
                res_cut = j
        r.append(res)
        s.append(res_cut)
    return r[n], s

def solution(p, n):
    sol = []
    r, s = cut_rod_extend(p, n)
    while n > 0:
        sol.append(s[n])
        n -= s[n]
    return r, sol

print(solution(priprice_list, 15))