堆排序
1.树的概念

(1)树是一种数据结构
(2)树是一种可以递归定义的数据结构
(3)树是由n个节点组成的集合
n > 0, 存在一个节点是根节点,其他节点可以分为m个集合,每一个集合本身又是一棵树。
2.二叉树
概念
定义:每个节点最多有两个子节点,两个子节点被区分为左子节点和右子节点。
满二叉树:每一层的子节点都达到最大数。
完全二叉树:叶子节点只能出现在最下层和次下层,并且最下层的结点集中在最左边的若干个位置上
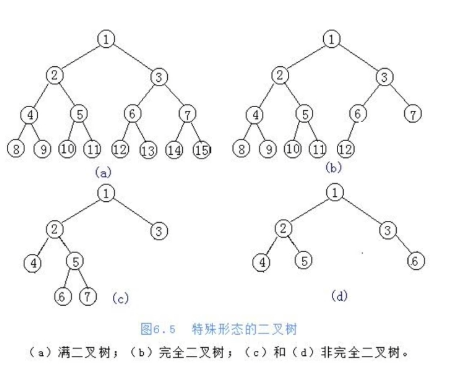
二叉树的顺序存储方式
父节点与两个子节点的关系:
父节点坐标是 i ,则左子节点是2i+1,右子节点是2i+2
例如:
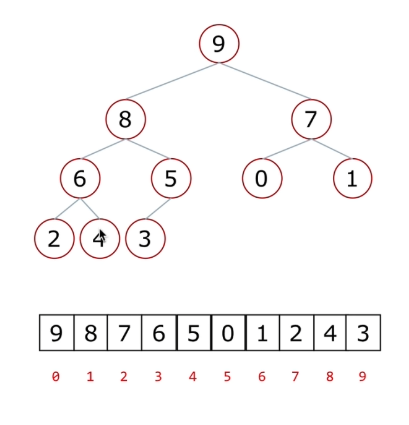
3.堆
什么是堆:是一种特殊的完全二叉树。
大根堆:一颗完全二叉树,满足任何一个子节点都比父节点小
小根堆:一颗完全二叉树,满足任何一个子节点都比父节点大
示例:
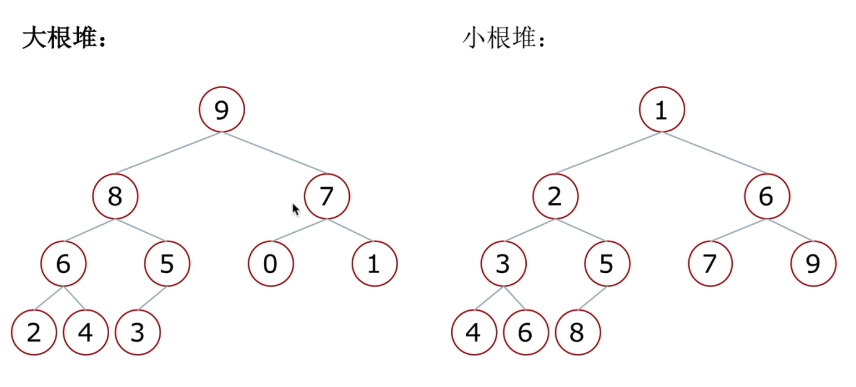
堆的向下调整的前提是:在二叉树中,只有一个位置不满足堆的性质,其它位置都满足堆的性质。
向下调整 是让调整的结点与其孩子节点进行比较。
4.堆排序过程
1.建立堆;
2.得到堆顶元素,即最大值;
3.去掉堆顶, 将堆的最后一个元素放到堆顶,此时再通过一次向下调整,使堆重新有序;
4.得到堆顶元素,即第二大值;
5.重复步骤3,直到堆变空。
代码实现:
1 def adjust(li, start, last_leaf): 2 """ 3 用于调整父节点与子节点的位置,保证父节点大于子节点 4 :param li: 5 :param start: 起始父节点 6 :param last_leaf: 最后一个子节点 7 :return: 8 """ 9 i = start # i最开始指向根节点 10 son_big = 2 * i + 1 # son_big开始是左孩子 11 tmp = li[start] # 把堆顶存起来 12 while son_big <= last_leaf: # 只要son_big位置有数 13 if son_big+1 <= last_leaf and li[son_big+1] > li[son_big]: # 找到较大的子节点 14 son_big = son_big+1 15 if tmp < li[son_big]: # 如果子节点都大于跟节点,则将子节点变成根节点 16 li[i] = li[son_big] 17 i = son_big # 向下看一层 18 son_big = 2 * i + 1 19 else: # 如果子节点都小于跟节点,则将tmp放某一个父节点上 20 li[i] = tmp 21 break 22 else: 23 li[i] = tmp 24 25 def heapsort(li): 26 n = len(li) 27 # 第一步,建堆,从后向前调整父节点与子节点的位置后就建堆完成 28 for i in range((n-2)//2, -1, -1): 29 adjust(li, i, n-1) 30 31 for i in range(n-1, -1, -1): 32 li[0], li[i] = li[i], li[0] # 将最大值li[0]放最后, 33 adjust(li, 0, i-1) #这时候要调整的二叉树就不算刚刚放到最后的最大值了。 34 return li 35 36 a = [i for i in range(100)] 37 38 random.shuffle(a) 39 print(a) 40 sorted_list = heapsort(a) 41 print(sorted_list)

