强化学习之路二 人工智能数学基础-函数篇
一次函数:y=kx+b (k≠0)
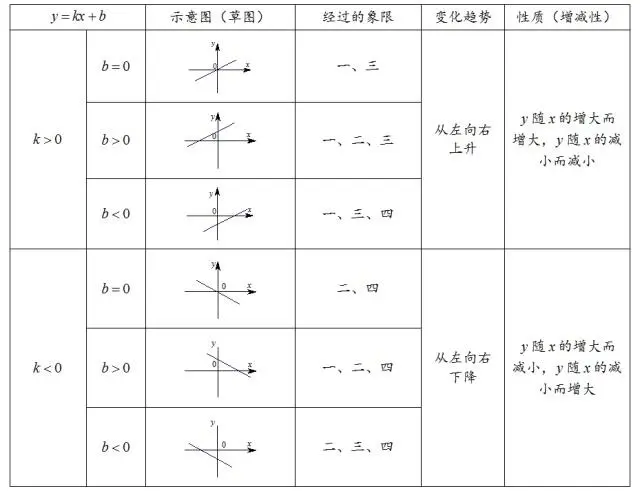
二次函数:y=ax2+bx+c (a≠0)
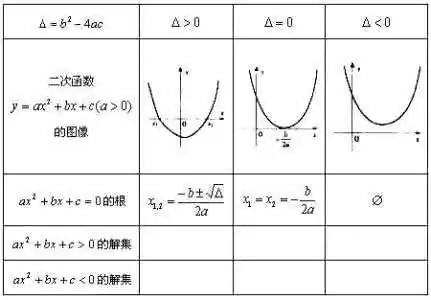
三次函数 y=ax3+bx2+cx+d (a≠0,b,c,d为常数)
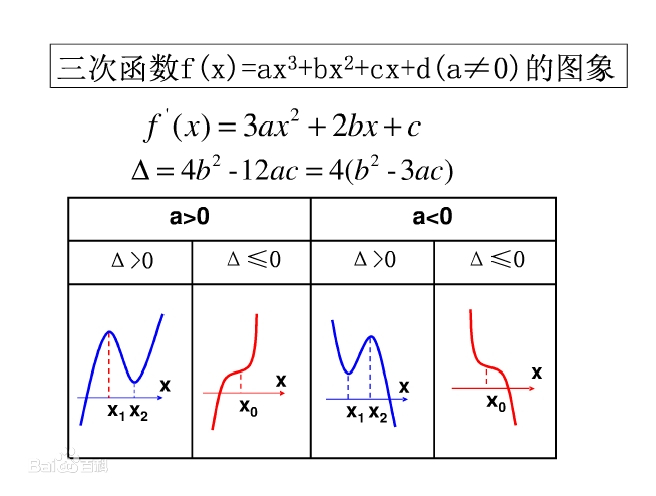
四次函数y=ax4+bx3+cx2+dx+e (a≠0,b,c,d,e为常数)
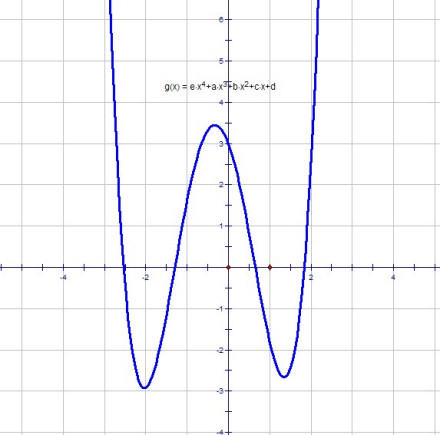
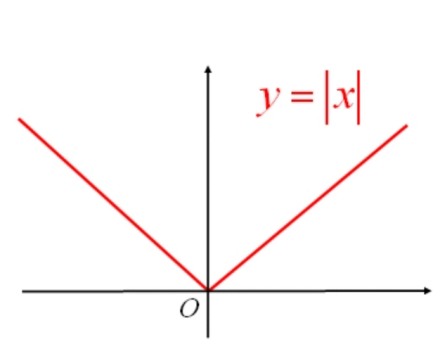
绝对值函数 y=∣x∣ 常作abs(x)
几何意义
∣x∣表示x轴上的点 x 到原点的距离
∣x―a∣表示x轴上的点 x 到点a的距离
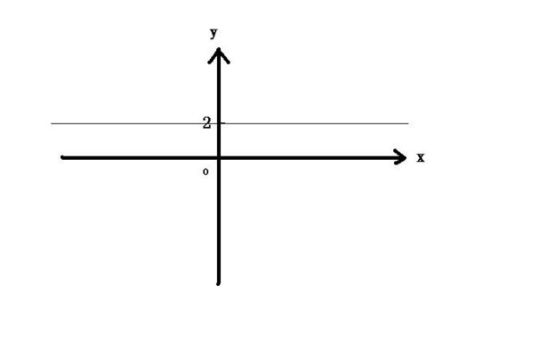
常数函数 f(x)=c
分段函数
分段函数,就是对于自变量x的不同的取值范围有不同的解析式的函数。它是一个函数,而不是几个函数;分段函数的定义域是各段函数定义域的并集,值域也是各段函数值域的并集
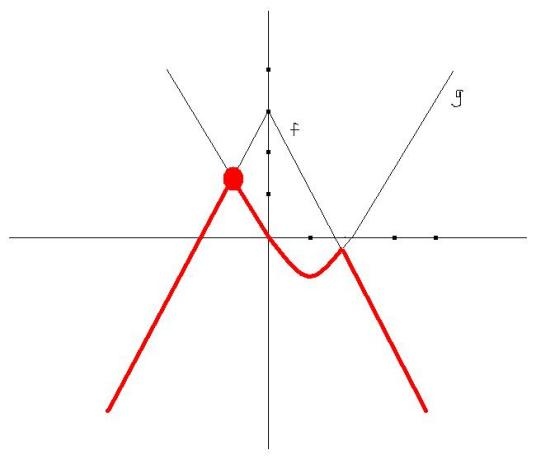
例子:
某商店卖西瓜,一个西瓜的重量若在4kg以下(包括4kg),则销售价格为0.6元/kg;若在4kg 以上,则销售价格为0.8元/kg,那么,一个西瓜的销售收入y元与重量xkg的函数关系表示为
y = 0.8x (>4)
y = 0.6x (0<x≤4)
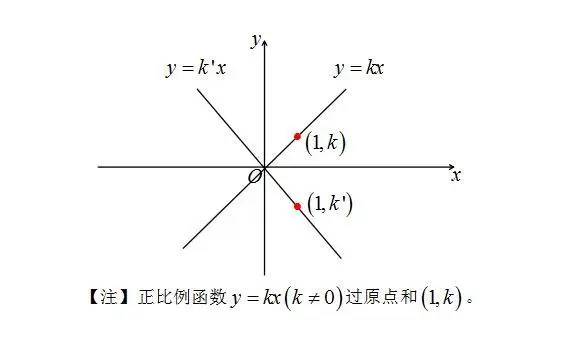
正比例函数 y=kx
正比例函数的图像是一条直线,通过原点,并且斜率为 k
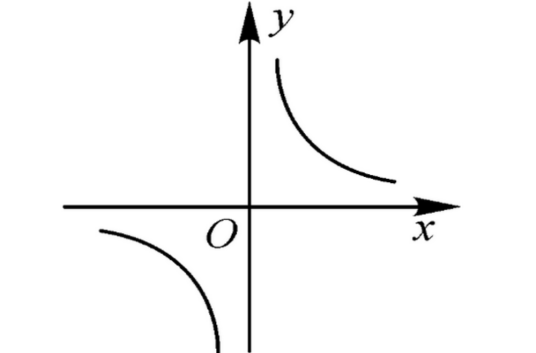
反比例函数 y=k/x (x≠0)
k的绝对值表示的是x与y的坐标形成的矩形的面积
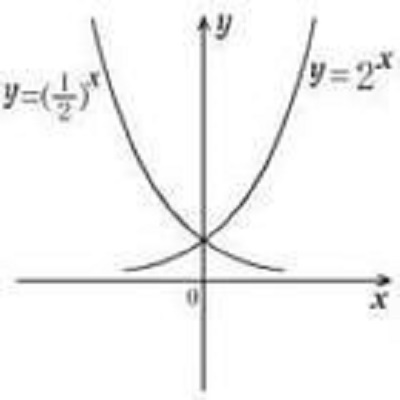
指数函数 y=a^x函数(a为常数且以a>0,a≠1)
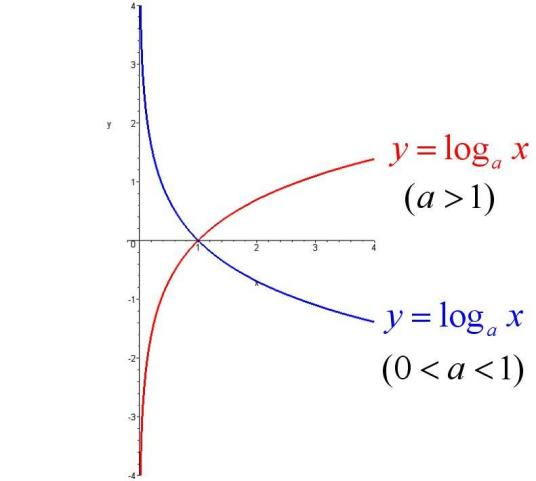
对数函数 \(f(x) = \log_a x\)(a>0 且 a≠1)
对数函数是指数的反函数
如果a=10, 可以省略不写
如果a=e=2.71828, 可以写成lnx
对应python: math.log(x[, a]) 底数是第二个参数
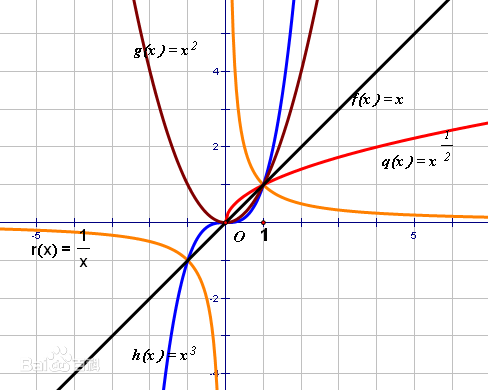
幂函数 \(f(x)=x^a\)
当\(a>0\)时,幂函数是单调递增的,因为\(x_1>x_2\)时,\(x_1^a>x_2^a\)。当\(a<0\)时,幂函数是单调递减的,因为\(x_1>x_2\)时,\(x_1^a<x_2^a\)。当\(a=0\)时,幂函数是常数函数\(f(x)=1\)
三角函数之正弦xián函数 f(x)=Asin(ωx+φ)
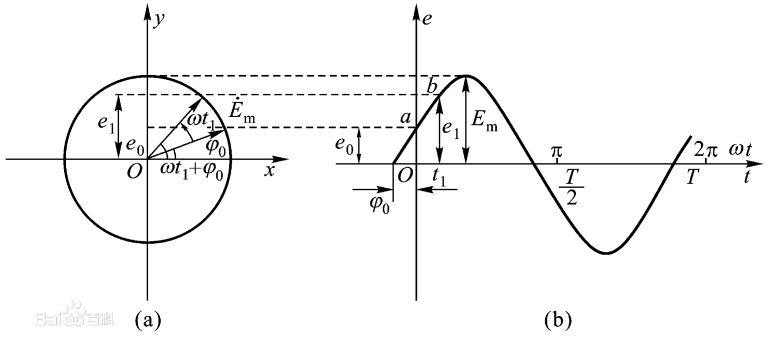
三角函数之余弦xián函数 f(x)=Acos(ωx+φ)
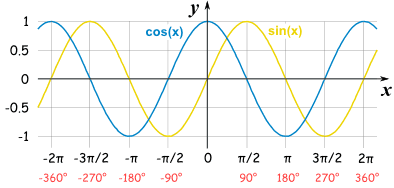
三角函数之正切函数 f(x) = tan(x) = sin(x)/cos(x)
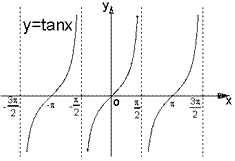
三角函数之反正弦函数 f(x)=arcsin(x)
python函数: math.asin()
定义域为[-1,1],值域为[-π/2,π/2] 反正弦函数是单调递增函数
sin(y) = x
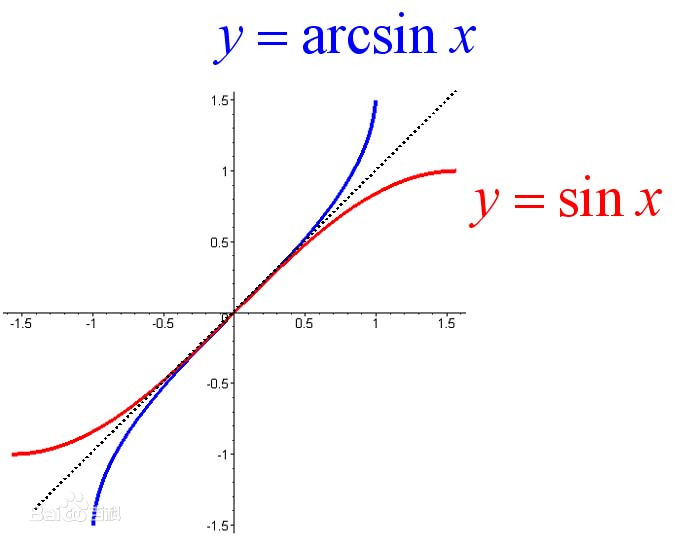
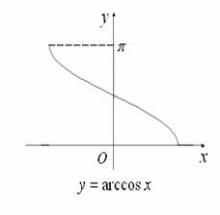
三角函数之反余弦函数 f(x)=arccos(x)
python函数: math.acos()
定义域为 [-1,1] 值域为 [0,π] 反余弦函数单调递减函数
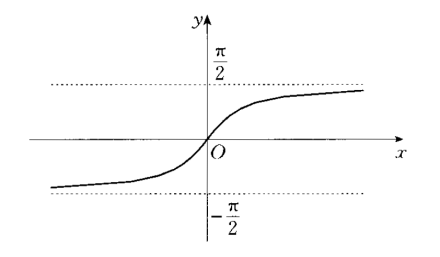
三角函数之反正切函数 f(x)=arctan(x)
python函数: math.atan()
定义域为R即(-∞,+∞) 值域为(-π/2,π/2) 反正切函数是单调递增函数, 奇函数
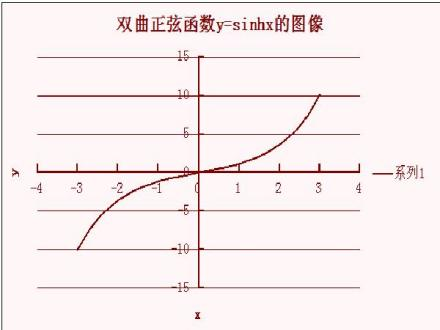
双曲函数之双曲正弦函数 f(x)=sinh(x)
\(sinh(x) = \frac{e^x - e^{-x}}{2}\)
python函数: math.sinh
定义域为(-∞,+∞) ,值域为(-∞,+∞) 单调递增函数, 奇函数
双曲函数之双曲余弦函数 f(x)=cosh(x)
\(cosh(x) = \frac{e^x + e^{-x}}{2}\)
python函数: math.cosh
定义域为(-∞,+∞) ,值域为(1,+∞)
是偶函数,x<0时递减, x>0时递增。 sinh(0) = 1

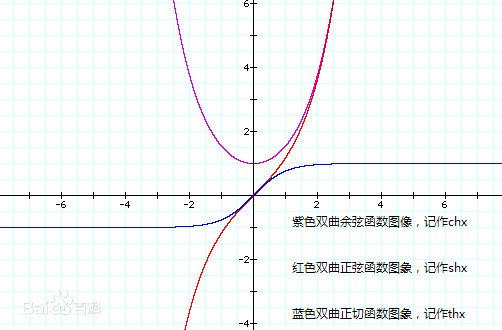
双曲函数之双曲正切函数 f(x)=tanh(x)
\(tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)
定义域为(-∞,+∞) ,值域为(-1,1) 单调递增, 奇函数
双曲函数之双曲余切函数
什么是反函数
反函数是指一个函数的输入和输出互换,即将原函数的输出作为输入,输出原函数的输入。如果一个函数的反函数存在,则该函数是可逆的。
有些函数没有反函数,这是因为它们不是一对一函数。一对一函数是指对于每个输入,都有唯一的输出。以下是一些常见的没有反函数的函数:
- y = x^2:这个函数不是一对一函数,因为对于一个x值,它有两个y值,一个是正的,一个是负的。
- y = sin(x):这个函数也不是一对一函数,因为对于不同的x值,它有相同的y值。
- y = |x|:这个函数也不是一对一函数,因为它不是单调递增或递减的。
- y = 0:这个函数对于任何x值都返回0,因此它没有反函数。 总之,只有当函数是一对一函数时,才有反函数。
什么是偶函数
什么是奇函数
常用数学函数图像:



