朴素贝叶斯

朴素贝叶斯

1. 算法流程

朴素贝叶斯算法（Naive Bayes, NB) 是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X求出使得后验概率最大的输出Y。NB模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单。当年的垃圾邮件分类都是基于朴素贝叶斯分类器识别的。

设有样本数据集D={d1,d2,...,dn}，对应样本数据的特征属性集为X={x1,x2,...,xd}类变量为Y={y1,y2,...ym} ，即D可以分为ym类别。其中{x1,x2,...,xd} 相互独立且随机，则Y的先验概率P(Y) ，Y的后验概率P(Y|X) ，由朴素贝叶斯算法可得，后验概率可以由先验概率P(Y) ,证据P(X) ,类条件概率P(X|Y)计算出

\[P(Y|X)=\frac{P(Y,X)}{P(X)}=\frac{P(X|Y)P(Y)}{\sum_{y \in F_Y} P(X|y)P(y)} \]

朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，上式可以进一步表示为下式：

\[P(X|Y=y)=\prod_{i=1}^dP(x_i|Y=y) \]

由以上两式可以计算出后验概率为：

\[P(Y|X) = \frac{\prod_{i=1}^dP(x_i|Y=y)P(Y)}{\prod_{i=1}^dP(x_i)} \]

其中\(P(Y|X)\)是后验概率，\(P(Y)\)是类别先验概率，\(P(X|Y)\)是似然概率，\(P(X)\)是归一化证据因子，与类别标签无关，因此\(P(Y|X)\)可以转化为\(P(X|Y)P(Y)\)。

以垃圾邮件分类为例， 假如你有一封邮件，包含：“代开,增值税,发票,sep”，这几个词，要预测其为垃圾邮件的概率，问题转化成P（垃圾|代开,增值税,发票,sep）只要计算出该表达式的值即可，应用全概率公式，进一步转换成下面的等式。

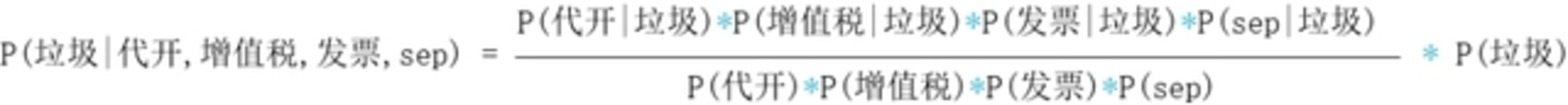
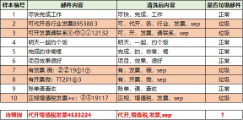
要计算上面的概率，需要我们有历史数据，于是我从我的邮箱里面复制了一些垃圾邮件，以及一些正常的邮件，并对数据做了一下简单的处理，打上了垃圾邮件和正常邮件的标签，我们就可以得到历史数据，进行计算了。

分子的概率计算,即垃圾邮件的条件下，各个词的概率：

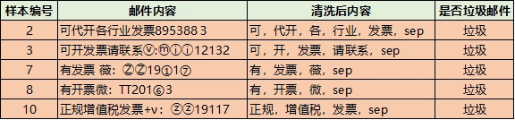
P（代开|垃圾） = 1/5 = 0.2

P（增值税|垃圾）= 1/5 = 0.2

P（发票|垃圾） = 4/5 = 0.8

P（sep|垃圾） = 5/5 = 1.0

分母概率计算，即全集中每个词的概率：

P（代开） = 1/10 = 0.1

P（增值税）= 1/10 = 0.1

P（发票） = 4/10 = 0.4

P（sep） = 5/10 = 0.5

计算垃圾邮件的概率，一共10个样本，5个垃圾邮件，5个正常邮件：

P(垃圾)= 5/10 = 0.5

汇总计算最后的垃圾概率：

P（垃圾|代开,增值税,发票,sep） = (0.2x0.2x0.8x1)x0.5/(0.1x0.1x0.4x0.5) = 0.8

我们计算下正常邮件的概率为多大，按公式直接计算，结果为0，但是直接计算，会导致很多样本都为0，所以后面会引入拉普拉斯平滑。

P（正常|代开,增值税,发票,sep） = 0

采用拉普拉斯变换计算得到，专门解决0概率问题：

P（代开|正常） = 1/（5+2） = 0.167

P（增值税|正常）= 1/（5+2） = 0.167

P（发票|正常） = 1/（5+2） = 0.167

P（sep|正常） = 1/（5+2） = 0.167

P（正常|代开,增值税,发票,sep）= (0.167x0.167x0.167x0.167)x0.5/(0.1x0.1x0.4x0.5) =0.194

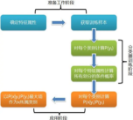
通过上述案例可以看到，贝叶斯算法的一个基本流程如下

2. 零概率问题

零概率问题，即测试样例的标签属性中，出现了模型训练过程中没有记录的值，或者某个分类没有记录的值，从而出现该标签属性值的出现概率 P(wi|Ci) = 0的现象。因为 P(w|Ci) 等于各标签属性值 P(wi|Ci) 的乘积，当分类 Ci 中某一个标签属性值的概率为 0，最后的 P(w|Ci) 结果也为 0。很显然，这不能真实地代表该分类出现的概率

解决方法：拉普拉斯修正，又叫拉普拉斯平滑，这是为了解决零概率问题而引入的处理方法。其修正过程：

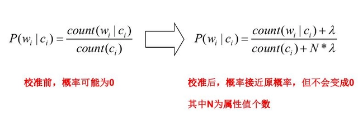
浮点数溢出问题：在计算 P(w|Ci) 时，各标签属性概率的值可能很小，而很小的数再相乘，可能会导致浮点数溢出。解决方法：对 P(w|Ci) 取对数，把概率相乘转换为相加。

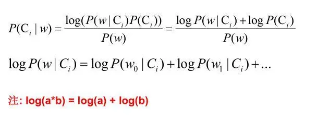
3. 连续性变量概率计算

对于离散型变量，直接统计频数分布就可以了。对于连续型的变量，为了计算对应的概率，此时又引入了一个假设，假设特征的分布为正态分布，计算样本的均值和方差，然后通过密度函数计算取值时对应的概率

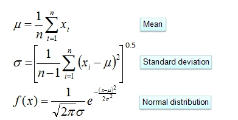
从上面的例子可以看出，朴素贝叶斯假设样本特征相互独立，而且连续型的特征分布符合正态分布，这样的假设前提是比较理想化的，所以称之为"朴素"贝叶斯，因为实际数据并不一定会满足这样的要求。

4. Scikit-learn库中的NB

在scikit-learn库，根据特征数据的先验分布不同，给我们提供了5种不同的朴素贝叶斯分类算法（sklearn.naive_bayes: Naive Bayes模块），分别是伯努利朴素贝叶斯（BernoulliNB），类朴素贝叶斯（CategoricalNB），高斯朴素贝叶斯（GaussianNB）、多项式朴素贝叶斯（MultinomialNB）、补充朴素贝叶斯（ComplementNB） 。

这5种算法适合应用在不同的数据场景下，我们应该根据特征变量的不同选择不同的算法，下面是一些常规的区别和介绍。

GaussianNB

高斯朴素贝叶斯，特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度。

这种模型假设特征符合高斯分布。

\[P(x_i|y) = \frac{1}{\sqrt{2 \pi \sigma_y^2}}e^{-\frac{(x_i-\mu_y)^2}{2\sigma_y^2}} \]

CategoricalNB

对分类分布的数据实施分类朴素贝叶斯算法，专用于离散数据集， 它假定由索引描述的每个特征都有其自己的分类分布。对于训练集中的每个特征 X，CategoricalNB估计以类y为条件的X的每个特征i的分类分布。样本的索引集定义为J=1,…,m，m作为样本数。

\[P(x_i=t|y=c;a)=\frac{N_{tic}+a}{N_c+an_i} \]

BernoulliNB

模型适用于多元伯努利分布，即每个特征都是二值变量，如果不是二值变量，该模型可以先对变量进行二值化，在文档分类中特征是单词是否出现，如果该单词在某文件中出现了即为1，否则为0。在文本分类的示例中，统计词语是否出现的向量(word occurrence vectors)(而非统计词语出现次数的向量(word count vectors))可以用于训练和使用这个分类器。BernoulliNB 可能在一些数据集上表现得更好，特别是那些更短的文档。如果时间允许，建议对两个模型都进行评估。

MultinomialNB

特征变量是离散变量，符合多项分布，在文档分类中特征变量体现在一个单词出现的次数，或者是单词的 TF-IDF 值等。不支持负数，所以输入变量特征的时候，别用StandardScaler进行标准化数据，可以使用MinMaxScaler进行归一化。

这个模型假设特征复合多项式分布，是一种非常典型的文本分类模型，模型内部带有平滑参数

ComplementNB

是MultinomialNB模型的一个变种，实现了补码朴素贝叶斯(CNB)算法。CNB是标准多项式朴素贝叶斯(MNB)算法的一种改进，比较适用于不平衡的数据集，在文本分类上的结果通常比MultinomialNB模型好，具体来说，CNB使用来自每个类的补数的统计数据来计算模型的权重。CNB的发明者的研究表明，CNB的参数估计比MNB的参数估计更稳定。