Vladik and Entertaining Flags
In his spare time Vladik estimates beauty of the flags.
Every flag could be represented as the matrix n × m which consists of positive integers.
Let's define the beauty of the flag as number of components in its matrix. We call component a set of cells with same numbers and between any pair of cells from that set there exists a path through adjacent cells from same component. Here is the example of the partitioning some flag matrix into components:
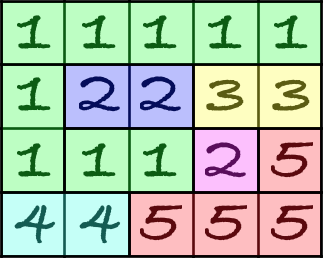
But this time he decided to change something in the process. Now he wants to estimate not the entire flag, but some segment. Segment of flag can be described as a submatrix of the flag matrix with opposite corners at (1, l) and (n, r), where conditions 1 ≤ l ≤ r ≤ m are satisfied.
Help Vladik to calculate the beauty for some segments of the given flag.
First line contains three space-separated integers n, m, q (1 ≤ n ≤ 10, 1 ≤ m, q ≤ 105) — dimensions of flag matrix and number of segments respectively.
Each of next n lines contains m space-separated integers — description of flag matrix. All elements of flag matrix is positive integers not exceeding 106.
Each of next q lines contains two space-separated integers l, r (1 ≤ l ≤ r ≤ m) — borders of segment which beauty Vladik wants to know.
For each segment print the result on the corresponding line.
4 5 4
1 1 1 1 1
1 2 2 3 3
1 1 1 2 5
4 4 5 5 5
1 5
2 5
1 2
4 5
6
7
3
4
Partitioning on components for every segment from first test case:
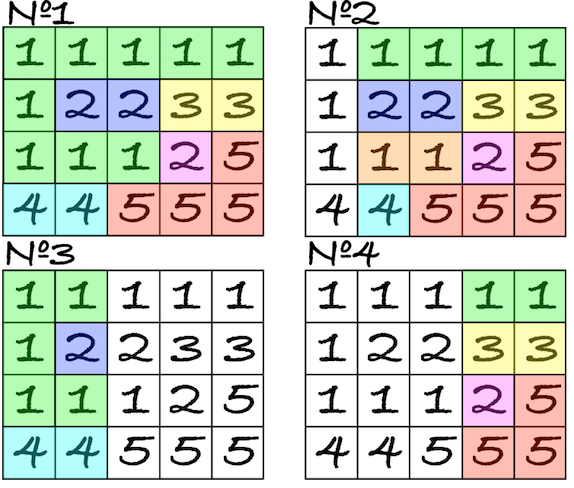
分析:给一个10*n矩阵,q次询问l到r内联通块个数;
用线段树维护区间,每个节点维护左右两边即可,合并区间时使用”并查集“实现;
代码:
#include <iostream> #include <cstdio> #include <cstdlib> #include <cmath> #include <algorithm> #include <climits> #include <cstring> #include <string> #include <set> #include <bitset> #include <map> #include <queue> #include <stack> #include <vector> #include <cassert> #include <ctime> #define rep(i,m,n) for(i=m;i<=n;i++) #define mod 1000000007 #define inf 0x3f3f3f3f #define vi vector<int> #define pb push_back #define mp make_pair #define fi first #define se second #define ll long long #define pi acos(-1.0) #define pii pair<int,int> #define sys system("pause") #define ls rt<<1 #define rs rt<<1|1 const int maxn=1e5+10; const int N=2e5+10; using namespace std; ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);} ll qpow(ll p,ll q){ll f=1;while(q){if(q&1)f=f*p%mod;p=p*p%mod;q>>=1;}return f;} int n,m,k,t,a[11][maxn],fa[41],id[41]; int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);} int Union(int x,int y) { x=find(x),y=find(y); if(x==y)return 0; return fa[x]=y,1; } struct node { int s[21]; int cnt; }s[maxn<<2]; void pup(node &s,node l,node r,int pos) { s.cnt=l.cnt+r.cnt; for(int i=1;i<=4*n;i++)fa[i]=i,id[i]=0; for(int i=1;i<=n;i++) { if(a[i][pos]==a[i][pos+1])s.cnt-=Union(l.s[i+n],r.s[i]+2*n); } int cnt=0; for(int i=1;i<=n;i++) { int &x=id[find(l.s[i])]; if(!x)x=++cnt; s.s[i]=x; int &y=id[find(r.s[i+n]+2*n)]; if(!y)y=++cnt; s.s[i+n]=y; } return ; } void build(int l,int r,int rt) { if(l==r) { s[rt].cnt=0; for(int i=1;i<=n;i++) { if(a[i][l]!=a[i-1][l]) { s[rt].cnt++; } s[rt].s[i]=s[rt].s[i+n]=s[rt].cnt; } return ; } int mid=l+r>>1; build(l,mid,ls); build(mid+1,r,rs); pup(s[rt],s[ls],s[rs],mid); } node gao(int L,int R,int l,int r,int rt) { if(L==l&&R==r)return s[rt]; int mid=l+r>>1; if(R<=mid)return gao(L,R,l,mid,ls); else if(L>mid)return gao(L,R,mid+1,r,rs); else { node x=gao(L,mid,l,mid,ls); node y=gao(mid+1,R,mid+1,r,rs); node ret; pup(ret,x,y,mid); return ret; } } int main() { int i,j; int q; scanf("%d%d%d",&n,&m,&q); rep(i,1,n)rep(j,1,m)scanf("%d",&a[i][j]); build(1,m,1); while(q--) { int l,r; scanf("%d%d",&l,&r); printf("%d\n",gao(l,r,1,m,1).cnt); } return 0; }





