面向对象第一单元总结
1.整体综述:
第一单元的作业内容为字符串表达式的化简,涉及到了字符串的处理、表达式的化简(如去除括号,因子相乘以及合并同类项),整体构造上采用递归下降的方式,分作表达式因子、项、因子的三种类型读取表达式。
2.第一次作业:
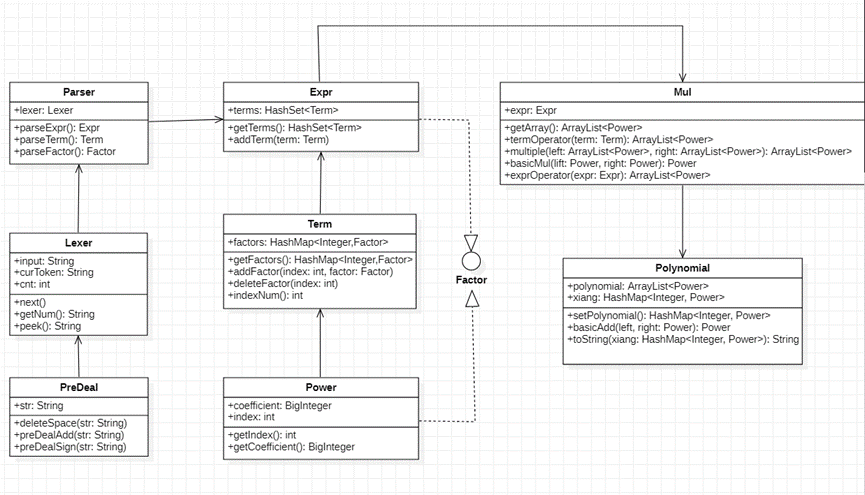
首先利用PreDeal类来预处理从输入中读到的字符串,包括去除多余的空格符、重复的加减号以及幂次后的符号,将处理好的字符串交给Lexer类,Lexer类进行字符串的读入工作,判断接下来的反馈内容,如数字、字母、符号等(第三次作业中会出现三角函数和嵌套自定义函数),并且将每一次读到的内容传递给Parser类。
Parser类进行字符串表达式的解析工作,利用Lexer读取字符串,这里采用了递归下降的方法,开始时是解析表达式因子,表达式因子由项相加组成,故将因子类Expr视作项的集合,用容器HashMap封装,由于第一次作业只有x及x的幂函数,最后所有的因子都可以表示成 系数*x**指数 的形式,这里将指数作为HashMap的key,系数作为值,好处是在将来进行因子乘法的时候可以直接将key值相加,值相乘,进行因子合并同类项时可以通过寻找相同的键值来判断是否需要合并。
通过递归下降的方式从表达式层读到项层,再读到因子层(项是一堆因子相乘,故项也可以用因子的集合表示)。因为可能会出现括号因子,括号内的内容为表达式,故表达式同样为因子,所以建立一个因子类,表达式类和Power类均为其接口,这样就实现了字符串的解析。
字符串的结构解析好之后需要进行拆括号的处理,拆括号是在项内进行,为避免某一类代码过长,这里重新建了一个Mul类用来处理因子乘法,对于每一对相乘的因子,首先判断其是Power类还是Expr类,建立两个ArrayList容器分别保存里面的内容,通过multiple方法进行乘积运算,返回值为一个项,调用basicMul来计算两个因子相乘,返回一个新的因子。
处理好括号之后,得到一个仅为Power构成的HashMap,理论上说这样的结果直接输出是可以直接通过测试点的,为了进一步化简我们还可以进行合并同类项的操作。使用之前所述的方法匹配键值,将对应的值相加,删去处理过的因子,最后得到的结果就是最终的输出。
输出时也可以进行一部分小优化,比如说系数为0、1、-1的情况以及指数为0可以直接输出1,指数为1可以不输出指数。
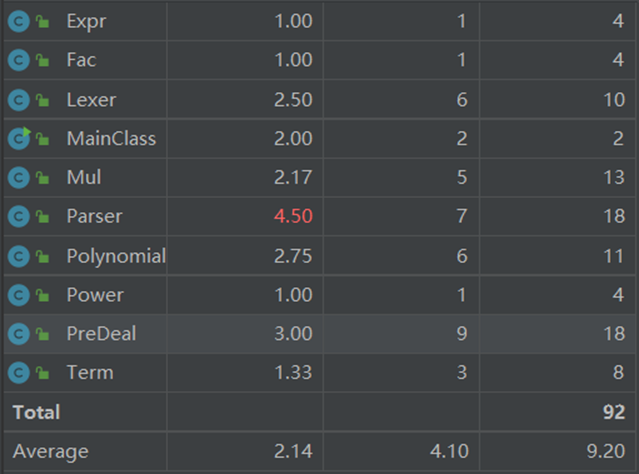
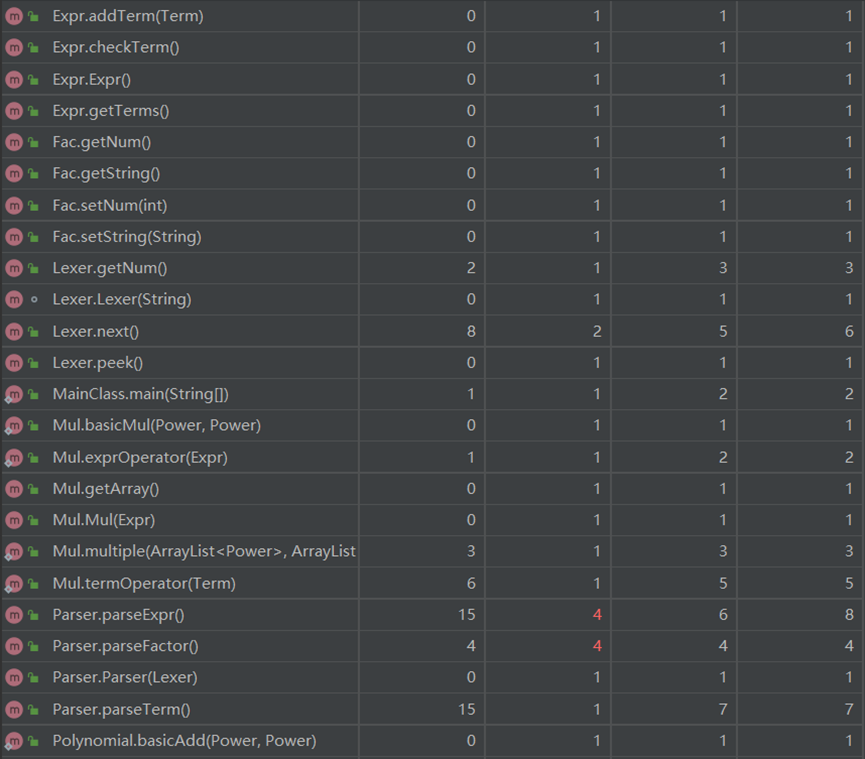
代码复杂度较高处主要出现在Parser类中,问题在于部分代码耦合度较高,可以尝试多写一个方法来减少出现过多重复冗余。
3.第二、三次作业:
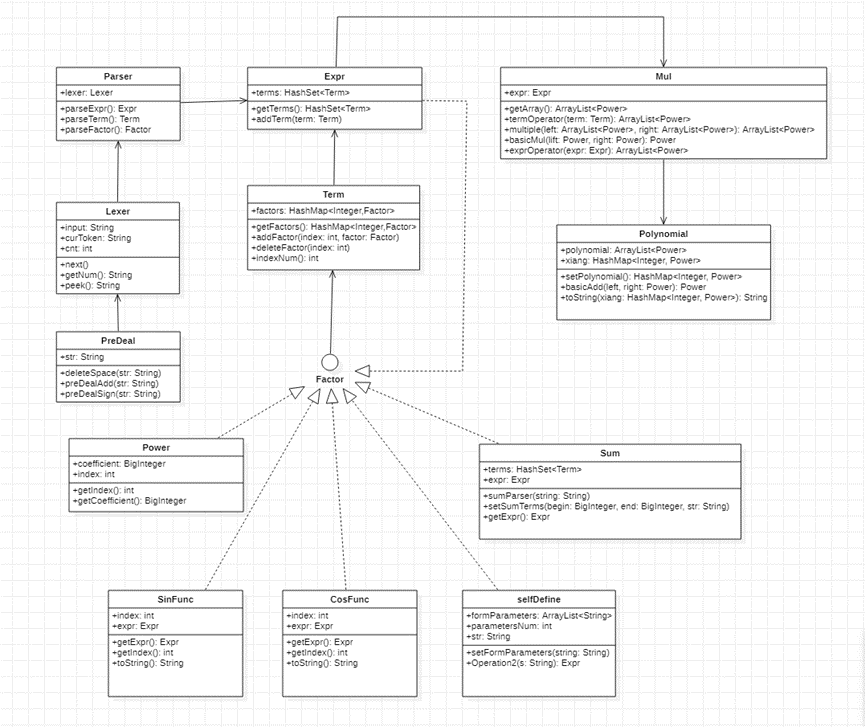
与第一次作业相比,二三次作业的不同在于加上了求和函数、自定义函数、以及三角函数类,这些类都应该被视作因子,故除了增添这几个类,还应该对解析类Parser,因子乘法类进行修改。
对于Parser类,我们需要根据关键字判断是否为特殊的因子,如果读到三角函数时,我采用的方法是将括号内的内容一律视作表达式因子,通过再调用一次PreDeal、Lexer、Parser的过程解析括号内的部分,故三角函数因子由两部分构成,一个是括号内的因子,另一个是三角函数自身的指数。如果读到自定义函数时,因为题目描述中只含有f、g、h三种函数名,可以通过HashMap容器,将函数名视作key,函数因子视作值来调用函数,需要一提的是,函数并不是简单的表达式替换,在第二次作业中我采用了表达式替换的replace方法,存在像x**2**2的情况,这种情况有一种解决办法是在替换时补上括号,如(x**2)**2,这样对于部分测试点不会出错,但仍然可能存在问题,故第三次作业改成了表达式建模的方法,这种方法更加清晰直观,不易出错。
之后还需要修改乘法类,在这个部分我采用了将三角函数前面的部分全部toString,通过比较两个字符串是否相等来判断是否在作乘法时可以合并,在加法处也是采取了同样的思路,这种实现方法可能过程比较复杂,并且在生成字符串和比较时可能会因为一些意想不到的问题而出错,另外,直接生成字符串可能会因为顺序的不同而判定为两个不同的字符串,故而需要在比较之前将每一个项都按照一定的顺序进行排序,比较排序后的结果。
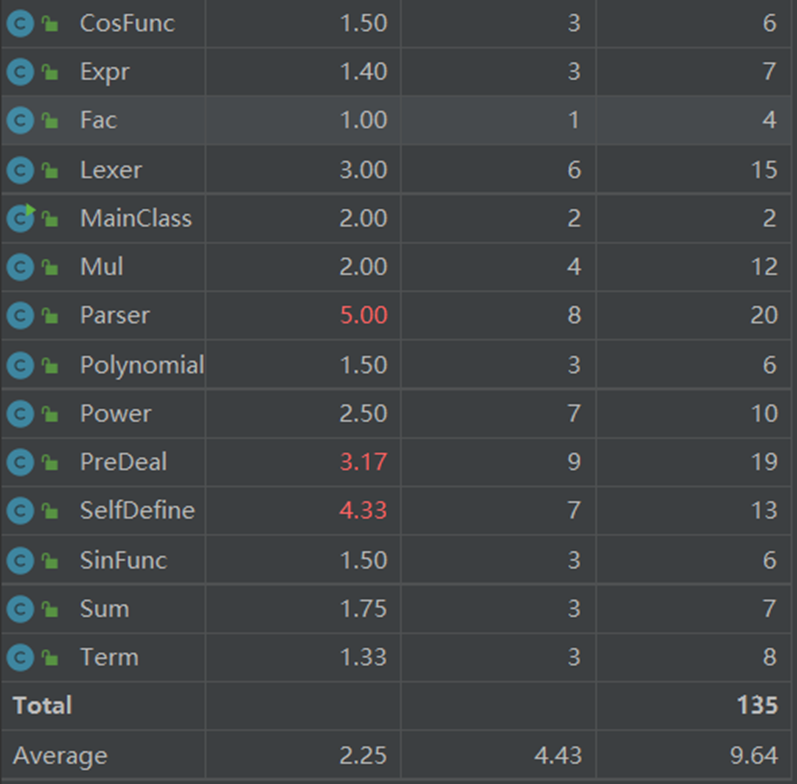
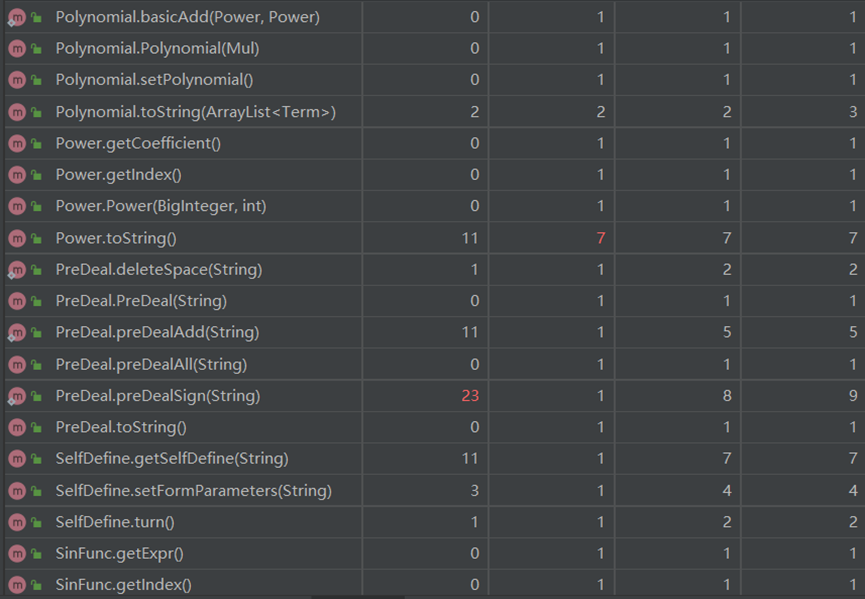
对于二三次作业的复杂度分析,相比第一次来说增加了PreDeal和SelfDefine部分,原因在于我刚写完代码的时候忘记重新预处理括号内的内容,导致强测出现了很多的bug(qwq)。在重新完成相关部分的时候,每一个新生成的字符串我都经过了新的PreDeal,导致代码的耦合部分过多,应该在对应的类中写一个专门用来预处理和解析字符串的方法以降低耦合度
4.Bug分析:
第一次作业中应为评测点相对来说比较简单的缘故,并未出现bug,到了二三次作业中因为疏忽出现的相对较多。
首先是在编写中自己发现的bug,在求和函数和自定义函数中,原本我使用的方法是通过利用String类的split方法按照‘,‘分割参数,但存在的问题就是假如参数中含有自定义函数或者求和函数时就会发生错误,因此我采用了栈来帮助读入的方法,记录到读到前括号的个数,读到一个前括号就令cnt加一,读到后括号就令cnt减一,只有cnt等于零的时候遇见逗号才进行参数的分离,相当于手写了一个split方法。
之后是对字符串替换后新生成的表达式未初始化的问题,这个问题直接让我倒在了强测上。
值得一提的是,我第二次作业一开始并不是采用了上述的构造诸多因子类的方法,而是将三角函数、幂函数统一在了一个Power类中,如以下代码所示:
private final BigInteger coefficient; //系数
private final int index; //指数
private final long[] sinIndex;
private final long[] cosIndex;
private HashMap<BigInteger, Long> sinCoeff = new HashMap<>();
private HashMap<BigInteger, Long> cosCoeff = new HashMap<>();
public Power(BigInteger num, int index, long[] sinIndex, long[] cosIndex) {
this.coefficient = num;
this.index = index;
this.sinIndex = sinIndex;
this.cosIndex = cosIndex;
}
public void addSinCoeff(BigInteger sinCoeffNum, long sinCoeffIndex) {
sinCoeff.put(sinCoeffNum,sinCoeffIndex);
}
public void addCosCoeff(BigInteger cosCoeffNum, long cosCoeffIndex) {
cosCoeff.put(cosCoeffNum,cosCoeffIndex);
}
public int getIndex() {
return index;
}
public BigInteger getCoefficient() {
return coefficient;
}
public long[] getCosIndex() {
return cosIndex;
}
public long[] getSinIndex() {
return sinIndex;
}
public HashMap<BigInteger, Long> getSinCoeff() {
return sinCoeff;
}
public HashMap<BigInteger, Long> getCosCoeff() {
return cosCoeff;
}
public void setCosCoeff(HashMap<BigInteger, Long>
cosCoeff) {
this.cosCoeff = cosCoeff;
}
public void setSinCoeff(HashMap<BigInteger, Long>
sinCoeff) {
this.sinCoeff = sinCoeff;
}
我在Power类中建立了两个数组分别表示不同三角函数的指数,这是一个取巧的办法,因为题目中规定了幂函数的幂次不会超过8,因此最多只有八种带幂函数的三角函数外加括号内是常数的三角函数,再利用HashMap记录常数三角函数,就可以将所有的因子归结到一个Power类中进行表示。
但这种方法面对的问题就是无法表示嵌套三角函数的情况、无法表示三角函数内的表达式可取任意值的情况、无法处理增添新类型因子比如对数函数、指数函数的情况,因此仅仅只是在特定的要求下的一种简便方法,不过这种方法实现起来相对简单,尤其是在处理因子乘法和加法的时候,同第一次作业的差别不大。
5.优化分析:
在本次作业中未实现过多的优化(主要是优化实在是太多的bug了,不敢交上去…),但是对于优化有过一定的思考和尝试。
优化集中在三角函数上,一个是合并二倍角,这种优化只需要在项的内部进行,相对来说比较简单,首先建立一个ArrsyList容器保存每一个三角函数toString的结果,接着遍历这个容器寻找有无括号内内容相同、三角函数名不同的情况,有的话记录位置,将原本的两个因子删除,使用新的因子进行代替,这里存在连两个问题,一个是必须要两个三角函数的幂次相同的时候,因为存在一种情况是sin(x)**2*cos(x),通过二倍角化简的结果为2*sin(x)*sin(2*x),可以明显的发现二倍角化简后的结果比原来的结果还要更长,显然这是不能增加性能的。第二个问题是这种方法只能实现一遍遍历,比如后面利用二倍角化简得到的见过不能和之前的相匹配,不过这样可以通过写递归函数再次遍历,利用标记数标记是否存在可以化简的项来解决。
第二种化简是sin(x)**2+cos(x)**2 = 1。这种化简比较复杂,我尝试了两种方法,第一种是将所有的cos全部用上述公式替换成sin,之后重新合并同类项,获得输出的字符串长度与原来的化简前的字符串长度进行比较,这种方法的效率很低。第二种方法是在同学的启发下写的,我们可以先将某一项中的cos平方全部替换成sin,通过比较是否出现了相同的项来判断需不需要化简,这种方法的好处在于实现过程较为简单,缺点是同样需要多次遍历判断是否优化完全。
6.心得体会
第一单元以迭代式开发的方式完成了字符串表达式解析,初步感受到了面向对象语言的独特思路以及工程代码编写的流程。在实际完成过程中明显的感觉到了语法知识不牢固,一些java自带类中的方法应用不熟练,还处在边用边查资料的阶段,代码还保留了一部分C语言中面向过程式编程的方法,部分类的耦合度较高。希望在下次作业中不会出现专门为了实现方法而构造的类,而是将方法自然地融入到类中。




