5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

 

 

 

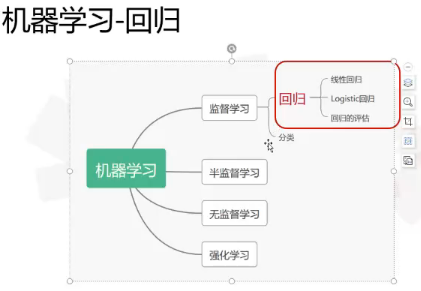
监督学习：监督学习是从标记的训练数据来推断一个功能的机器学习任务。

半监督学习：半监督学习使用大量的未标记数据，以及同时使用标记数据，来进行模式识别工作。

 

无监督学习：根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题，称之为无监督学习。

 

 

 

 

最小二乘法：

　　线性回归都可以通过最小二乘法求出其方程，可以计算出对于y=bx+a的直线。

 

 

import random
import matplotlib.pyplot as plt
 
xs = [0.1*x for x in range(0, 10)]
ys = [12*i*4 for i in xs]
print(xs)
print(ys)
 
w = random.random()
b = random.random()
a1 = []
b1 = []
 
for i in range(10):
    for x, y in zip(xs, ys):
        o = w*x+b   # 预测值
        e = (o-y)
        loss = e**2  # 损失值
        dw = 2*e*x
        db = 2*e*1
        w = w-0.1*dw
        b = b-0.1*db
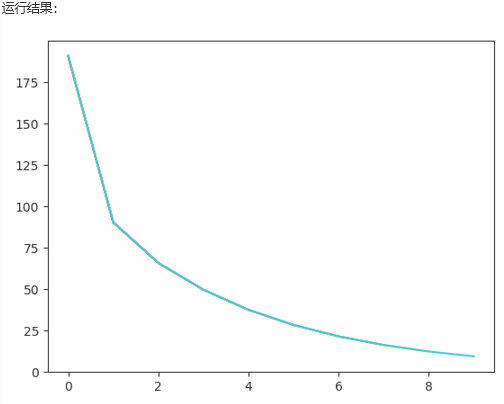
        print('loss={0},w={1},b={2}'. format(loss, w, b)) # 损失值越小越好
    a1.append(i)
    b1.append(loss)
    plt.plot(a1, b1)
    plt.pause(0.1)
plt.show()

 

2.思考线性回归算法可以用来做什么？

　　切合生活实际来说，它可以简单地预测房价数据；

　　学习中最常见的就是应用于数学；

　　像现如今，在疫情传播严重的新冠病毒也是能应用于一些观察性研究。

 

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。

　　自己爬的一组二手车网的数据，部分如下：

 

 

源代码

　　这次取其中的油耗/L和百公里油耗/L来进行线性回归方程实验

import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv('./201706120033 段泽平.csv', index_col=0)  # 数据读取
data.dropna(inplace=True)

# 线型回归
from sklearn.linear_model import LinearRegression           #导入线性回归方程包

regr = LinearRegression()  # 模型构建
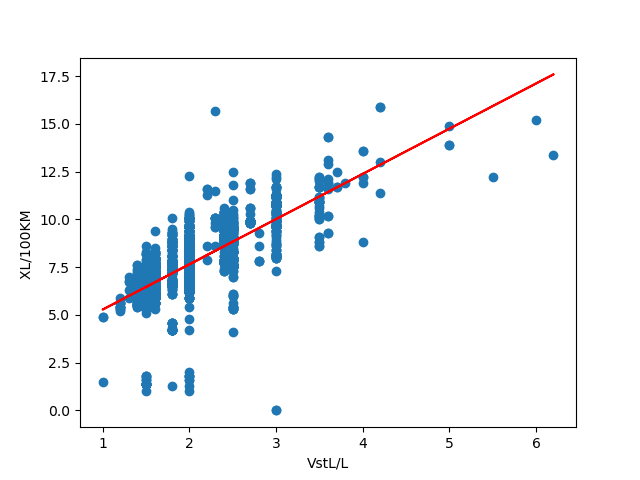
regr.fit(data[['排量/L']], data['百公里油耗/L'])
print('权值：', regr.coef_, '截距：', regr.intercept_)

plt.scatter(data['排量/L'].values, data['百公里油耗/L'].values)
plt.plot(data[['排量/L']].values, regr.predict(data[['排量/L']].values), c='r')
plt.xlabel('VstL/L')
plt.ylabel('XL/100KM ')

 

运行结果：