【学习笔记】卡特兰数
【学习笔记】卡特兰数
基本概念
问题引入:网格行走问题
在一个平面直角坐标系内,你位于 \((0, 0)\),你想要走到 \((n, n)\) (\(n\geq 1\))。每步只能向右或向上走一单位长度。要求在任意时刻,你所处的坐标 \((x, y)\) 满足 \(x\geq y\)(也就是不能越过第一象限角平分线)。求有多少种合法的方案。
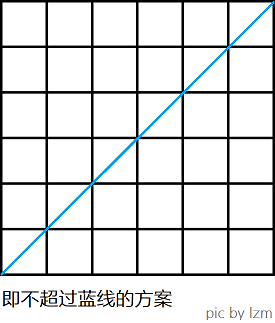
做法:如果不考虑“不能越过第一象限角平分线”的要求,那么总方案数显然是 \({2n\choose n}\),也就是在总共 \(2n\) 步中,任选出 \(n\) 步向上走(剩下的 \(n\) 步向右走)。
下面考虑减去不合法的方案。
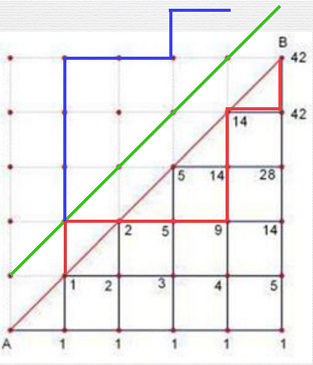
如果一种方案不合法,那这条路径上至少会有一个点,碰到了直线 \(y = x + 1\)。假设路径第一次碰到 \(y = x + 1\) 的点为 \(p\)。将 \(p\) 之后的路径(即从 \(p\) 到 \((n, n)\) 的路径)关于直线 \(y = x + 1\) 做对称。
如下图,绿线即 \(y = x + 1\),红线为原路径越过第一象限角平分线后的部分,蓝线为关于 \(y = x + 1\) 对称后的结果。
发现任何一条不合法的路径,对称后都唯一对应一条从 \((0, 0)\) 到 \((n - 1, n + 1)\) 的路径。并且,任何一条从 \((0, 0)\) 到 \((n - 1, n + 1)\) 的路径,也唯一对应了一条不合法的原路径(从第一次经过 \(y = x + 1\) 的点开始,对称回来,就能得到原路径了)。因此,二者之间是一一映射的关系。
所以,不合法的路径数量,就等于从 \((0, 0)\) 到 \((n - 1, n + 1)\) 的路径数量,即 \({2n\choose n + 1}\)。
所以答案就等于:
示意图:
定义:卡特兰数
它的前几项(从 \(c_0\) 开始)是:\(1\), \(1\), \(2\), \(5\), \(14\), \(42\), \(132\), \(429\), \(1430\), \(4862\) ...
定理1:卡特兰数的另一种形式
证明:
\[\begin{align} c_n &= {2n\choose n} - {2n\choose n + 1}\\ &= \frac{(2n)!}{n!n!} - \frac{(2n)!}{(n + 1)!(n - 1)!}\\ &= \frac{(2n)!\cdot (n + 1)!(n - 1)! - (2n)!\cdot n!n!}{n!n!(n + 1)!(n - 1)!}\\ &= \frac{(2n)!(n - 1)!n!\cdot ((n + 1) - n)}{n!n!(n + 1)!(n - 1)!}\\ &= \frac{(2n)!}{n!(n + 1)!}\\ &= \frac{1}{n + 1}\cdot \frac{(2n)!}{n!n!}\\ &= \frac{{2n\choose n}}{n + 1} \end{align} \]
定理2:卡特兰数的递推式
令 \(c_{0} = 1\),则对任意 \(n > 0\),有:
证明:
考虑上述的网格行走问题,我们枚举路径里(除起点外)第一次碰到直线 \(y = x\) 的点,设它的坐标为 \((i, i)\) (\(1\leq i\leq n\))。
那么从 \((0, 0)\) 走到 \((i, i)\) 的方案数,就相当于从 \((1, 0)\) 走到 \((i, i - 1)\) 且不越过直线 \(y = x - 1\) 的方案数(因为我们要保证 \((i, i)\) 是第一次碰到 \(y = x\),所以之前不能碰),即 \(c_{i - 1}\)。
从 \((i, i)\) 走到 \((n, n)\) 的部分,方案数显然是 \(c_{n - i}\)。
所以每个 \(i\) 贡献的方案数就是 \(c_{i - 1} \cdot c_{n - i}\)。
小练习:用生成函数方法,从【递推式】推出【定义式】。
几种常见的实际意义
- \(n\) 对括号的合法括号序列数。把左括号看做向右走,右括号看做向上走,则等价于上述的网格行走问题。
- \(n\) 个数入栈、出栈(以固定顺序入栈,在任意栈非空的时刻可以选择弹出一个数)得到的排列数。入栈即向右走,出栈即向上走,等价于网格行走问题。
- \(n\) 个节点的二叉树数量。观察上述递推式,相当于枚举左子树大小为 \(i - 1\),右子树大小为 \(n - i\)。
- \(n\) 层的阶梯切割为 \(n\) 个矩形的切法数(见「AHOI2012」树屋阶梯)。
再探网格行走问题
将【网格行走问题】中的终点从 \((n, n)\) 改为 \((n, m)\),保证 \(n\geq m\)。仍然要求在任意时刻你所处的坐标 \((x, y)\) 满足 \(x\geq y\)。求有多少种合法的方案。
做法:仍然考虑在第一次碰到直线 \(y = x + 1\) 时,将此后的路径关于 \(y = x + 1\) 对称。发现不合法的路径,与从 \((0, 0)\) 到 \((m - 1, n + 1)\) 的路径一一映射。所以答案就是
详见此题:「SCOI2010」生成字符串。
例题1:「HNOI2009」有趣的数列
题目大意:
我们称一个长度为 \(2n\) 的数列是有趣的,当且仅当该数列满足以下三个条件:
- 它是从 \(1 \sim 2n\) 共 \(2n\) 个整数的一个排列 \(\{a_n\}_{n=1}^{2n}\);
- 所有的奇数项满足 \(a_1 < a_3 < \dots < a_{2n-1}\),所有的偶数项满足 \(a_2 < a_4 < \dots < a_{2n}\);
- 任意相邻的两项 \(a_{2i-1}\) 与 \(a_{2i}\) 满足:\(a_{2i-1}<a_{2i}\)。
例如,\(n = 3\) 时共有 \(5\) 个有趣的数列:\((1,2,3,4,5,6)\), \((1,2,3,5,4,6)\), \((1,3,2,4,5,6)\), \((1,3,2,5,4,6)\), \((1,4,2,5,3,6)\)。
对于给定的 \(n\),请求出有多少个不同的长度为 \(2n\) 的有趣的数列。答案对一个给定的数 \(p\) 取模(注意,\(p\) 不一定是质数)。
数据范围:\(1\leq n\leq 10^{6}\),\(1\leq p\leq 10^{9}\)。
考虑将数字 \(1, 2,\dots, 2n\) 依次填入排列,使结果是有趣的。那么,我们每次一定会选择【最小的空奇数位】或【最小的空偶数位】。因为只有这样才能使得奇数项和偶数项分别递增。
但此时仍然不一定满足【\(\forall i: a_{2i-1}<a_{2i}\)】的要求。考虑如果存在 \(a_{2i - 1} > a_{2i}\),说明 \(2i - 1\) 这个位置上的数,填的时间比 \(2i\) 位置迟。也就是第 \(i\) 个奇数位填的时间比第 \(i\) 个偶数位迟。我们要避免这种情况,等价于保证在任意时刻【奇数位上的数的数量】\(\geq\)【偶数位上的数的数量】。
把【在奇数位填一个数】看做向右走一步,【在偶数位填一个数】看做向上走一步,那么原问题等价于【网格行走问题】。所以答案就是卡特兰数,即:\(\frac{{2n\choose n}}{n + 1}\)。
本题的另一个难点是,模数不一定是质数,不方便求逆元。考虑如何不使用除法。
考虑求出每个质数对答案的贡献(几次幂),再相乘。分别算出分子、分母里每个质数的次幂,然后相减即可(除法被转化为了减法!)。计算每个质数的次幂,我的做法是枚举所有 \(i\),并分解质因数。暴力分解质因数,单次的复杂度是 \(\mathcal{O}(\sqrt{n})\) 的,太慢了。可以先用线性筛预处理出每个数的最小质因子,这样在分解质因数时,可以省去不必要的枚举,单次分解的复杂度就是每个数的质因子数量,是 \(\mathcal{O}(\log n)\) 的,总时间复杂度 \(\mathcal{O}(n\log n)\)。
参考代码
// problem: P3200
#include <bits/stdc++.h>
using namespace std;
#define mk make_pair
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
template<typename T> inline void ckmax(T& x, T y) { x = (y > x ? y : x); }
template<typename T> inline void ckmin(T& x, T y) { x = (y < x ? y : x); }
const int MAXM = 2e6;
int n, MOD;
inline int mod1(int x) { return x < MOD ? x : x - MOD; }
inline int mod2(int x) { return x < 0 ? x + MOD : x; }
inline void add(int &x, int y) { x = mod1(x + y); }
inline void sub(int &x, int y) { x = mod2(x - y); }
inline int pow_mod(int x, int i) {
int y = 1;
while (i) {
if (i & 1) y = (ll)y * x % MOD;
x = (ll)x * x % MOD;
i >>= 1;
}
return y;
}
int p[MAXM + 5], cnt;
bool v[MAXM + 5];
int minp[MAXM + 5];
int f[MAXM + 5];
int main() {
cin >> n >> MOD;
int m = 2 * n;
for (int i = 2; i <= m; ++i) {
if (!v[i]) {
p[++cnt] = i;
minp[i] = i;
}
for (int j = 1; j <= cnt && p[j] * i <= m; ++j) {
v[p[j] * i] = 1;
minp[p[j] * i] = p[j]; // 最小质因子
if (i % p[j] == 0) {
break;
}
}
}
for (int i = n + 2; i <= m; ++i) {
int x = i;
while (x != 1) {
int y = minp[x];
while (x % y == 0) {
f[y]++;
x /= y;
}
}
}
for (int i = 2; i <= n; ++i) {
int x = i;
while (x != 1) {
int y = minp[x];
while (x % y == 0) {
f[y]--;
x /= y;
}
}
}
int ans = 1;
for (int i = 2; i <= m; ++i) {
if (!v[i]) {
assert(f[i] >= 0);
ans = (ll)ans * pow_mod(i, f[i]) % MOD;
}
}
cout << ans << endl;
return 0;
}
例题2:「NOI2018」冒泡排序
题目大意:
冒泡排序算法:
输入:一个长度为 n 的排列 p[1...n]
输出:p 排序后的结果。
for i = 1 to n do
for j = 1 to n - 1 do
if(p[j] > p[j + 1])
交换 p[j] 与 p[j + 1] 的值
可以证明,交换次数的一个下界是 \(\frac{1}{2}\sum_{i = 1}^{n}|i - p_i|\)。
称一个长度为 \(n\) 的排列是好的,当且仅当对它进行冒泡排序的交换次数恰好等于 \(\frac{1}{2}\sum_{i = 1}^{n}|i - p_i|\)。
给定一个长度为 \(n\) 的排列 \(q\)。求字典序严格大于 \(q\) 的好的排列数。答案对 \(998244353\) 取模。
数据范围:每个测试点有 \(5\) 组测试数据,每组测试数据满足 \(1\leq n\leq 6\times 10^5\),整个测试点满足 \(\sum n\leq 2\times 10^6\)。
发现,一个排列是好的,当且仅当不存在长度 \(\geq 3\) 的下降子序列。
考虑逐位构造一个好的排列,现在填到位置 \(i\),前 \(i-1\) 位的最大值为 \(\mathrm{mx}\)。则第 \(i\) 位要么填任意一个 \(> \mathrm{mx}\) 的数,要么填 $ < \mathrm{mx}$ 的最小的数(否则就一定会出现长度为 \(3\) 的下降子序列)。
于是想到 DP。设 \(\mathrm{dp}(i,j)\) 表示前 \(i\) 位的最大值是 \(j\) 的情况下,第 \(i+1\) 到第 \(n\) 位的填数方案。这样我们可以从后往前转移(或者用记忆化搜索实现),即:
特别地,如果 \(j < i\),则 \(\mathrm{dp}(i, j) = 0\)。
为什么要把 DP 数组定义成“第 \(i\) 位之后的填数方案”呢?因为这样便于我们处理字典序的问题。我们统计答案时,枚举从第 \(i\) 位开始,字典序第一次大于输入的排列 \(q\)(前 \(i-1\) 位全部和 \(q\) 相等)。设 \(\mathrm{mx}_i=\max_{j=1}^{i}q_j\),则:
答案就是所有 \(\mathrm{ans}_i\) 之和。
这样暴力 DP 是 \(\mathcal{O}(n^3)\) 的,用后缀和优化可做到 \(\mathcal{O}(n^2)\)。
继续观察这个 DP。发现 \(\mathrm{dp}(i, j)\) 就相当于在一个二维平面上,从点 \((i, j)\) 走到点 \((n, n)\) 的方案数。同时我们有一些要求:
- 每轮必须先向右走一步(也就是 \(i\to i + 1\))。
- 然后可以向上走若干步,或不向上走(也就是 \(j\to k\), \(k\geq j\))。
- 每轮结束时,需保证所在位置 \((i, j)\) 满足 \(i\leq j\)。
- 如此进行 \(n - i\) 轮之后,恰好到达点 \((n, n)\)。
称这样的 \(n - i\) 个“轮”,为一个“方案”。我们要计算满足上述要求的“方案”的数量。
直接对“方案”计数,其实就是上述 DP 的过程了。但我们要优化它,就必须跳出这个思路的局限。把方案里的所有“轮”拆散了看,它就是一条从 \((i, j)\) 走到 \((n, n)\) 的路径(这里和后文中所有“路径”都是指:每步只能向上或向右走一格),其中每向右走一步,就相当于开始了新的一轮。并且任意一条路径一定恰有 \(n - i\) 步是向右走的,因此我们不需要刻意地去划分出轮次,直接对路径计数即可。
具体来说,路径需要满足如下要求:
- 路径的第一步必须是向右走的:也就是 \((i, j)\to (i + 1, j)\),而不能是 \((i, j)\to (i, j + 1)\)。
- 在原来的“方案”里,要求每轮结束时满足 \(i\leq j\),但在过程中(比如说先向右走了一步,还没向上走之前)是不一定的。实际上,要求可以转化为:路径里不能存在 \((i, j) \to (i + 1, j)\) 且 \(i > j\),因为这一步是向右走的,意味着 \((i, j)\) 这一轮已经结束了。所以要求可以进一步转化为,整个路径中,不能存在 \(i - j\geq 2\)。
考虑如何统计满足上述两个要求的路径数。第 1 个要求很好实现,我们把起点设为 \((i + 1, j)\) 即可!
第 2 个要求相当于,整个过程里,不能碰到直线 \(y = x - 2\)。类比卡特兰数的推导方法,考虑用总数减去不合法的路径数。
- 总数即从 \((i + 1, j)\) 走到 \((n, n)\) 的路径数,显然是 \({n - (i + 1) + n - j\choose n - (i + 1 )} = {2n-i-j-1\choose n - i - 1}\)。
- 不合法即碰到了直线 \(y = x - 2\)。我们在它第一次碰到时,将路径关于 \(y = x - 2\) 对称。那么【不合法的路径】和【从 \((i + 1, j)\) 走到 \((n + 2, n - 2)\) 的路径】形成了一一映射。所以不合法的路径数等于【从 \((i + 1, j)\) 走到 \((n + 2, n - 2)\) 的路径数】,即 \({(n + 2) - (i + 1) + (n - 2) - j\choose (n + 2) - (i + 1)} = {2n-i-j-1\choose n - i + 1}\)。
综上所述,\(\mathrm{dp}(i, j) = {2n - i - j - 1\choose n - i - 1} - {2n - i - j - 1\choose n - i + 1}\)。按之前的方法,直接统计答案即可。
注意,如果 \(q\) 的前 \(i\) 位已经存在不合法的情况(不符合“第 \(i\) 位要么填一个 \(> \mathrm{mx}_{i-1}\) 的数,要么填 \(< \mathrm{mx}_{i-1}\) 的最小的数”这条规则),要及时 \(\texttt{break}\)。
时间复杂度 \(\mathcal{O}(n)\)。
参考代码
实际提交时请使用读入优化,详见本博客公告。
// problem: LOJ2719
#include <bits/stdc++.h>
using namespace std;
#define mk make_pair
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
template<typename T> inline void ckmax(T& x, T y) { x = (y > x ? y : x); }
template<typename T> inline void ckmin(T& x, T y) { x = (y < x ? y : x); }
const int MAXN = 6e5, MOD = 998244353;
inline int mod1(int x) { return x < MOD ? x : x - MOD; }
inline int mod2(int x) { return x < 0 ? x + MOD : x; }
inline void add(int &x, int y) { x = mod1(x + y); }
inline void sub(int &x, int y) { x = mod2(x - y); }
inline int pow_mod(int x, int i) {
int y = 1;
while (i) {
if (i & 1) y = (ll)y * x % MOD;
x = (ll)x * x % MOD;
i >>= 1;
}
return y;
}
int fac[MAXN * 2 + 5], ifac[MAXN * 2 + 5];
inline int comb(int n, int k) {
if (n < 0 || k < 0 || n < k) return 0;
return (ll)fac[n] * ifac[k] % MOD * ifac[n - k] % MOD;
}
void facinit(int lim = MAXN) {
fac[0] = 1;
for (int i = 1; i <= lim; ++i) fac[i] = (ll)fac[i - 1] * i % MOD;
ifac[lim] = pow_mod(fac[lim], MOD - 2);
for (int i = lim - 1; i >= 0; --i) ifac[i] = (ll)ifac[i + 1] * (i + 1) % MOD;
}
int n, a[MAXN + 5];
bool vis[MAXN + 5];
inline int f(int i,int j){
if(i > j) return 0;
if (i == n && j == n) return 1;
return mod2(comb(n + n - i - j - 1, n - i - 1) - comb(n + n - i - j - 1, n - i + 1));
}
void solve_case() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
vis[i] = 0;
}
int ans = 0;
for (int i = 1, mx = 0, pos = 1; i <= n; ++i) {
// 枚举从第 i 个位置起, 新序列大于原序列
mx = max(mx, a[i]);
add(ans, f(i - 1, mx + 1));
// pos 是最小的没有填过的值
if (a[i] < mx && a[i] != pos)
break; // 已经不合法了!
vis[a[i]] = 1;
while (vis[pos]) ++pos;
}
cout << ans << endl;
}
int main() {
freopen("inverse.in","r",stdin);
freopen("inverse.out","w",stdout);
facinit(MAXN * 2);
int T; cin >> T; while (T--) {
solve_case();
}
return 0;
}
一道类似的题目
ARC068D Solitaire(加强版)
该加强版见于六校联考,目前不公开,无法提交。
题目大意:
给定正整数 \(n\),和一个初始为空的双端队列。将 \(1,2,\dots,n\) 顺次插入该双端队列的任何一端。再以任意顺序从两端弹出数形成一个长为 \(n\) 的排列。对于一个排列,若存在一种操作方式得到它,则称它是好的。
现在有 \(q\) 次询问,每次给定 \(n, m(1\le m\le n)\),请求出长度为 \(n\) 且第 \(m\) 项为 \(1\) 的好的排列的个数,对 \(998244853\) 取模。
数据范围:\(1\leq n\le 3\times 10^6\),\(1\leq q\le 5\times 10^5\)。
称通过把 \(1\dots n\) 依次从两侧加入得到的排列为一个“双端队列”。发现一个排列是双端队列当且仅当其从开头到 \(1\) 递减,从 \(1\) 到结尾递增。
按照题目的定义,一个好的排列,指它能够通过从一个双端队列两侧弹出数字得到。发现一个排列是好的,当且仅当它能被拆分为两个子序列 \(A, B\),且 \(A + \mathrm{reverse}(B)\) 是一个双端队列。这里 \(A\) 就代表从左边弹出的数,\(B\) 就代表从右边弹出的数。
不妨假设 \(1\) 是从左边弹出的。如果它是从右边弹出的,则把双端队列反转一下即可。换句话说,我们通过 \(1\) 被弹出的方向,来定义“左”和“右”。
那么 \(A\) 应该先递减,减到 \(1\),然后递增;\(B\) 应该一直递减。且 \(B\) 里的所有数,应该都大于 \(A\) 中在 \(1\) 后面的数。
我们先假设,\(1\) 是 \(A\) 里的最后一个数。也就是结果序列的 \(m + 1\dots n\) 位置全部划给 \(B\)。假设此时 \(A\), \(B\) 已经确定。然后枚举一个 \(k\in[0, n - m]\), 把 \(B\) 里前 \(k\) 小的数还给 \(A\)。相当于本来 \(B\) 里前 \(n - m\) 小的数字,是按从大到小填在 \(m + 1\dots n\) 这些位置上,现在我们要从中选出 \(k\) 个位置,把前 \(k\) 小的数从小到大填在这 \(k\) 个位置上,其他数从大到小填在剩下的位置上。这么做的方案数是:
其中,\({n - m\choose k}\) 表示选出还给 \(A\) 的这 \(k\) 个位置。减去 \({n - m - 1\choose k - 1}\),是如果位置 \(n\) 出现在这 \(k\) 个位置当中,那么同样的排列在 \(k - 1\) 时已经被统计过了(也就是说,如果位置 \(n\) 恰好填第 \(k\) 小的数,则把它划分给 \(A\) 或划分给 \(B\) 都是合法的,所以这种排列会被计算两次,要减掉)。
注:后来读了题解,发现一种更简单的理解方法。考虑 \(1\) 被从双端队列里弹出后,队列里剩余 \(n - m\) 个数。每个数都可以选择从左边弹出或从右边弹出,所以方案数是 \(2^{n - m - 1}\)。
现在我们已经会处理后半部分了。接下来只需要考虑【\(1\) 是 \(A\) 里的最后一个数】的划分方案,把这个方案乘以 \(2^{n - m - 1}\) 就是答案(注意特判 \(m = n\) 时不用乘)。问题转化为:求一个排列,满足它能被划分为两个单调减序列,且位置 \(m\) 上是 \(1\)。
定义一个排列是优美的,当且仅当它能被划分为两个单调减序列。根据 \(\text{Dilworth}\) 定理,一个排列是优美的,当且仅当它不存在长度 \(\geq 3\) 的上升子序列。
对排列 \(p\),定义 \(p^{-1}\) 也是一个排列,满足 \(p^{-1}_{p_i} = i\),也就是把原排列里的“数值”和“位置”互换了。发现一个排列 \(p\) 是优美的,等价于 \(p^{-1}\) 是优美的。
所以问题转化为,求位置 \(1\) 上是 \(m\) 的、不存在长度 \(\geq 3\) 的上升子序列的,排列数量。
这个问题几乎就是 NOI2018 冒泡排序,只不过把下降改成了上升。方法是一样的:通过 DP 和卡特兰数,可以推出,答案就是从 \((2, m)\) 走到 \((n, 1)\)(每步只能向右或向下),且不碰到直线 \(y = -x + n + 3\) 的路径数,是 \({n - 2 + m - 1\choose n - 2} - {n + m - 3\choose n}\)。推导过程留给读者自行完成。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号