正睿2019CSP冲刺 选做
更新中...
day1-序列
枚举最终序列第一个位置上数的奇偶性,这样最终序列里每个位置上数的奇偶性就都确定了。特别地,如果原序列长度为奇数,则第一个位置上数的奇偶性不用枚举,看哪种数出现的多就是哪种数。
确定了最终序列里每个位置数的奇偶性后,发现奇数和偶数的移动方式互不影响,可以分别计算代价。
问题转化为,把原序列里一些位置上的数,移动到最终序列的一些位置上,使得移动距离之和最小。在此基础上,使得最终序列的字典序最小。
如果不考虑字典序,那么一种一定合法的移动方案是:让所有数相对位置不变。即:从左往右数起,第一个要移动的数,移到第一个坑;第二个数移到第二个坑,以此类推。显然,这样做移动距离之和是最小的。我们称这种方案为初始移动方案。当然,可能存在移动距离和它相等的方案,但是字典序更小。于是我们要问:什么样的移动方式,能使移动距离和初始移动方案一样小?
我们把原序列里要移动的数分为三类:
- 在初始移动方案中向左移的数。即:它在最终序列里的位置,比在原序列里的位置小。
- 在初始移动方案中位置不变的数。
- 在初始移动方案中向右移的数。即:它在最终序列里的位置,比在原序列里的位置大。
我们发现,任意一个移动方案,它的移动距离和初始移动方案一样小,当且仅当在这种移动方案下,每个要移动的数的类别和初始移动方案下相同。
于是,我们可以把所有要移动的数,按在初始移动方案下的类别分段,每一段内的数类别相同。那么根据上面的分析,不同的段之间不会有移动,也就是说,每一段是独立的。
考虑在当前段内,如何在让移动距离不变的前提下,使字典序最小。如果当前段里是第二类数,显然每个数的位置都不能改变,直接按初始移动方案摆放即可。如果当前段里是第一类数,我们将它们按数值从大到小排序,依次把每个数都尽可能靠后放(前提是它必须是“左移”的)。如果当前段里是第二类数,我们将它们按数值从小到大排序,依次把每个数都尽可能靠前放(前提是它必须是“右移”的)。具体实现中,我们可以用set来维护尚未占用的位置,二分出当前数前面/后面第一个未被占用的位置,并从set里删除即可。
时间复杂度\(O(n\log n)\)。
参考代码(片段):
const int MAXN=1e5;
int n,a[MAXN+5],vals[MAXN+5],flag[MAXN+5],res1[MAXN+5],res2[MAXN+5];
ll solve(int st_odd,int* res){
static int pos[MAXN+5];
for(int i=1,odd=st_odd,even=3-st_odd;i<=n;++i){
pos[a[i]]=i;//pos[x]: x这个值在原序列里的出现位置
if(vals[a[i]]&1){
res[odd]=a[i];
odd+=2;
}
else{
res[even]=a[i];
even+=2;
}
}
#define type(i) ((pos[res[i]]<(i))?1:(pos[res[i]]==(i)?0:-1))
for(int cur=1;cur<=2;++cur){//当前要填:奇数位/偶数位
for(int i=cur;i<=n;i+=2){
int j=i;
set<int>s;
vector<int>v;
s.insert(i);
v.pb(res[i]);
while(j+2<=n&&type(j+2)==type(i)){
j+=2;
s.insert(j);
v.pb(res[j]);
}
sort(v.begin(),v.end());
if(type(i)==1){
//原 --右移--> 新
for(int k=0;k<SZ(v);++k){
int p=*s.lob(pos[v[k]]);
s.erase(p);
res[p]=v[k];
}
}
else if(type(i)==-1){
//原 --左移--> 新
for(int k=SZ(v)-1;k>=0;--k){
int p=*(--s.upb(pos[v[k]]));
s.erase(p);
res[p]=v[k];
}
}
i=j;
}
}
#undef type
ll ans=0;
for(int i=1;i<=n;++i)ans+=abs(i-pos[res[i]]);
return ans;
}
int main() {
cin>>n;
int cnt_odd=0;
for(int i=1;i<=n;++i)cin>>a[i],vals[i]=a[i],cnt_odd+=a[i]&1;
sort(vals+1,vals+n+1);
for(int i=1;i<=n;++i){
a[i]=lob(vals+1,vals+n+1,a[i])-vals;
a[i]+=(flag[a[i]]++);
}
if(n&1){
solve(cnt_odd>n-cnt_odd?1:2,res1);
for(int i=1;i<=n;++i)cout<<vals[res1[i]]<<" \n"[i==n];
}
else{
ll v1=solve(1,res1);
ll v2=solve(2,res2);
if(v1<v2||(v1==v2&&res1[1]<res2[1])){
for(int i=1;i<=n;++i)cout<<vals[res1[i]]<<" \n"[i==n];
}
else{
for(int i=1;i<=n;++i)cout<<vals[res2[i]]<<" \n"[i==n];
}
}
return 0;
}
day1-灯泡
建出一张图。如果第\(i\)个灯泡和第\(i+1\)个灯泡同时亮着,我们就在\(i\)和\(i+1\)两个点之间连一条边。则极长亮灯区间数(答案)就是这张图里的连通块数。
显然,每个连通块都是一条链。而链是特殊的树,它具有树的性质:一棵树的 点数-边数\(=1\),一个森林的连通块数=总点数-总边数。问题转化为,对亮着的点,分别维护它们的总点数和总边数。
总点数是很好维护的。考虑如何维护总边数。
设置一个阈值\(B\)。
对于每种颜色,我们根据它在序列里出现的次数,分为次数\(\leq B\)的颜色(小颜色)和次数\(>B\)的颜色(大颜色)。
如果修改小颜色,我们直接暴力枚举这种颜色的每一次出现,根据它两边的点的状态,更新总边数。复杂度\(O(B)\)。
如果修改大颜色,则与这个大颜色的点相连的边有两种:
- 和其他大颜色相连。其他大颜色的数量只有\(\frac{n}{B}\)个,暴力枚举每个大颜色,更新总边数。
- 和小颜色相连。我们对每个大颜色,维护一个标记。在修改小颜色时,枚举所有与它相连的大颜色,更新这种大颜色的标记,表示如果这种大颜色被修改,会对总边数造成多大的影响。这样,在修改大颜色时,这部分的贡献就等于该颜色的标记。
时间复杂度\(O(q(B+\frac{n}{B}))\)。
参考代码:
const int MAXN=2e5,B=500;
int n,q,m,a[MAXN+5],app[MAXN+5],id[MAXN+5],cnt[B+5][B+5],mem[B+5],E,V;
bool st[MAXN+5];
vector<int>G[MAXN+5],big;
int main() {
cin>>n>>q>>m;
for(int i=1;i<=n;++i){
cin>>a[i];
if(a[i]==a[i-1]){i--,n--;continue;}
app[a[i]]++;
}
for(int i=1;i<=n;++i){
if(i!=1)G[a[i]].pb(a[i-1]);
if(i!=n)G[a[i]].pb(a[i+1]);
}
for(int i=1;i<=m;++i){
if((int)G[i].size()>B){
id[i]=big.size();
big.pb(i);
}
}
for(int i=0;i<(int)big.size();++i){
int u=big[i];
for(int j=0;j<(int)G[u].size();++j){
if((int)G[G[u][j]].size()>B){
cnt[id[u]][id[G[u][j]]]++;
}
}
}
while(q--){
cin>>u;
if(st[u])V-=app[u];else V+=app[u];
if((int)G[u].size()<=B){
for(int i=0;i<(int)G[u].size();++i){
int v=G[u][i];
if(st[u]&&st[v])E--;
else if(!st[u]&&st[v])E++;
if((int)G[v].size()>B){
if(st[u])mem[id[v]]--;
else mem[id[v]]++;
}
}
}else{
if(st[u])E-=mem[id[u]];else E+=mem[id[u]];
for(int i=0;i<(int)big.size();++i){
int v=big[i];
if(v==u)continue;
if(st[u]&&st[v])E-=cnt[id[u]][id[v]];
else if(!st[u]&&st[v])E+=cnt[id[u]][id[v]];
}
}
st[u]^=1;
cout<<V-E<<endl;
}
return 0;
}
day1-比赛
我们定义,\(f(n,k)\)表示\(n\)个人中,存在一个大小为\(k\)的合法集合的概率。可以形式化地定义为:\(f(n,k)=\sum_{|s|=k}\prod_{i\in s}p^{\operatorname{cntGreater}(i)}(1-p)^{\operatorname{cntLess}(i)}\)。其中\(\operatorname{cntGreater}(i)\)表示不在集合里的选手中编号大于\(i\)的选手数量,\(\operatorname{cntLess}(i)\)表示不在集合里的选手中编号小于\(i\)的选手数量。
我们可以DP求\(f\)。考虑转移。考虑\(f(n+1,k)\),我们可以从\(f(n,k)\)和\(f(n,k-1)\)两个地方转移,分别对应了第\(n+1\)个人 不在/在 颁奖集合里。如果\(n+1\)不在颁奖集合里,那么他要输给前面的\(k\)个在颁奖集合里的人;如果\(n+1\)在颁奖集合里,那么他要赢得前面的\(n-k+1\)个不在颁奖集合里的人。于是可以得到对应的转移系数:
大力实现这个DP,时间复杂度是\(O(n^2)\)的。考虑优化。
我们思考另一种转移。我们还是让\(f(n+1,k)\)从\(f(n,k)\)和\(f(n,k-1)\)转移过来,但不是新增一个编号最大的人,而是新增一个编号最小的人!即,之前我们让\(n+1\)做出转移,现在我们让\(1\)来做转移。如果\(1\)不在颁奖集合里,那么他要输给后面的\(k\)个在颁奖集合里的人;如果\(1\)在颁奖集合里,那么他要赢得后面的\(n-k+1\)个不在颁奖集合里的人。于是可以写出另一种转移式:
把\((1)\), \((2)\)两个式子联立。可得:
移项得:
当\(p\neq \frac{1}{2}\)时,我们就相当于得到了对于同一个\(n\),不同的\(k\),\(f(n,k)\)的递推式。直接\(O(n)\)递推一遍,就能求出所有\(k\)的答案了。
当\(p=\frac{1}{2}\)时,上述的式子不再能用于递推。我们要特判这种情况,并对这种情况单独想一个解法(有点二合一的意思)。幸运的是,这种情况的解法其实非常简单。因为所有人,无论编号,获胜的概率都一样。对于同一个\(k\),我们选出任意\(k\)个人作为颁奖集合都是等价的。所以直接用选出一个合法集合的概率,乘以\(n\choose k\)即可。即:
时间复杂度\(O(n)\)或\(O(n\log n)\)。其中\(\log\)是如果你不做预处理,直接一边递推一边快速幂带来的。
参考代码(片段):
const int MAXN=1e6,MOD=998244353;
inline int pow_mod(int x,int i){
int y=1;
while(i){
if(i&1)y=(ll)y*x%MOD;
x=(ll)x*x%MOD;
i>>=1;
}
return y;
}
inline int mod(int x){return x<MOD?(x<0?x+MOD:x):x-MOD;}
int n,p,q,f[MAXN+5],F[MAXN+5],fac[MAXN+5],invf[MAXN+5],ans;
int main() {
cin>>n>>p>>q;
p=(ll)p*pow_mod(q,MOD-2)%MOD;q=mod(1-p);
if(p==q){
fac[0]=1;for(int i=1;i<=n;++i)fac[i]=(ll)fac[i-1]*i%MOD;
invf[n]=pow_mod(fac[n],MOD-2);
for(int i=n-1;i>=0;--i)invf[i]=(ll)invf[i+1]*(i+1)%MOD;
assert(invf[0]==1);
f[1]=1;
for(int i=1;i<n;++i){
ans=mod(ans+(ll)f[i]*fac[n]%MOD*invf[i]%MOD*invf[n-i]%MOD*pow_mod(pow_mod(2,(ll)i*(n-i)%(MOD-1)),MOD-2)%MOD);
f[i+1]=mod((ll)f[i]*f[i]%MOD+2);
}
cout<<ans<<endl;
return 0;
}
F[1]=(ll)mod(pow_mod(p,n)-pow_mod(q,n))*pow_mod(mod(p-q),MOD-2)%MOD;
f[1]=1;ans=F[1];
for(int i=2;i<n;++i){
f[i]=mod((ll)f[i-1]*f[i-1]%MOD+2);
F[i]=(ll)F[i-1]*mod(pow_mod(p,n-i+1)-pow_mod(q,n-i+1))%MOD*pow_mod(mod(pow_mod(p,i)-pow_mod(q,i)),MOD-2)%MOD;
ans=mod(ans+(ll)f[i]*F[i]%MOD);
}
cout<<ans<<endl;
return 0;
}//4 2 6
day2-石子
第一堆石子被取走的期望时间,等于在第一堆石子之前被取走的堆数的期望,加\(1\)。
根据期望的线性性,第一堆石子之前被取走的堆数的期望,可以拆成每一堆石子的期望之和。而每一堆石子对总堆数的贡献要么是\(0\),要么是\(1\),因此它的期望在数值上就等于它在第一堆之前被取走的概率。我们设第\(i\)堆石子(\(i\geq2\))在第一堆之前被取走的概率为\(P_i\)。则答案等于\(\sum_{i=2}^{n}P_i+1\)。
第\(i\)堆石子在第一堆石子之前被取走,这个事件和其它石子被取的情况是无关的。也就是说,只要考虑这两堆的情况。所以,\(P_i=\frac{a_i}{a_1+a_i}\)。
答案就是\(\sum_{i=2}^{n}\frac{a_i}{a_1+a_i}+1\),直接计算即可。
时间复杂度\(O(n)\)。
参考代码(片段):
int n;
long double a[100005];
int main() {
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i];
long double ans=0;
for(int i=2;i<=n;++i)ans+=a[i]/(a[i]+a[1]);
ans+=1;
cout<<setiosflags(ios::fixed)<<setprecision(233)<<ans<<endl;
return 0;
}
day2-内存
暴力的做法是,我们枚举\(x\in[0,m)\),用当前\(x\)能取到的最优解\(f(x)\)更新答案。
对于给定的\(x\),如何求\(f(x)\)?我们可以二分答案\(\text{mid}\),贪心地从左往右扫,每当当前段的和\(>\text{mid}\),就令最后一个数自成一个新的段。若总段数\(\leq k\),说明当前\(\text{mid}\)可行,否则\(\text{mid}\)需要变大。
上述做法总时间复杂度\(O(mn\log n)\)。
考虑优化。我们按随机顺序访问所有\(x\)。维护一个全局的最优答案\(\text{ans}\)。访问某个\(x\)时,先令\(\text{mid}=\text{ans}\),做一次check,如果check未通过,说明当前\(x\)的\(f(x)\)一定大于\(\text{ans}\),可以直接跳到下一个\(x\)。否则我们和前面一样老老实实二分\(f(x)\),更新答案。
考虑这么做的时间复杂度。首先,因为每个\(x\)会先check一次\(\text{mid}=\text{ans}\),所以时间复杂度至少是\(O(mn)\)。如果这第一次check就未通过,我们就不需要继续进行二分了。考虑第一次check通过的概率,相当于当前\(x\)的\(f(x)\),是我们访问过的所有\(x\)的前缀最小值。我们以随机顺序访问\(x\),第\(i\)个\(f(x)\)是前缀最小值的概率为\(\frac{1}{i}\),所以每个\(x\)第一次check能通过的期望次数之和是\(O(\sum_{i\leq m}\frac{1}{i})=O(\ln m)\)次。因此,总时间复杂度为\(O(nm+\ln m\cdot n\log n)\)。
参考代码(片段):
int n,m,K,a[100005],X[1005];
inline int mod(int x){return x<m?x:x-m;}
bool check(int mid,int x){
int cur=0,cnt=0,ok=1;
for(int i=1;i<=n;++i){
int t=mod(a[i]+x);
if(t>mid){ok=0;break;}
if(cur+t>mid){
++cnt;
cur=0;
}
cur+=t;
}
if(cur)++cnt;
if(cnt>K||!ok)return 0;
return 1;
}
int main() {
srand((ull)time(0)^(ull)(new char));
cin>>n>>m>>K;
for(int i=1;i<=n;++i)cin>>a[i];
for(int i=1;i<=m;++i)X[i]=i-1;
random_shuffle(X+1,X+m+1);
int ans=n*m;
for(int t=1;t<=m;++t){
int x=X[t];
if(!check(ans-1,x))continue;
int l=0,r=ans;
while(l<r){
int mid=(l+r)>>1;
if(check(mid,x))r=mid;
else l=mid+1;
}
//cout<<l<<endl;
ans=min(ans,l);
}
cout<<ans<<endl;
return 0;
}
day2-子集
首先,选出来的数一定都是\(n\)的约数,否则\(\operatorname{lcm}\)不会等于\(n\)。具体来说:如果把\(n\)分解质因数后\(n=p_1^{c_1}p_2^{c_2}\cdots p_{k}^{c_k}\),则对于每个质因数\(p_i\),集合中一定有至少一个数中\(p_i\)的次数为\(c_i\),也一定有至少一个数中\(p_i\)的次数为\(0\)。
考虑容斥原理。如果\(n\)只有一个质因数,即\(n=p_1^{c_1}\),则用总方案数(情况二),减去不存在\(p_1\)的次数为\(c_1\)的方案数(情况二),减去不存在\(p_1\)的次数为\(0\)的方案数(情况三),再加上两者都不存在的方案数(情况四)。
当\(n\)有多个质因子时,不妨记\(n\)有\(k(n)\)个质因子。我们在\(O(4^{k(n)})\)的时间里枚举每个质因子属于那种情况,乘上对应的容斥系数,然后加入答案中。但是这个时间复杂度不足以通过本题。考虑优化。
对于一个在\(n\)中次数为\(c_i\)的质因数,如果它是情况一,那么它有\(c_i+1\)种选择。如果它是情况二或者情况三,那么它有\(c_i\)种选择。如果它是情况四,那么它有\(c_i-1\)种选择。注意到,情况二和情况三的方案数是相同的!所以我们不枚举是四种情况中的哪一种,而是枚举是三种方案数中的哪一种。如果方案数是\(c_i+1\)或\(c_i-1\),则容斥系数不变,否则容斥系数乘以\(-2\)。时间复杂度\(O(3^{k(n)}k(n))\),可以通过本题。
以上就是本题的主要思路。还有一个小问题:如何对\(n\)分解质因数呢?本题中\(n\)高达\(10^{18}\),传统的\(O(\sqrt{n})\)方法无法胜任。当然,如果你会PollardRho算法,那么你可以跳过此部分。但是注意到我们其实只需要知道每个质因子的次数,而不用知道每个质因子具体是什么。所以不需要使用PollardRho算法。我们先把\(n\)中\(\leq\sqrt[3]{n}\)的质因子全部筛掉。剩下的数只有几种情况:
- 剩下的数是\(1\)。也就是说\(n\)没有大于\(\sqrt[3]{n}\)的质因子。
- 剩下的数是质数。这个大质数判定可以用MillerRabin算法实现。
- 剩下的数是完全平方数,那么它一定是某个质数的平方。
- 如果不是以上三种情况,说明剩下的数是两个次数均为\(1\)的不同质因子相乘。
这样,总时间复杂度就是\(O(\sqrt[3]{n}+\log n+3^{k(n)})\)。
参考代码(片段):
const ll MOD=998244353LL;
inline ll mul(ll x,ll y,ll M=MOD){return (__int128)x*y%M;}//迫真快速乘
inline ll pow_mod(ll x,ll i,ll M=MOD){
ll y=1;
while(i) {
if(i&1) y=mul(y,x,M);
x=mul(x,x,M);
i>>=1;
}
return y;
}
namespace MR{
inline bool check(ll x,int a,ll d){
if(!(x&1LL))return false;/*x!=2 且 x为偶数*/
while(!(d&1LL))d>>=1;
ll t=::pow_mod(a,d,x);
if(t==1 || t==x-1)return true;
while(t!=1 && d!=x-1){
t=::mul(t,t,x);
d<<=1;
if(t==x-1)return true;
}
return false;
}
const int a[10]={2,3,5,7,11,13,17,19,23,29};
inline bool is_prime(ll x){
if(x==1)return false;
for(int i=0;i<10;++i)if(x==a[i])return true;
for(int i=0;i<10;++i){
if(!check(x,a[i],x-1))return false;
}
return true;
}
}//namespace MR
bool is_sqr(ll x){ll t=sqrt(x);return t*t==x;}
int a[100],cnt,pw[100];
int main() {
ll n;cin>>n;
for(ll i=2;i*i<=n&&i<=1000000;++i){
int e=0;
while(n%i==0)e++,n/=i;
if(e)a[++cnt]=e;
}
if(n!=1){
if(MR::is_prime(n))a[++cnt]=1;
else if(is_sqr(n))a[++cnt]=2;
else a[++cnt]=1,a[++cnt]=1;
}
pw[0]=1;for(int i=1;i<=cnt;++i)pw[i]=pw[i-1]*3;
int ans=0;
for(int i=0;i<pw[cnt];++i){
ll x=1;int y=1;
for(int j=1;j<=cnt;++j){
int e=i/pw[j-1]%3;
x=x*(a[j]+1-e);
if(e==1)y*=-2;
}
if(y<0)y+=MOD;x%=(MOD-1);
ans=(ans+y*(pow_mod(2,x)-1)%MOD)%MOD;
}
cout<<ans<<endl;
return 0;
}
day4-路径
考虑在dfs整棵树的过程中顺便构造出哈密尔顿回路。
如果树是一条链,我们可以用如下方法构造(图片来自戴言老师的题解):

当树不是一条链时,我们用类似的方法构造。题解给出了这一构造方法的极具概括性的描述:
对于深度为奇数的节点,我们先输出它,再遍历它的整个子树;对于深度为偶数的节点,我们先遍历它的整个子树,再输出它。
可以验证,使用这种构造方法,输出中连续的两个节点,在树上的距离不会超过\(3\)。下图是距离等于\(3\)的一种示例,其中3号边(标为蓝色)距离为\(3\)。显然,这是能达到的最大距离了。

时间复杂度\(O(n)\)。
参考代码(片段):
const int MAXN=3e5;
struct EDGE{int nxt,to;}edge[MAXN*2+5];
int n,head[MAXN+5],tot,ans[MAXN+5],cnt;
inline void add_edge(int u,int v){edge[++tot].nxt=head[u];edge[tot].to=v;head[u]=tot;}
void dfs(int u,bool fir,int fa){
if(fir)ans[++cnt]=u;
for(int i=head[u];i;i=edge[i].nxt)if(edge[i].to!=fa)dfs(edge[i].to,fir^1,u);
if(!fir)ans[++cnt]=u;
}
int main() {
cin>>n;
for(int i=1,u,v;i<n;++i)cin>>u>>v,add_edge(u,v),add_edge(v,u);
cout<<"Yes"<<endl;
dfs(1,1,0);for(int i=1;i<=n;++i)cout<<ans[i]<<" \n"[i==n];
return 0;
}
day4-魔法
对所有\(T\)串,建出AC自动机。对自动机上每个节点,记录一个值\(len[u]\),表示匹配到节点\(u\)的\(T\)串中长度最小的串长度为多少。这里“匹配到节点\(u\)”,指的是该\(T\)串是根节点到\(u\)的路径所组成的串的一个后缀。特别地,如果没有串匹配到节点\(u\),则令\(len[u]=\inf\)。
对\(S\)求出一个数组\(lim[1\dots n+1]\)。\(lim[i]\)表示\(S\)的\(1\dots i-1\)位中,最后一个被删掉的位置,不能早于\(lim[i]\)。换句话说,\(lim[i]\sim i-1\)这段区间内,至少有一个位置需要被删除。特别地,如果对位置\(i\)没有限制,我们令\(lim[i]=0\),相当于默认第\(0\)个位置是已经被删除的。如何求\(lim\)数组?可以让\(S\)在AC自动机上走一遍,设\(S\)的前\(i\)位走到AC自动机上的节点\(u_i\),则:\(lim[i+1]=\max(0,i-len[u_i]+1)\)。
当然,由于良心的出题人设置了\(m\leq10\)的条件,如果你不会AC自动机,求\(lim\)数组的过程也可以通过对每个\(T\)分别做KMP来实现。这里不再赘述。
求出\(lim\)数组后,我们考虑DP。设\(dp[i][j]\)表示考虑了前\(i\)位,最后一个被删除的位置为\(j\)的最小代价。转移时,分三种情况:
- 对于\(lim[i]\leq j\leq i-1\),\(dp[i][j]=dp[i-1][j]\)。
- 对于\(j=i\),\(dp[i][j]=\min_{k=lim[i]}^{i-1}dp[i-1][k]+a[i]\)。
- 对于其他的\(j\),\(dp[i][j]=\inf\)。
发现,从\(i-1\)到\(i\)的转移,对DP数组第二维的修改,相当于把一段前缀(\([0,lim[i]-1]\))赋值为\(\inf\),再对位置\(i\)做一个单点修改。这可以用线段树实现。
时间复杂度\(O(\sum|T|+n\log n)\)。如果前半部分用KMP实现,则复杂度变为\(O(\sum_{i=1}^{m}(|S|+|T_i|)+n\log n)\)。
参考代码(片段):
const int MAXN=2e5;
int n,m,a[MAXN+5],lim[MAXN+5];
char s[MAXN+5],t[MAXN+5];
namespace AC{
const int MAXN=2e6;
int tot,tr[MAXN+5][26],len[MAXN+5],fa[MAXN+5];
void insert_string(char* s,int n){
int u=1;
for(int i=1;i<=n;++i){
if(!tr[u][s[i]-'a'])tr[u][s[i]-'a']=++tot,len[tot]=(::n)+1;
u=tr[u][s[i]-'a'];
}
len[u]=min(len[u],n);
}
void build(){
for(int i=0;i<26;++i)tr[0][i]=1;
queue<int>q;q.push(1);
while(!q.empty()){
int u=q.front();q.pop();
len[u]=min(len[u],len[fa[u]]);
for(int i=0;i<26;++i){
if(tr[u][i]){
fa[tr[u][i]]=tr[fa[u]][i];
q.push(tr[u][i]);
}
else tr[u][i]=tr[fa[u]][i];
}
}
}
void init(){
tot=1;
len[0]=len[1]=(::n)+1;
}
}//namespace AC
const int INF=1e9;
struct SegmentTree{
int val[(MAXN+1)*4+5];
bool tag[(MAXN+1)*4+5];
void push_up(int p){
val[p]=min(val[p<<1],val[p<<1|1]);
}
void push_down(int p){
if(tag[p]){
val[p<<1]=INF;
tag[p<<1]=1;
val[p<<1|1]=INF;
tag[p<<1|1]=1;
tag[p]=0;
}
}
void build(int p,int l,int r){
if(l==r){
if(l==0)val[p]=0;
else val[p]=INF;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
push_up(p);
}
void setINF(int p,int l,int r,int ql,int qr){
if(ql<=l&&qr>=r){
val[p]=INF;
tag[p]=1;
return;
}
push_down(p);
int mid=(l+r)>>1;
if(ql<=mid)setINF(p<<1,l,mid,ql,qr);
if(qr>mid)setINF(p<<1|1,mid+1,r,ql,qr);
push_up(p);
}
void point_change(int p,int l,int r,int pos,int v){
if(l==r){
val[p]=v;
return;
}
push_down(p);
int mid=(l+r)>>1;
if(pos<=mid)point_change(p<<1,l,mid,pos,v);
else point_change(p<<1|1,mid+1,r,pos,v);
push_up(p);
}
SegmentTree(){}
}T;
int main() {
cin>>n>>m;
cin>>(s+1);
for(int i=1;i<=n;++i)cin>>a[i];
AC::init();
for(int i=1;i<=m;++i){
cin>>(t+1);
int len=strlen(t+1);
AC::insert_string(t,len);
}
AC::build();
int u=1;
for(int i=1;i<=n;++i){
u=AC::tr[u][s[i]-'a'];
lim[i+1]=max(0,i-AC::len[u]+1);
}
//for(int i=1;i<=n+1;++i)cout<<lim[i]<<" ";cout<<endl;
/*
static int f[5005][5005];
memset(f,0x3f,sizeof(f));
f[0][0]=0;
for(int i=1;i<=n;++i){
for(int j=lim[i];j<i;++j){
f[i][j]=f[i-1][j];
f[i][i]=min(f[i][i],f[i-1][j]+a[i]);
}
}
int ans=INF;
for(int i=lim[n+1];i<=n;++i)ans=min(ans,f[n][i]);
cout<<ans<<endl;
*/
T.build(1,0,n);
for(int i=1;i<=n+1;++i){
if(lim[i]){
T.setINF(1,0,n,0,lim[i]-1);
}
if(i==n+1)break;
T.point_change(1,0,n,i,T.val[1]+a[i]);
}
cout<<T.val[1]<<endl;
return 0;
}
相关题目推荐:
CF1327F AND Segments 记录每个位置最早能转移的点\(lim[i]\),并用线段树优化二维DP,这两个套路都和本题很像。我的题解
day4-交集
容易发现\(u\), \(v\)是两个独立的问题,即:我们只需要在\(u\)处选\(k\)个点,在\(v\)处选\(k\)个点,然后把方案数相乘即可。具体地讲,这里在\(u\)处选\(k\)个点,指的是:令\(u\)为根,在树上任选\(k\)个点,使他们两两的LCA都为\(u\)。另外,设\(v\)在\(u\)的儿子\(w\)的子树内,则整个\(w\)子树里的点都是不能选的。当然,在具体实现时,我们不可能每次询问都真的给整棵树换个根。我们在开始询问前以\(1\)为根做好预处理,然后当需要以\(u\)为根时,我们把\(u\)连向\(fa(u)\)的边也当做\(u\)的一个儿子即可。
问题转化为:如何在树上选择\(k\)个点使他们两两的LCA都为\(u\)?显然,要使两两的LCA都是\(u\),那么在\(u\)的每个儿子的子树里就至多只能选择\(1\)个点。因为儿子只有\(\leq L\)个,我们对每个\(u\)做一个背包,就能求出,在当前\(u\)中,选择\(k\)(\(k\leq L\))个点的方案数。当然,还可以选择\(u\)本身,并且可以选多次,所以我们枚举\(u\)被选了多少次,乘一个组合数即可。
但是,注意到还有一个要求:不能取(以\(u\)为根时)\(v\)所在子树内的点。前面做的背包中并没有考虑到这个要求。
我们思考这个背包的实质,它相当于是下列生成函数\(x^k\)项前的系数:
现在要求不能取(以\(u\)为根时)\(v\)所在子树内的点,则生成函数应当变为:
容易发现,\(P_{u,v}(x)\)就是\(P_u(x)\)除掉了一个\((1+\text{size}_w\cdot x)\),其中\(w\)是\(u\)向\(v\)方向的出边。可以发现,多项式除单项式,就是背包的过程倒过来(加法变成减法)。利用预处理好的\(P_u(x)\),可以在\(O(L)\)的时间内求出\(P_{u,v}(x)\)。
时间复杂度\(O((n+q)L)\)。
参考代码(片段):
const int MOD=998244353,MAXN=1e5;
int fac[MAXN+5],invf[MAXN+5];
inline int mod(int x){return x<MOD?(x<0?x+MOD:x):x-MOD;}
inline int pow_mod(int x,int i){int y=1;while(i){if(i&1)y=(ll)y*x%MOD;x=(ll)x*x%MOD;i>>=1;}return y;}
inline int down_pow(int n,int k){return (ll)fac[n]*invf[n-k]%MOD;}//下降幂
struct EDGE{int nxt,to;}edge[MAXN*2+5];
int head[MAXN+5],tot;
inline void add_edge(int u,int v){edge[++tot].nxt=head[u];edge[tot].to=v;head[u]=tot;}
int n,an[MAXN+5][18],sz[MAXN+5],dep[MAXN+5];
void dfs(int u){
dep[u]=dep[an[u][0]]+1;
sz[u]=1;
for(int i=1;i<18;++i)an[u][i]=an[an[u][i-1]][i-1];
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(v==an[u][0])continue;
an[v][0]=u;
dfs(v);
sz[u]+=sz[v];
}
}
int lca(int u,int v){
if(dep[u]<dep[v])swap(u,v);
for(int i=17;~i;--i)if(dep[an[u][i]]>=dep[v])u=an[u][i];
if(u==v)return u;
for(int i=17;~i;--i)if(an[u][i]!=an[v][i])u=an[u][i],v=an[v][i];
return an[u][0];
}
int kth_an(int v,int k){
for(int i=17;~i;--i)if(k&(1<<i))v=an[v][i];
return v;
}
int q,L,deg[MAXN+5],dp[MAXN+5][505],f[505];
int solve(int u,int v,int k){
int w=lca(u,v);
//cout<<u<<" "<<v<<" lca:"<<w<<endl;
int ban=(u==w?kth_an(v,dep[v]-dep[w]-1):an[u][0]);
int x=(ban!=an[u][0]?sz[ban]:n-sz[u]);
f[0]=1;
int ans=1;
for(int i=1;i<deg[u]&&i<=k;++i){
f[i]=mod(dp[u][i]-(ll)f[i-1]*x%MOD);
ans=mod(ans+(ll)f[i]*down_pow(k,i)%MOD);
}
//cout<<"-- "<<ans<<endl;
return ans;
}
int main() {
cin>>n>>q>>L;
fac[0]=1;for(int i=1;i<=n;++i)fac[i]=(ll)fac[i-1]*i%MOD;
invf[n]=pow_mod(fac[n],MOD-2);
for(int i=n-1;~i;--i)invf[i]=(ll)invf[i+1]*(i+1)%MOD;assert(invf[0]==1);
for(int i=1,u,v;i<n;++i)cin>>u>>v,add_edge(u,v),add_edge(v,u);
dfs(1);
for(int i=1;i<=n;++i){
dp[i][0]=1;
for(int j=head[i];j;j=edge[j].nxt){
int x=(edge[j].to!=an[i][0]?sz[edge[j].to]:n-sz[i]);
for(int k=deg[i];~k;--k)dp[i][k+1]=mod(dp[i][k+1]+(ll)dp[i][k]*x%MOD);
++deg[i];
}
}//O(nL)
while(q--){
int u,v,k;cin>>u>>v>>k;
cout<<(ll)solve(u,v,k)*solve(v,u,k)<<endl;
}
return 0;
}
day5-染色
把白边染成黑色,相当于删除一条边。题目要求我们预先删掉一些边,使得剩下图上的边,能用题目要求的操作全部删完。
容易发现,一张图上,所有边能用题目要求的操作全部删完,当且仅当这张图中不存在环。
证明:
必要性:只要存在一个环,环上所有点度数至少为\(2\),这个环一定删不掉。
充分性:在没有环时,图是一个森林。对于一棵树,每次删掉所有连接叶子节点的边。必能通过有限次操作删完整棵树。
所以,只需要求出把原图变成一个森林,最少要删多少条边。
我们一边读入所有的边,一边用并查集维护所有点的连通性。如果当前边的两个端点\((u,v)\)已经联通,说明当前边需要删除。否则,当前边可以保留,我们用并查集把\((u,v)\)并起来。这和kruskal算法的原理是一样的。另外,显然的是,加边的顺序并不影响答案。
我们也可以更本质地考虑这个问题。设图中的连通块数为\(c\),则最后剩下的森林里的边数为\(n-c\)。故答案就是\(m-(n-c)\)。
时间复杂度\(O(n+m)\)。
参考代码(片段):
const int MAXN=1e5;
int n,m,fa[MAXN+5],ans;
int get_fa(int x){return fa[x]==x?x:(fa[x]=get_fa(fa[x]));}
int main() {
cin>>n>>m;
for(int i=1;i<=n;++i)fa[i]=i;
for(int i=1;i<=m;++i){
int u,v;cin>>u>>v;
int fau=get_fa(u),fav=get_fa(v);
if(fau==fav)ans++;
else fa[fau]=fav;
}
cout<<ans<<endl;
return 0;
}
day5-乘方
考虑二分答案,问题转化为,判断\(\bigcup_{i=1}^{k}S(n_i)\)中有多少个数\(\leq \text{mid}\)。
对\(\bigcup_{i=1}^{k}S(n_i)\)容斥。我们先计算\(S(n_1),S(n_2),\dots S(n_k)\)中\(\leq \text{mid}\)的数的数量之和,这样会重复计算;于是我们减去既在\(S(n_1)\)中,又在\(S(n_2)\)中......(同时出现在两个集合中)的\(\leq \text{mid}\)的数的数量之和;再加上同时出现在三个集合中的\(\leq \text{mid}\)的数的数量之和......。于是,我们要求:\(\text{check}(\text{mid})=\sum_{s\in [k]}(-1)^{|s|+1}\text{cnt}\left(\bigcap_{i\in s}S(n_i)\right)\)。其中\(\text{cnt}(s)\)表示集合\(s\)里\(\leq \text{mid}\)的数的数量。
容易发现,\(\bigcap_{i\in s}S(n_i)=S(\operatorname{lcm}_{i\in s}n_i)\)。
暴力的做法是直接枚举子集\(s\)。问题转化为如何对一个特定的数\(x=\operatorname{lcm}_{i\in s}n_i\),求\(\text{cnt}(S(x))\)。根据定义,\(S(x)=\{1^x,2^x,3^x,\dots\}\),显然,\(t^x<(t+1)^x\) (\(x>0\)),所以我们可以出二分最大的\(t\),满足\(t^x\leq \text{mid}\)。则\(\text{cnt}(S(x))=t\)。当然,每次二分\(t\)时,还需要做快速幂。故总复杂度为:\(O(q(\log \inf\cdot2^k\log^2 m))\),其中\(\inf\)即为最大答案,\(=10^{17}\)。无法通过subtask3。
考虑优化,发现枚举子集\(s\)后,先二分\(t\)再做快速幂是十分耗时的。我们可以利用\(\texttt{C++}\)自带的\(\texttt{pow}\)函数直接对\(\text{mid}\)开\(x\)次根(\(\texttt{pow(mid,1.0/x)}\)),再用快速幂微调一下误差即可。这样,总复杂度降为\(O(q(2^k\log^2\inf))\),可以通过subtask3。
想到用DP代替暴力枚举子集。发现一个子集的贡献,只与它的\(\operatorname{lcm}\),也就是上文中的\(x\)有关。故可以设\(dp[i][j]\)表示考虑了前\(i\)个数(\(n_1,n_2,\dots n_i\)),选出的\(\operatorname{lcm}=j\)时的容斥系数之和。发现,我们只需要考虑\(j\leq 60\)的情况,因为题目保证了答案不超过\(10^{17}\),而\(2^{60}>10^{17}\)。这样做的好处,相当于把\(\operatorname{lcm}\)相同的子集放到一起计算。于是,二分时,就不必枚举\(2^k\)个子集,只需要枚举\(60\)种\(\operatorname{lcm}\),效率大大提高。
时间复杂度:\(O(q(k\log\inf+\log^3\inf))\)。
参考代码(片段):
const ll INF=1e17;
int m,n,a[55];
ll dp[55][61];
int lcm(int x,int y){return x/__gcd(x,y)*y;}
ll pow_check(ll x,int i,ll lim=INF){
ll y=1;
while(i){
if(i&1){
if(y>lim/x)return lim+1;
y*=x;
}
if(i>1&&x>lim/x)return lim+1;
x*=x;
i>>=1;
}
return y;
// ll y=1;
// while(i--)if((double)y*x>lim)return lim+1;else y*=x;
// return y;
}
ll kaif(ll a,int b){
ll res=pow(a,1.0/b);
if(pow_check(res,b,a)<a)res++;
if(pow_check(res,b,a)>a)res--;
return res;
}
int main() {
int q;cin>>q;while(q--){
cin>>m>>n;
memset(dp,0,sizeof(dp));
dp[0][1]=-1;
for(int i=1;i<=n;++i){
cin>>a[i];
for(int j=1;j<=60;++j){
dp[i][j]+=dp[i-1][j];
int t=min(lcm(j,a[i]),60);
dp[i][t]-=dp[i-1][j];
}
}
dp[n][1]++;
//for(int i=1;i<=20;++i)cout<<dp[n][i]<<" ";cout<<endl;
ll l=1,r=INF;
while(l<r){
ll mid=(l+r)>>1,sum=0;
for(int i=1;i<=60;++i)sum+=dp[n][i]*kaif(mid,i);
//cout<<mid<<" "<<sum<<endl;
if(sum>=m)r=mid;
else l=mid+1;
}
cout<<l<<endl;
}
return 0;
}
day5-位运算
不论是\(\operatorname{AND}\), \(\operatorname{XOR}\)还是\(\operatorname{OR}\)运算,都可以直接在值域上做FWT。时间复杂度\(O(a\log a)\),其中\(a=\max_{i=1}^{n}a_i\),即值域。
但是对于\(\operatorname{AND}\)和\(\operatorname{XOR}\)运算,我们有更优秀的方法。
\(\operatorname{AND}\)运算:
从高到低按位考虑。维护一个当前可选的数的集合(可重集),初始时全部\(n\)个数都在集合中。
对于当前位,我们希望答案中它为\(1\)。
- 如果当前可选数的集合里有至少两个数这一位为\(1\),说明答案的这一位确实可以为\(1\)。因此我们一定不选这一位为\(0\)的数,把这些数从集合里删掉。然后继续考虑下一位。
- 否则,说明无论怎么选,答案的当前位都只能是\(0\)。故可选集合不变,直接考虑下一位。
当考虑完\(23\)位之后,设集合里剩余\(s\)个数。则方案数就是\(\frac{s(s-1)}{2}\)。
时间复杂度\(O(n\log a)\)。
\(\operatorname{XOR}\)运算:
这是经典的异或最大值问题。可以用01Trie解决。对所有\(n\)个数建01Trie。如果给定一个整数\(x\),问在\(n\)个数中,哪个数和\(x\)异或的结果最大。我们直接在01Trie上走一遍就知道了。
在01Trie上插入所有数后,枚举以每个\(a_i\)作为\(x\),分别计算一遍,即可求出异或的最大值,以及方案数。注意一种特殊的情况:当序列里所有数都相同时,最大值为\(0\),此时我们会把\(a_i\operatorname{XOR} a_i\)也算入方案数中,所以此时方案数要减\(n\)。
时间复杂度\(O(n\log a)\)。
参考代码(片段):
const int MAXN=1e5;
int n,q,a[MAXN+5];
namespace solver_and{
//分治
int ansv;
ll ansc;
void solve(const vector<int>& v,int dep){
if(dep==-1){
ansc=(ll)v.size()*(v.size()-1)/2;
return;
}
vector<int>newv;
for(int i=0;i<SZ(v);++i)if((v[i]>>dep)&1)newv.pb(v[i]);
if(SZ(newv)>=2){
ansv|=(1<<dep);
solve(newv,dep-1);
}
else{
solve(v,dep-1);
}
}
int main(){
vector<int>v;
for(int i=1;i<=n;++i)v.pb(a[i]);
solve(v,22);
cout<<ansv<<" "<<ansc<<endl;
return 0;
}
}//namespace solver_and
namespace solver_xor{
//01Trie
int ch[MAXN*25][2],tot,cnt[MAXN*25];
void ins(int x){
int t=1;
for(int i=22;~i;--i){
int d=((x>>i)&1);
if(!ch[t][d])ch[t][d]=++tot;
t=ch[t][d];
}
cnt[t]++;
}
pii fd(int x){
int t=1,ans=0;
for(int i=22;~i;--i){
int d=(((x>>i)&1)^1);
if(!ch[t][d])t=ch[t][d^1];
else t=ch[t][d],ans^=(1<<i);
}
return mk(ans,cnt[t]);
}
int main(){
tot=1;for(int i=1;i<=::n;++i)ins(::a[i]);
pii res=mk(0,0);
for(int i=1;i<=::n;++i){
pii cur=fd(::a[i]);
if(cur.fi>res.fi)res=cur;
else if(cur.fi==res.fi)res.se+=cur.se;
}
if(!res.fi)res.se-=n;
cout<<res.fi<<" "<<(res.se/2)<<endl;
return 0;
}
}//namespace solver_xor
namespace solver_or{
//FWT or
const int SIZE=1<<23;
ll f[SIZE],cnt[SIZE];
void fwt(ll *f,int n,int flag){
for(int i=1;i<n;i<<=1){
for(int j=0;j<n;j+=(i<<1)){
for(int k=j;k<i+j;++k){
f[i+k]+=f[k]*flag;
}
}
}
}
int main(){
for(int i=1;i<=::n;++i)f[::a[i]]++,cnt[::a[i]]++;
fwt(f,SIZE,1);
for(int i=0;i<SIZE;++i)f[i]*=f[i];
fwt(f,SIZE,-1);
for(int i=SIZE-1;~i;--i){
if(f[i]-=cnt[i]){
cout<<i<<" "<<(f[i]/2)<<endl;
return 0;
}
}
return 114514;
}
}//namespace solver_or
int main() {
cin>>n>>q;
for(int i=1;i<=n;++i)cin>>a[i];
if(q==1)return solver_and::main();
if(q==2)return solver_xor::main();
if(q==3)return solver_or::main();
return 0;
}
相关题目推荐:
CF1285D Dr. Evil Underscores 和本题\(\operatorname{AND}\)运算中用到的方法类似:从高到低位考虑,维护一个可选集合。
day7-字符串
子序列匹配问题(给定一个字符串\(s\),问它是不是另一个字符串\(t\)的子序列),有一个经典的贪心方法。逐个考虑\(s\)的每一位,设当前考虑了\(s_{1\dots i}\),在\(t\)上匹配到位置\(j\)(即\(s_{1\dots i}\)是\(t_{1\dots j}\)的子序列,且\(j\)是满足这样条件的最小的\(j\))。接下来直接让\(j\)跳到\(t\)上\(j\)之后的、第一个等于\(s_{i+1}\)的位置即可。如果找不到这样的位置,则说明匹配失败:\(s\)不是\(t\)的子序列。
对于本题,可以把这个贪心的过程搬到DP上。
设\(dp[i][j]\),表示我们构造出的串,在\(S\), \(T\)上用上述方法贪心地匹配,分别匹配到了第\(i\)、第\(j\)个位置,所需要构造的串的最小长度。预处理出\(S\), \(T\)上每个位置之后第一个\(0\) / \(1\)在哪里出现,则可以\(O(1)\)转移。
这个DP是比较容易的。然而难点在于,如何使字典序最小呢?字典序最小,肯定是要从前往后贪心。但是这个贪心的前提又是使长度最小。我们改变一下\(dp\)数组的定义,变成:此时最少还需要构造多长的串,才能使其是\(S_{i+1\dots n}\)和\(T_{j+1\dots m}\)的公共非子序列。那么在转移时,如果下一位填\(0\)转移到的长度\(\leq\)填\(1\)转移到的长度,我们就让下一位填\(0\),否则让下一位填\(1\)。并且用一个数组记录下转移的路径。这种从后往前的DP,可以用记忆化搜索实现,比较方便。
时间复杂度\(O(nm)\)。
参考代码(片段):
const int MAXN=4000,INF=0x3f3f3f3f;
char s[MAXN+5],t[MAXN+5];
int n,m,dp[MAXN+5][MAXN+5],ns[MAXN+5][2],nt[MAXN+5][2],ps[2],pt[2];
pair<int,pii>nxt[MAXN+5][MAXN+5];
int dfs(int i,int j){
assert(i==n+1||j==m+1||s[i]==t[j]);
if(dp[i][j]!=INF)return dp[i][j];
if(i==n+1&&j==m+1)return dp[i][j]=0;
dp[i][j]=dfs(ns[i][0],nt[j][0])+1;
nxt[i][j]=mk(0,mk(ns[i][0],nt[j][0]));
if(dfs(ns[i][1],nt[j][1])+1<dp[i][j]){
dp[i][j]=dfs(ns[i][1],nt[j][1])+1;
nxt[i][j]=mk(1,mk(ns[i][1],nt[j][1]));
}
return dp[i][j];
}
void get_res(int i,int j,string& res){
if(i==n+1&&j==m+1)return;
res+=(char)(nxt[i][j].fi+'0');
get_res(nxt[i][j].se.fi,nxt[i][j].se.se,res);
}
int main() {
cin>>n>>m>>(s+1)>>(t+1);
ps[0]=ps[1]=n+1;
pt[0]=pt[1]=m+1;
ns[n+1][0]=ns[n+1][1]=n+1;
nt[m+1][0]=nt[m+1][1]=m+1;
for(int i=n;i>=1;--i)ns[i][0]=ps[0],ns[i][1]=ps[1],ps[s[i]-'0']=i;
for(int i=m;i>=1;--i)nt[i][0]=pt[0],nt[i][1]=pt[1],pt[t[i]-'0']=i;
memset(dp,0x3f,sizeof(dp));
int ans0=dfs(ps[0],pt[0])+1;
//cout<<ans0<<endl;
string res0="0";
get_res(ps[0],pt[0],res0);
//cout<<res0<<endl;
memset(dp,0x3f,sizeof(dp));
memset(nxt,0,sizeof(nxt));
int ans1=dfs(ps[1],pt[1])+1;
//cout<<ans1<<endl;
string res1="1";
get_res(ps[1],pt[1],res1);
//cout<<res1<<endl;
if(ans0<=ans1)cout<<res0<<endl;
else cout<<res1<<endl;
return 0;
}
相关题目推荐:
day7-序列
考虑最终每个数的出现次数,一定是\(2^x-1\)的形式(即二进制下全是\(1\))。也就是说,对于每个数值,假设当前已经选了\(2^x-1\)个,那么下一次如果要选该数值,必定一次新增\(2^x\)个。当然,我们不一定盯着一个值选。可能由于该数值已经选了过多(\(x\)太大),导致选该数值不如选一个比它更大、但出现次数更少的数划算。更直观地讲,我们可以把每次的选择,列成一张表格,行表示值,列表示该值新增的出现次数:
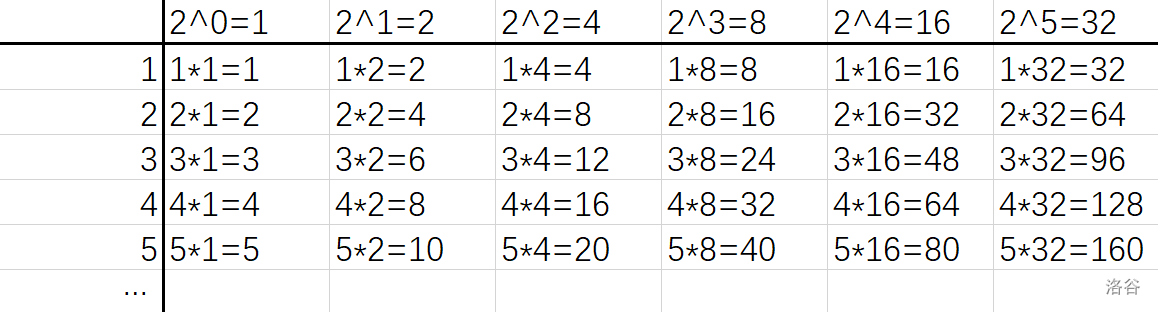
我们要做的,就是在该表格中,选择尽量多的格子,使其权值和\(\leq n\)。
根据贪心,我们肯定先选权值小的格子。所以可以二分我们选的最大权值,记为\(\text{mx}\)。问题转化为求所有权值权值\(\text{mx}\)的格子的权值和,然后判断是否\(\leq n\)。
这个表格很特殊,它行很多,高达\(O(n)\)级别,列却只有\(O(\log n)\)级别。所以我们枚举每一列,可以\(O(1)\)算出要从这一列里选多少个。知道选多少个后,求这一列的和,就相当于\(2^x\)乘以一个等差数列,也可以\(O(1)\)计算。
需要注意的是,等于\(\text{mx}\)的数,可能一部分选,一部分不选,要注意判断。
二分出最大权值后,我们再重复一遍二分的过程,就能求出选到的数量了。
单次询问时间复杂度\(O(\log^2n)\)。
参考代码(片段):
ull n,sn,sum,cnt;
bool check(ull mx){
sum=0;cnt=0;
--mx;
for(int i=0;i<=60;++i){
ull lim=mx/(1ull<<i);
if(lim>sn||(lim+1)*lim/2>n/(1ull<<i))return false;
sum+=(lim+1)*lim/2*(1ull<<i);
cnt+=lim;
if(sum>n)return false;
}
++mx;
ull rest=n-sum;
for(int i=0;i<=60;++i){
if(mx%(1ull<<i)==0){
if(rest<mx)break;
rest-=mx;
cnt++;
}
else break;
}
if(rest==n-sum)return false;
sum=n-rest;
return true;
}
int main() {
int T;cin>>T;while(T--){
cin>>n;
sn=sqrt(n);sn<<=1;
ull l=1,r=n;
while(l<r){
ull mid=(l+r+1)>>1;
if(check(mid))l=mid;
else r=mid-1;
}
check(l);
//cout<<sum<<endl;
cout<<cnt<<endl;
}
return 0;
}
day7-交换
先假设所有数字互不相同。我们从小到大考虑每个数字。那么根据题目要求,当前数字,要么放在开头,要么放在结尾。
对于一次交换操作,我们在较小的数上计算其代价。于是,把当前数挪到前面的代价,就是其前面还未考虑过的数的数量。同理,挪到后面的代价,就是其后面还未考虑过的数的数量。容易发现,当前数无论放在前面还是放在后面,都不影响它后面数的代价,因为代价只和未考虑的数有关。所以可以贪心地:哪种移动方式代价小,就移到哪里。至于求代价,用支持带点修改、区间求和的数据结构(如线段树)简单维护即可。
当有重复的数字时,最优情况下,相同数字间是不会发生交换的:即,所有交换完成后,相同数字间的相对顺序不变。因为如果发生了交换,那么不做这次交换一定能使答案更优。但是用上述的方法,可能就会计算相同数字间的交换。为了避免这种情况,我们按每个值考虑:先把当前值的所有出现位置,都设置为“已考虑”。这样就能避免交换两个相同值的问题了。
时间复杂度\(O(n\log n)\)。
参考代码(片段):
const int MAXN=3e5;
struct SegmentTree{
int sum[MAXN*4+5];
void build(int p,int l,int r){
if(l==r){sum[p]=1;return;}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
sum[p]=sum[p<<1]+sum[p<<1|1];
}
void modify(int p,int l,int r,int pos,int x){
if(l==r){sum[p]+=x;return;}
int mid=(l+r)>>1;
if(pos<=mid)modify(p<<1,l,mid,pos,x);
else modify(p<<1|1,mid+1,r,pos,x);
sum[p]=sum[p<<1]+sum[p<<1|1];
}
int query(int p,int l,int r,int ql,int qr){
if(ql>qr)return 0;
if(ql<=l && qr>=r)return sum[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid)res+=query(p<<1,l,mid,ql,qr);
if(qr>mid)res+=query(p<<1|1,mid+1,r,ql,qr);
return res;
}
SegmentTree(){}
}T;
int n,a[MAXN+5];
pii p[MAXN+5];
int main() {
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i],p[i]=mk(a[i],i);
sort(p+1,p+n+1);
T.build(1,1,n);
ll ans=0;
for(int i=1;i<=n;++i){
int j=i;
while(j+1<=n&&p[j+1].fi==p[i].fi)++j;
for(int k=i;k<=j;++k){
T.modify(1,1,n,p[k].se,-1);
}
for(int k=i;k<=j;++k){
int vl=T.query(1,1,n,1,p[k].se-1);
int vr=T.query(1,1,n,p[k].se+1,n);
ans+=min(vl,vr);
}
i=j;
}
cout<<ans<<endl;
return 0;
}
day9-排列
先不考虑字典序,我们先求出\(\sum_{j=1}^{n}[a_i<b_{i_j}]\)的最大值。我们把找到一对\(a_i\),\(b_j\)使得\(a_i<b_j\),称为发生了一次“匹配”。容易发现,要求的就是最大的匹配数量。有一种简单的贪心方法。将\(a\), \(b\)序列分别排序。从小到大依次考虑每个\(a_i\),让它和当前未使用过的、第一个比它大的\(b_j\)匹配,然后将这个\(b_j\)标记为已使用,继续考虑下一个\(a_{i+1}\),直到找不到这样的\(j\)为止。此时求出的,就是最大匹配数。记为\(\text{num}\)。
那么如何安排,使得\(\sum_{j=1}^{n}[a_i<b_{i_j}]=\text{num}\)的前提下,让\(b\)序列的字典序最大呢?
这类最优化字典序的问题,一般采用的方法是逐位确定答案。也就是说,依次枚举每一位\(i\),再从大到小枚举\(b_i\)填什么。然后判断,如果\(b_i\)填了当前值后,\(b_{i+1\dots n}\)是否至少还存在一种填法,使答案能达到\(\text{num}\)。如果判断为“是”,则\(b_i\)就填当前值了;否则,说明\(b_i\)还需要变得更小。
如果按照一开始所说的这种贪心方法来做判断,那么每次判断的时间复杂度是\(O(n)\)的。又因为还要枚举\(i\)和\(b_i\)的值,所以总时间复杂度\(O(n^3)\)。无法通过本题。
发现,当\(b_i\)从大到小变化时,每次重新判断,似乎有点太暴力了。既然枚举\(i\)和\(b_i\)的值不好避免,那么就尝试优化这个判断的过程。
考虑一开始的贪心。我们从小到大,依次让每个\(a_i\)匹配第一个能匹配的\(b_j\)。还有一种和它等价的贪心:从大到小,依次让每个\(b_j\),去匹配最后一个(也就是最大的、最靠右的)能匹配的\(a_k\)。称这两个贪心分别为“第一种贪心”、“第二种贪心”。
我们枚举的\(b_i\)的值是从大到小变化的。最开始,也就是\(b_i\)最大时,我们先对\(b_{i+1\dots n}\)用第一种贪心,求一遍答案。然后随着\(b_i\)逐渐变小,我们用比\(b_i\)大的这段\(b\),去做第二种贪心。假设,比\(b_i\)大的所有\(b\),它们做第二种贪心,匹配到的最后一个位置为\(a_k\)。那么,\(a_{1\dots k-1}\)仍然是用第一种贪心,这个贪心的数量,对于每个前缀\(k\),我们可以预处理出来。于是,从大到小枚举\(b_i\)取值的过程,就是整个序列,在从第一种贪心,逐步转为第二种贪心的过程。当前,这两个贪心拼合在一起,也就是任意一个中间状态,显然还是最优的,也就是和单独做某一种贪心是等价的。于是,我们就一边枚举\(b_i\)的值,一边顺便维护出了后面的最大答案,也就是完成了原本单独做一次需要\(O(n)\)的这个“判断”。
现在,总时间复杂度\(O(n^2)\)。
参考代码(片段):
const int MAXN=5000;
int n,b[MAXN+5],res[MAXN+5];
pii a[MAXN+5];
bool used_b[MAXN+5];
int main() {
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i].fi,a[i].se=i;
for(int i=1;i<=n;++i)cin>>b[i];
sort(a+1,a+n+1);sort(b+1,b+n+1);
int max_num=0;
for(int i=1,j=0;i<=n;++i){
while(j+1<=n && a[j+1].fi<b[i])++j;
if(j>max_num)++max_num;
}
//cout<<"maxnum "<<max_num<<endl;
int cur_num=0;
for(int i=1;i<=n;++i){
//逐位确定b序列
static int aa[MAXN+5];
static pii bb[MAXN+5],pre[MAXN+5];
int cnt_a=0,ai=0,cnt_b=0;
for(int j=1;j<=n;++j){
if(a[j].se>i)aa[++cnt_a]=a[j].fi;
if(a[j].se==i)ai=a[j].fi;
if(!used_b[j])bb[++cnt_b]=mk(b[j],j);
}
int tmp_num=0;
for(int j=1,k=0;j<cnt_b;++j){
while(k+1<=cnt_a && aa[k+1]<bb[j].fi)++k;
if(k>tmp_num){
++tmp_num;
pre[tmp_num]=mk(tmp_num,j);
}
}
for(int j=tmp_num+1;j<=cnt_a;++j)
pre[j]=pre[j-1];
if(cur_num+tmp_num+(ai<bb[cnt_b].fi)==max_num){
res[i]=bb[cnt_b].fi;
used_b[bb[cnt_b].se]=1;
cur_num+=(ai<bb[cnt_b].fi);
continue;
}
tmp_num=0;
for(int j=cnt_b-1,k=cnt_a,l=cnt_a;j>=1;--j){
while(k>=1 && aa[k]>=bb[j+1].fi)--k;
if(k>=1)--k,++tmp_num;
l=min(l,k);
while(l>=1 && pre[l].se>=j)--l;
if(cur_num+pre[l].fi+tmp_num+(ai<bb[j].fi)==max_num){
res[i]=bb[j].fi;
used_b[bb[j].se]=1;
cur_num+=(ai<bb[j].fi);
break;
}
}
assert(res[i]!=0);
}
for(int i=1;i<=n;++i)
cout<<res[i]<<" \n"[i==n];
return 0;
}
day9-分组
先把所有学生,按\(s_i\)从小到大排序(下文所说的\(s\),都是排好序后的序列)。那么,每一组的极差,就相当于是本组最后一个学生的\(s\)值减去本组第一个学生的\(s\)值。我们把每组的第一个和最后一个学生称为本组的“开头”和“结尾”。依次考虑每个学生,则当前的小组,可以分为“已经结尾的”和“还未结尾的”。也就是说,对于“已经结尾的”小组,它的“结尾”,肯定是已经考虑过的某个学生;而另一种小组的“结尾”,则是之后的某个学生。
于是可以做一个DP。设\(dp[i][j][S]\),表示考虑了前\(i\)个学生,当前还未结尾的小组有\(j\)个,此时的极差之和为\(S\)的方案数。这里的“极差之和”\(S\),其实具体来讲,应该说是前\(i\)个学生,对极差的贡献之和。每个学生对极差的贡献,前面已经提到:如果他是一组的开头,则贡献为\(-s_i\);如果是一组的结尾,则贡献为\(s_i\);否则贡献为\(0\)。据此可以写出三种转移:
- 如果当前学生是某一组的开头。那么我们让\(j\)增大\(1\),\(S\)减小\(s_i\)。
- 如果当前学生是某一组的结尾。那么我们让\(j\)减小\(1\),\(S\)增大\(s_i\)。转移时,要乘以系数,也就是在前面任选一组加入的方案数,为\(j\)。
- 如果当前学生,既不是开头,也不是结尾(或者他所在的学习小组里只有他一个人),则\(j\)和\(S\)都不变。转移时要乘以系数\(j+1\),因为既可能新加入前面\(j\)组中的一组,也可能自己作为一个“单人组”。
最终答案就是:\(dp[n][0][0\dots k]\)之和。
直接DP的时间复杂度为\(O(n^2\sum s)\)。无法通过本题。
考虑优化。可以发现因为最终我们只需要询问\(S=0\dots k\)的位置,那么一个自然的想法是如果\(S\)超出\(k\)我们直接把这个状态丢弃掉。但是因为我们在转移的过程中,\(S\)同样可能会变小,所以直接做并不可行。
我们要想个办法,让\(S\)在转移时只有加、没有减。也就是说,每个位置对极差的“贡献”都要是一个非负数。考虑做差分!设\(d_i=s_i-s_{i-1}\) (\(i>1\))。那么对于一个学习小组,设开头为\(i\),结尾为\(j\),它的极差就是:\(\sum_{t=i+1}^{j}d_t\)。也就是说,我们把贡献摊到了每个\(d\),并且\(d\)数组显然是非负的,于是就可以舍弃掉第三维大于\(k\)的状态了!状态数精简为\(O(n^2k)\)。
转移时,新的第三维\(S'\)就等于\(S+d_i\cdot j\)。
时间复杂度\(O(n^2k)\)。
参考代码(片段):
const int MOD=1e9+7;
inline int mod1(int x){return x<MOD?x:x-MOD;}
inline int mod2(int x){return x<0?x+MOD:x;}
inline void add(int& x,int y){x=mod1(x+y);}
inline void sub(int& x,int y){x=mod2(x-y);}
inline int pow_mod(int x,int i){int y=1;while(i){if(i&1)y=(ll)y*x%MOD;x=(ll)x*x%MOD;i>>=1;}return y;}
const int MAXN=500,MAXK=1000;
int n,k,a[MAXN+5],dp[2][MAXN+5][MAXK+5];
int main() {
cin>>n>>k;
for(int i=1;i<=n;++i)cin>>a[i];
sort(a+1,a+n+1);
dp[0][0][0]=1;
for(int i=1,cur=1;i<=n;++i,cur^=1){
int pre=cur^1;
memset(dp[cur],0,sizeof(dp[cur]));
for(int j=0;j<i;++j){
for(int S=0;S<=k;++S)if(dp[pre][j][S]){
int newS=S+j*(a[i]-a[i-1]);
if(newS>k)break;
//开头
add(dp[cur][j+1][newS],dp[pre][j][S]);
//结尾
if(j)add(dp[cur][j-1][newS],(ll)dp[pre][j][S]*j%MOD);
//既非开头 也非结尾
add(dp[cur][j][newS],(ll)dp[pre][j][S]*(j+1)%MOD);
}
}
}
int cur=n&1,ans=0;
for(int S=0;S<=k;++S)add(ans,dp[cur][0][S]);
cout<<ans<<endl;
return 0;
}
day9-异或
引理:
我们定义一个点的“点权”为它所有出边(含它与父亲之间的边)的边权异或和。那么,“所有边权都为\(0\)”,就等价于“所有点权都为\(0\)”,它们互为充分必要条件。
证明:“所有点权为\(0\)”是“所有边权为\(0\)”的充分必要条件。
【必要性】比较显然。根据点权的定义,边权均为\(0\)时,所有点点权一定为\(0\)。
【充分性】对\(n\)归纳。\(n=1\)时显然成立。\(n>1\)时,若对\(n-1\)成立,我们考虑添加一个叶子。因为点权为\(0\),且叶子只有一条出边,所以叶子的边权也为\(0\)。所以整棵树边权都为\(0\)。
考虑一次操作对点权的影响,发现相当于选择两个点\(u\), \(v\),然后让\(u\), \(v\)的点权同时异或上一个数\(x\)。
于是问题转化为,有\(n\)个数\(a_1,a_2,\dots a_n\),每次可以选择两个数\(a_u\), \(a_v\),把它们异或上同一个值。目标是让所有数字均为\(0\),求最小操作次数。
先考虑怎么让它们全变成\(0\)。暴力的做法是从左到右,依次把每个数消成\(0\)。那最后一个数怎么办呢?其实,最后一个数不用做任何操作,轮到它时,它一定是\(0\)。这是因为,树上每条边在恰好两个点的点权里出现,所以\(a_1\dots a_n\)的异或和一定为\(0\)。
所以,最多只需要做\(n-1\)次操作,就能把所有数都变为\(0\)。但这样不一定是最优的。经过上面的分析,可以发现,对于任意\(k\)个异或和为\(0\)的数,只需要\(k-1\)次操作,就能将它们全部变为\(0\)。因此,我们要把\(a\)序列分为尽可能多的、异或和为\(0\)的组,因为每分出一组,就能使答案减少\(1\)。
由于边权的范围是\([0,15]\),所以点权一定也在这个范围内。首先,等于\(0\)的数不用管,因为它既不需要我们操作,也不会对其他数的操作产生贡献。其他数字,如果出现次数大于等于\(2\)次,那么一定每两个放到一组(反证法,如果两个相同的数,被分到两个不同的组,则可以把这两个相同的数放到一起,原来它们各自所在的组放到一起)。
所以,每种值,最后只会剩\(1\)个或\(0\)个(取决于他们原本的数量是奇数还是偶数)。我们只需要对这不超过\(15\)个数分组。可以做状压DP。设\(dp[s]\)表示已经考虑了\(s\)里的数,最多能分出多少组。预处理出每个集合是否异或和为\(0\)。转移时,枚举\(s\)的一个异或和为\(0\)的子集\(t\),用\(dp[s\setminus t]\)更新\(dp[s]\)。
时间复杂度\(O(n+3^w)\),其中\(w\)为权值,\(w\leq 15\)。
参考代码(片段):
const int MAXN=1e5;
int n,m,a[MAXN+5],c[16],v[17],s[1<<16],dp[1<<16],ans;
int main() {
cin>>n;
for(int i=1,u,v,w;i<n;++i){
cin>>u>>v>>w;
a[u]^=w,a[v]^=w;
}
for(int i=1;i<=n;++i)c[a[i]]++;
for(int i=1;i<16;++i){
ans+=(c[i]>>1);
if(c[i]&1)v[++m]=i;
}
for(int i=0;i<(1<<m);++i){
for(int j=1;j<=m;++j){
if(i&(1<<(j-1)))s[i]^=v[j];
}
}
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<(1<<m);++i){
if(s[i]==0)dp[i]=__builtin_popcount(i)-1;
for(int j=i;j;j=i&(j-1)){
assert((i&j)==j && (i|j)==i);//j是i的一个子集
if(s[j]==0)dp[i]=min(dp[i],dp[i^j]+__builtin_popcount(j)-1);
}
}
cout<<ans+dp[(1<<m)-1]<<endl;
return 0;
}
day10-旅行
考虑二分答案\(\text{mid}\)。那么,此时距离\(\geq 2\cdot \text{mid}\)的点之间就可以通过,否则就不能通过。我们反过来考虑:在所有距离\(<2\cdot \text{mid}\)的点之间连边,把上、下边界也看做两个“点”,那么,如果上、下边界之间连通,就说明有一段路被堵死了,当前\(\text{mid}\)无解。否则\(\text{mid}\)就是可以的。
但是二分答案复杂度太高。我们考虑这个过程等价于什么。
对于这张\(k+2\)个点的图,我们定义两点间的边权是它们欧几里得距离的一半。那么二分\(\text{mid}\)后,相当于只考虑所有边权\(<2\cdot \text{mid}\)的边,问有没有从上边界点(\(k+1\))到下边界点(\(k+2\))的路径。
在原图上,我们定义一条路径的长度,是路径上所有边边权的最大值。那么,\(\text{mid}\)无解,当且仅当存在一条从\(k+1\)到\(k+2\)的路径长度\(\leq \text{mid}\)(这样就被堵死了)。所以我们不用二分\(\text{mid}\),而是直接求从\(k+1\)到\(k+2\)的最短路长度即可!
因为这个图非常特殊,点数很少而边数很多,所以可以直接用不加堆优化的dijkstra算法,时间复杂度\(O(k^2)\)。
参考代码(片段):
const int MAXK=7000;
int n,m,K;
double dis[MAXK+5];
bool vis[MAXK+5];
struct Point_t{
int x,y;
}p[MAXK+5];
double get_dist(double x1,double y1,double x2,double y2){
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main() {
cin>>n>>m>>K;
for(int i=1;i<=K;++i){
cin>>p[i].x>>p[i].y;
dis[i]=m-p[i].y;
}
dis[0]=m;
while(true){
int u=0;
for(int i=1;i<=K;++i)if(!vis[i] && dis[i]<dis[u])u=i;
if(!u){
cout<<setiosflags(ios::fixed)<<setprecision(10)<<dis[u]/2<<endl;
return 0;
}
vis[u]=1;
dis[0]=min(dis[0],max(dis[u],(double)p[u].y));
for(int i=1;i<=K;++i)if(!vis[i]){
dis[i]=min(dis[i],max(dis[u],get_dist(p[i].x,p[i].y,p[u].x,p[u].y)));
}
}
return 114514;
}
day10-寻宝
乱搞做法:
二分答案。
check时,每一轮,先把所有点把所有点random_shuffle一下。然后依次考虑每个点,如果从当前边界能走到该点,就直接走过去,然后立即更新边界,继续考虑后面的点。如果所有点都访问过,直接反回\(\texttt{true}\)。如果这一轮没走到任何点(边界没有被更新过),反回\(\texttt{false}\)。否则进行下一轮。
最坏时间复杂度是\(O(n^2\log x)\)。但可以AC。
参考代码(片段):
bool check(long long mid){
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;++i){
if(p[i].x<=1 && p[i].y<=1){
vis[p[i].id]=1;
}
}
int curx=1,cury=1;
while(true){
random_shuffle(p+1,p+n+1);
bool allvis=true;
bool newpoint=false;
for(int i=1;i<=n;++i){
if(vis[p[i].id])continue;
allvis=false;
if(2LL*(max(0,p[i].x-curx)+max(0,p[i].y-cury))<=mid){
vis[p[i].id]=1;
newpoint=true;
curx=max(curx,p[i].x);
cury=max(cury,p[i].y);
}
}
if(allvis)return true;
if(!newpoint)return false;
}
}
正解:
在任意的时刻,我们可以把“宝藏”分为四类:(1) 位于已经探索过的区域里的宝藏,(2) 位于区域右上角,(3) 位于区域正上方,(4) 位于区域正右方。
第(1)种可以直接加入,不需要新花费木棒。对于后面三种,我们想到一个贪心策略:算出加入每个点,需要新花费的木棒数,然后选花费最小的加入,并更新区域边界。考虑为什么这样贪心是对的。因为随着加点过程的进行,边界只会扩大不会缩小,所以加入每个点的代价只会不断减小。我们要最小化“新增数量的最大值”,所以显然每次选最小的加入是最优的。
那么问题转化为,如何快速选出花费最小的点。
考虑(2),(3),(4)三类点的花费分别是什么。假设当前已探索区域右上角为\((x_0,y_0)\),新加入的点坐标为\((x_1,y_1)\)。那么,新加入第(2)类点的花费为\(2(x_1-x_0+y_1-y_0)\)。新加入第(3)类点的花费为\(2(y_1-y_0)\)。新加入第(4)类点的花费为\(2(x_1-x_0)\)。
对于第(3)类点,我们相当于对于一个横坐标的前缀,求里面\(y\)坐标最小的点。同理,对于第(4)类点,我们相当于对一个纵坐标的前缀,求里面\(x\)坐标最小的点。当然,这里面可能混杂着一些第(1)类的点,我们要支持把它们“删除”,下面会讲具体怎么做。
可以用两个小根堆维护。以第(3)类点的堆为例,这个堆里点按\(y\)坐标为关键字,每次弹出\(y\)坐标最小的。当已探索区域的\(x\)坐标扩大时,就把新加入的这些\(x\)坐标上的点放入这个堆里。当需要弹出堆顶元素时,用一个while循环,直到弹出的不是第(1)类为止(相当于用这种方法实现“把第(1)类点删除”的效果)。
对于第(2)类,可以不需要堆。一开始直接把所有点按\(x+y\)排序。用一个指针,初始时指向\(1\)。如果当前元素是第(1),(3),(4)类,就把指针\(\texttt{++}\)。直到找到第(2)类元素为止。仔细想想,第(2)类点不需要堆,是因为它们没有“横/纵坐标上一个前缀”这个限制,所以没有“加入”操作。直接用这个预先排好序的数组,指针指向的点,就相当于“堆顶”了。
每次,取(2),(3),(4)类的堆顶,比一比谁花费最小,就把谁加入。
时间复杂度\(O(n\log n)\)。
参考代码(片段):
const int MAXN=3e5;
const ll INF=4e9;
int n,x[MAXN+5],y[MAXN+5];
int sorted_x[MAXN+5],sorted_y[MAXN+5],sorted_xy[MAXN+5];
bool vis[MAXN+5];
bool cmp_x(int i,int j){return x[i]<x[j];}
bool cmp_y(int i,int j){return y[i]<y[j];}
bool cmp_xy(int i,int j){return x[i]+y[i]<x[j]+y[j];}
int main() {
cin >> n;
for ( int i = 1 ; i <= n ; ++ i) {
cin >> x[i] >> y[i] ;
sorted_x[i] = sorted_y[i] = sorted_xy[i] = i ;
}
sort ( sorted_x + 1 , sorted_x + n + 1 , cmp_x ) ;
sort ( sorted_y + 1 , sorted_y + n + 1 , cmp_y ) ;
sort ( sorted_xy + 1 , sorted_xy + n + 1 , cmp_xy ) ;
priority_queue<pii>q_x,q_y;
int cur_x=1,cur_y=1;
int idx_x=0,idx_y=0,idx_xy=0;
for(int t=1;t<=n;++t){
while(idx_x+1<=n && x[sorted_x[idx_x+1]]<=cur_x){
++idx_x;
q_y.push(mk(-y[sorted_x[idx_x]],sorted_x[idx_x]));
}
while(idx_y+1<=n && y[sorted_y[idx_y+1]]<=cur_y){
++idx_y;
q_x.push(mk(-x[sorted_y[idx_y]],sorted_y[idx_y]));
}
while(idx_xy+1<=n && (vis[sorted_xy[idx_xy+1]] || x[sorted_xy[idx_xy+1]]<=cur_x || y[sorted_xy[idx_xy+1]]<=cur_y))
++idx_xy;
while(!q_x.empty() && vis[q_x.top().se])q_x.pop();
while(!q_y.empty() && vis[q_y.top().se])q_y.pop();
if(!q_x.empty() && -q_x.top().fi<=cur_x){
int res=q_x.top().se;
cout<<res<<" ";
vis[res]=1;
cur_x=max(cur_x,x[res]);
cur_y=max(cur_y,y[res]);
continue;
}
if(!q_y.empty() && -q_y.top().fi<=cur_y){
int res=q_y.top().se;
cout<<res<<" ";
vis[res]=1;
cur_x=max(cur_x,x[res]);
cur_y=max(cur_y,y[res]);
continue;
}
pair<ll,int>res=mk(INF,0);
if(!q_x.empty())
res=min(res,mk(2LL*(-q_x.top().fi-cur_x),q_x.top().se));
if(!q_y.empty())
res=min(res,mk(2LL*(-q_y.top().fi-cur_y),q_y.top().se));
if(idx_xy+1<=n)
res=min(res,mk(2LL*(x[sorted_xy[idx_xy+1]]-cur_x+y[sorted_xy[idx_xy+1]]-cur_y),sorted_xy[idx_xy+1]));
assert(res!=mk(INF,0));
cout<<res.se<<" ";
vis[res.se]=1;
cur_x=max(cur_x,x[res.se]);
cur_y=max(cur_y,y[res.se]);
}
return 0;
}
day10-鞋子
我们先不考虑方向的问题,假设只要是相邻的左右脚就能匹配。那么,问题相当于求二分图最大匹配:左、右脚的格子分别是二分图的两边,两个格子相邻就连边。
然后考虑方向。如果有至少一只鞋子没有匹配,则可以通过它调整它周围所有鞋的方向。同理,也可以先通过它周围的鞋去调整更外面的鞋。所以最后一定能把每个格子调成任何我们想要的方向。
剩下的就是所有格子都匹配的情况。也就是\(nm\)为偶数,且最大匹配数为\(\frac{nm}{2}\)。根据上面的讨论,此时答案要么是\(\frac{nm}{2}\),要么是\(\frac{nm}{2}-1\)(也就是空出一双鞋子用来调整别的鞋的方向)。发现,如果我们把四个方向编号为\(0,1,2,3\),那么一次操作后,两个格子一个\(+1\),一个\(-1\)(\(\bmod4\)意义下),总和\(\bmod4\)不变!于是我们猜想,所有格子如果能自己调整过来(答案等于\(\frac{nm}{2}\)),当且仅当它们总和\(\bmod 4\)与目标状态相等。而知道匹配关系以后,目标状态是很好计算的。
可以证明,这个结论是对的。具体来说,就是证明【所有完美匹配的权值和对\(4\)取模的结果相同】,以及【任意权值和对\(4\)取模后相同的状态是相互可达的】这两个结论。详见官方题解。
时间复杂度\(O(nm\sqrt{nm})\)。
参考代码(片段):
const int MAXN=105,INF=1e9;
const int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
string s1[MAXN],s2[MAXN];
int val[233];
int n,m,X1[MAXN],Y1[MAXN],X2[MAXN],Y2[MAXN];
bool inmap(int i,int j){return i>=1&&i<=n&&j>=1&&j<=m;}
int id(int i,int j){return (i-1)*m+j;}
struct EDGE{int nxt,to,w;}edge[2000005];
int head[10010],tot;
inline void add_edge(int u,int v,int w){
edge[++tot].nxt=head[u];edge[tot].to=v;edge[tot].w=w;head[u]=tot;
edge[++tot].nxt=head[v];edge[tot].to=u;edge[tot].w=0;head[v]=tot;
}
int dep[10010],cur[10010];
bool bfs(int s,int t){
queue<int>q;
q.push(s);
for(int i=1;i<=t;++i)dep[i]=0;
dep[s]=1;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=edge[i].nxt){
int v=edge[i].to;
if(edge[i].w&&!dep[v]){
dep[v]=dep[u]+1;
if(v==t)return 1;
q.push(v);
}
}
}
return 0;
}
int dfs(int u,int flow,int t){
if(u==t)return flow;
int rest=flow;
for(int &i=cur[u];i&&rest;i=edge[i].nxt){
int v=edge[i].to;
if(dep[v]==dep[u]+1&&edge[i].w){
int k=dfs(v,min(rest,edge[i].w),t);
if(!k){dep[v]=0;continue;}
edge[i].w-=k;
edge[i^1].w+=k;
rest-=k;
}
}
return flow-rest;
}
int eid[MAXN][MAXN][4];
int solve(){
tot=1;int s=n*m+1,t=n*m+2;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(s1[i][j]=='L'){
for(int k=0;k<4;++k){
int ii=i+dx[k],jj=j+dy[k];
if(inmap(ii,jj) && s1[ii][jj]=='R'){
add_edge(id(i,j),id(ii,jj),1);
eid[i][j][k]=tot;
}
}
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(s1[i][j]=='L')add_edge(s,id(i,j),1);
else add_edge(id(i,j),t,1);
}
}
int maxflow=0,tmp;
while(bfs(s,t)){
for(int i=1;i<=t;++i)cur[i]=head[i];
while(tmp=dfs(s,INF,t))maxflow+=tmp;
}
return maxflow;
}
int main() {
ios::sync_with_stdio(0);//syn!!!
cin>>n>>m;
for(int i=1;i<=n;++i){cin>>s1[i];s1[i]="@"+s1[i];}
for(int i=1;i<=n;++i){cin>>s2[i];s2[i]="@"+s2[i];}
val['U']=0;val['R']=1;val['D']=2;val['L']=3;
int ans=solve();
if((n*m)%2==0&&ans==n*m/2){
int v1=0,v2=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(s1[i][j]=='L'){
for(int k=0;k<4;++k){
if(eid[i][j][k] && edge[eid[i][j][k]].w){
//cout<<i<<" "<<j<<" "<<k<<endl;
v1+=val[(int)s2[i][j]]+val[(int)s2[i+dx[k]][j+dy[k]]];
v2+=k+k;
break;
}
}
}
}
}
if(v1%4!=v2%4)ans--;
}
cout<<ans<<endl;
return 0;
}

