题解 CF1375F Integer Game（构造，博弈）

题目链接

尝试通过构造，让先手赢。

考虑什么情况下，后手不得不让两个堆数量相等。假设某个局面下，三堆里分别有\(a,b,c\)个石头，不妨设\(a>b>c\)。那么如果上一轮的操作对象是\(a\)（这一轮不能对\(a\)操作），且\(a-b=b-c\)。那么此时，如果先手报：\(a-b\)，后手就不得不让两堆数量相等：他要么把\(b\)变成\(a\)，要么把\(c\)变成\(b\)。

总结一下这个条件，就是让上一次的操作对象，变成当前最大的数，且当前三个数从大到小依次差相等。那么此时，只需要一次操作，先手就赢了。如图：

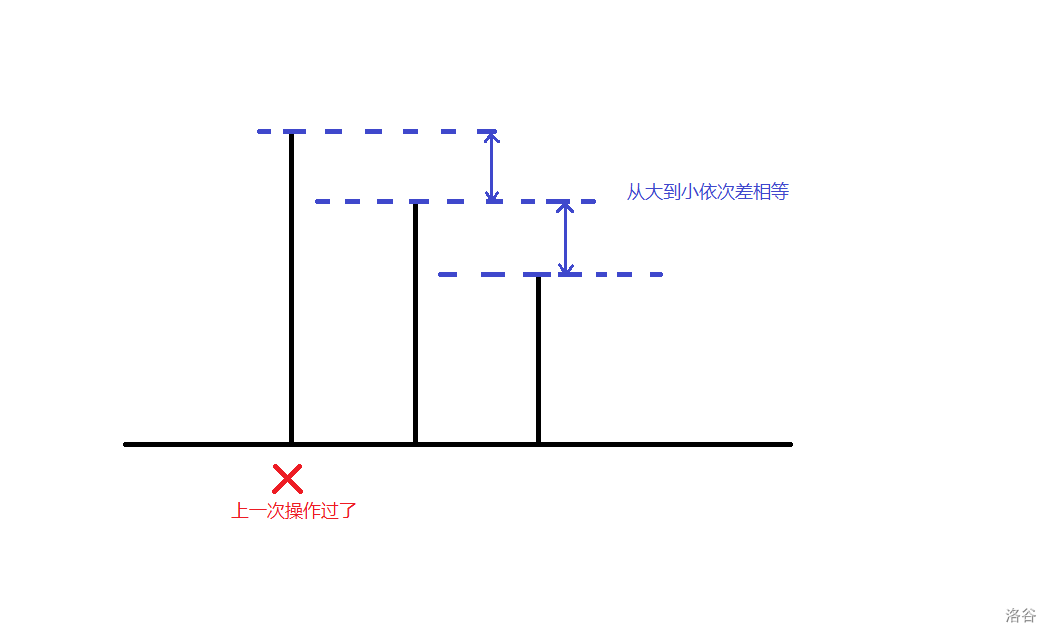
我们进一步思考，如何达到上述的局面呢？还是假设\(a>b>c\)且\(a\)在上一轮被用过。设\(x=a-b\), \(y=a-c\)。此时先手可以报\(x+y\)。那么后手要么让\(b\texttt{+=}x+y\)，要么让\(c\texttt{+=}x+y\)，无论哪种情况，被操作的数都会成为最大值，且三个数从大到小依次差相等！于是就变成了上一种必胜的局面。

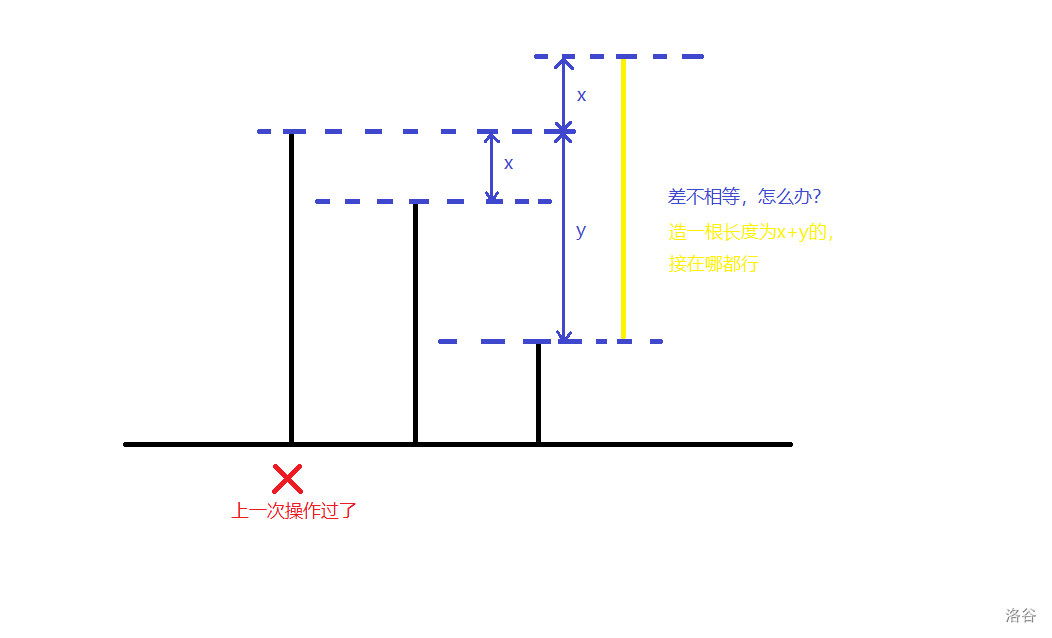
由此可知，只要上一次的操作对象是当前最大的数，先手就一定能用两次操作获胜。

这个条件比第一个条件弱很多，这个局面也很好达到。一开始的时候，不妨还是设\(a>b>c\)，先报\(a-b\)。此时，\(a-b\)要么被作用于\(a\)上（达到效果，使上一次操作对象是当前最大的数），要么被作用于\(c\)上。如果被作用于\(c\)上，下一轮就只能操作\(a\)或\(b\)，我们再报\(a-b\)，后手不能对\(b\)操作（否则\(a=b\)就直接输了），所以后手只能对\(a\)操作，达到了我们希望的局面。

综上所述，我们选先手，在\(4\)步以内，必能获胜。

参考代码：

//problem:F
#include <bits/stdc++.h>
using namespace std;
 
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
 
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
 
ll a[4];
void work(){
	//上一次的操作对象,在操作后是最大值
	for(int i=1;i<=3;++i){
		if(a[i]==max(a[1],max(a[2],a[3]))){
			int j=1,k=2;
			if(i==j)j=3;
			if(i==k)k=3;
			cout<<(a[i]-a[j])+(a[i]-a[k])<<endl;
			int l;
			cin>>l;
			assert(l!=i);
			if(l==0)return;
			if(l==k)swap(j,k);
			//l=j
			a[j]+=(a[i]-a[j])+(a[i]-a[k]);
			cout<<a[i]-a[k]<<endl;
			cin>>l;
			assert(l==0);
			return;
		}
	}
}
int main() {
	cin>>a[1]>>a[2]>>a[3];
	cout<<"First"<<endl;
	for(int i=1;i<=3;++i){
		if(a[i]==max(a[1],max(a[2],a[3]))){
			int j=1;
			if(i==1)j=2;
			cout<<a[i]-a[j]<<endl;
			int k;
			cin>>k;
			a[k]+=a[i]-a[j];
			assert(k!=j);
			if(k==0)return 0;
			else if(k==i)work();
			else{
				if(a[k]>a[i])work();
				else{
					cout<<a[i]-a[j]<<endl;
					int l;
					cin>>l;
					a[l]+=a[i]-a[j];
					assert(l!=k);
					assert(l!=j);
					if(l==0)return 0;
					else work();
				}
			}
			return 0;
		}
	}
	return 0;
}