【2020省选Day1T1】LOJ3299 「联合省选 2020 A | B」冰火战士
这个“比赛方式”被题目描述的花里胡哨,但实际上很简单:
假如设定比赛温度为\(k\)。那么,“有用”的冰系战士,就是\(x_i\leq k\)的这些冰系战士;“有用”的火系战士,就是\(x_i\geq k\)的这些火系战士。一场比赛的价值,就是冰火两方,“有用”的战士的\(y_i\)之和的较小值。具体来说,就是:
\[\min\left(\sum_{i\in\text{ice},x_i\leq k}y_i,\sum_{i\in\text{fire},x_i\geq k}y_i\right) \]我们要选择一个\(k\),使得这个价值尽可能大。如果有多个\(k\)能使价值最大,则选最大的\(k\)。
首先容易发现,最优的\(k\)一定是某名战士的温度。所以我们可以把所有战士的温度先离散化,然后答案就只要在这些值里面找即可。
考虑两个函数,一个是\(f_{\text{ice}}(k)=\sum_{i\in\text{ice},x_i\leq k}y_i\),一个是\(f_{\text{fire}}(k)=\sum_{i\in\text{fire},x_i\geq k}y_i\)。那么,我们就是要取一个\(k\),使得\(\min(f_{\text{ice}}(k),f_{\text{fire}}(k))\)最大。
发现,\(f_{\text{ice}}(k)\)是单调不下降的;\(f_{\text{fire}}(k)\)是单调不上升的。如果把它们一起画出来,大概是“打一个叉”的样子。
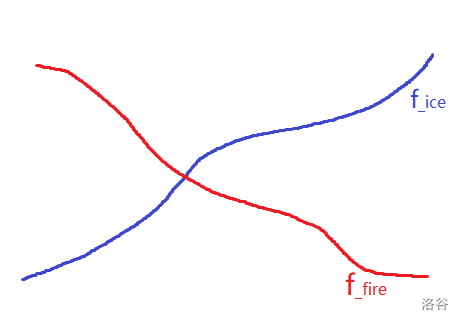
考虑设\(\text{res}(k)=\min(f_{\text{ice}}(k),f_{\text{fire}}(k))\),则画出来应该是这样,也就是图中黑色的这条线。
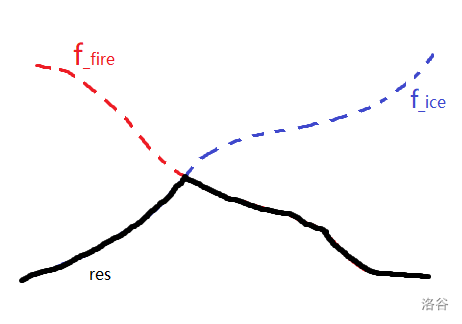
发现,当\(f_{\text{ice}}(k)\)和\(f_{\text{fire}}(k)\)相交时,\(\text{res}(k)\)取到最大值。但是实际上,由于两个函数并不连续(\(k\)只能取整数),所以有两个可能的最优\(k\):
- 一个是,最大的,使得\(f_{\text{ice}}(k)<f_{\text{fire}}(k)\)的\(k\)。
- 另一个是,最小的,使得\(f_{\text{ice}}(k)\geq f_{\text{fire}}(k)\)的\(k\)。
容易想到二分答案。考虑用数据结构维护\(f_{\text{ice}}(k)\)和\(f_{\text{fire}}(k)\),我们需要支持区间加、单点查询。例如,每个冰系战士,是对所有\(k\geq x_i\)(一段后缀),令它们的\(f_{\text{ice}}(k)\)值加上\(y_i\);一个火系战士,是对所有\(k\leq x_i\)(一段前缀),令它们的\(f_{\text{fire}}(k)\)值加上\(y_i\)。(当然,你也可以转化,或者说理解为,单点加,区间求和,这本质上是一样的)。这个数据结构,可以用线段树或树状数组。这样做,时间复杂度是\(O(n\log^2n)\)的,无法AC。
继续优化。你看,又是线段树,又是二分,你很容易想到线段树上二分。对每个区间,维护这个区间左端点的\(f_{\text{ice}}(l)\)和\(f_{\text{fire}}(l)\),右端点的\(f_{\text{ice}}(r)\)和\(f_{\text{fire}}(r)\),就可以二分了。具体来说,我们要做三次“线段树上二分”。第一次,找到【最大的,使得\(f_{\text{ice}}(k)<f_{\text{fire}}(k)\)的\(k\)】。第二次,找到【最小的,使得\(f_{\text{ice}}(k)\geq f_{\text{fire}}(k)\)的\(k\)】(当然,这里第二个\(k\)其实就是第一个\(k\)加\(1\)的位置。但是我们不光要知道位置,还需要知道这个位置上\(\min(f_{\text{ice}}(k),f_{\text{fire}}(k))\)的具体的值,所以还是需要再做一次线段树上操作的)。那么,最大价值,就是这两个\(k\)对应价值的较大者。然而,如果价值较大的\(k\)是第二个,你会发现,它后面,可能还存在价值和它一样的\(k\)。而根据题目要求,如果价值一样,我们要找到最后一个\(k\)。所以此时我们还需要把这个“最大价值”带入,再二分一次,找到价值等于这个“最大价值”的、最靠后的\(k\)。因此,一共需要做三次“线段树上二分”,虽然时间复杂度变成了\(O(n\log n)\),但是常数实在是太大了,最终可能和树状数组实现的\(O(n\log^2n)\)做法得分差不多。
我们继续优化。其实,树状数组上也是可以二分的。这个“二分”的实现,其实更像“倍增”。例如用倍增法求LCA时,我们从大到小枚举当前节点的\(2^{\log n}\dots 2^0\)次祖先,能往上跳就往上跳。在树状数组上也是一样,每次检查从当前点,往前跳\(2^i\)个位置,是否“可行”。如果“可行”,就跳过去。否则位置不变。这里“往前跳\(2^i\)是否可行”怎么“检查”,其实就是看树状数组上\(\text{curpos}+2^i\)的这个位置里填的数。这是由于树状数组的性质:\(c[i]\)里填的是,\([i-\operatorname{lowbit}(i)+1,i]\)这段区间的信息。那么\(\text{curpos}+2^i\),这个位置,填的就是\([\text{curpos}+1,\text{curpos}+2^i]\)这段的信息。
现在我们会在树状数组上二分了。回到本题。我们用树状数组,还是维护\(f_{\text{ice}}(k)\)和\(f_{\text{fire}}(k)\)这两个东西。修改的时候,是区间修改,可以用树状数组的套路:差分,转化为单点修改。具体来说,如果是后缀加,则直接在开始位置加;如果是前缀加,则先用一个全局变量记录,再把后缀减掉(这样只需要一次树状数组上操作)。
查询的时候,先二分出【最大的,使得\(f_{\text{ice}}(k)<f_{\text{fire}}(k)\)的\(k\)】和【最小的,使得\(f_{\text{ice}}(k)\geq f_{\text{fire}}(k)\)的\(k\)】,并查询出它们的\(f\)值。如果第二个\(f\)值更大,则带入这个值,再二分一次。就和线段树的做法类似。所以最多需要3次树状数组上操作。由于树状数组常数小得多,所以可以通过。
时间复杂度\(O(n\log n)\)。
注意:要使用读入优化。
参考代码(在LOJ查看):
//problem:LOJ3299
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
/* --------------- fast io --------------- */ // begin
namespace Fread{
const int SIZE=1<<20;
char buf[SIZE],*S,*T;
inline char getchar(){
if(S==T){
T=(S=buf)+fread(buf,1,SIZE,stdin);
if(S==T)return EOF;
}
return *S++;
}
}//namespace Fread
namespace Fwrite{
const int SIZE=1<<20;
char buf[SIZE],*S=buf,*T=buf+SIZE;
inline void flush(){
fwrite(buf,1,S-buf,stdout);
S=buf;
}
inline void putchar(char c){
*S++=c;
if(S==T)flush();
}
struct _{
~_(){flush();}
}__;
}//namespace Fwrite
#ifdef ONLINE_JUDGE
#define getchar Fread::getchar
#define putchar Fwrite::putchar
#endif
template<typename T>inline void read(T& x){
x=0;int f=1;
char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c))x=x*10+(c-'0'),c=getchar();
x*=f;
}
template<typename T>inline void write(T x,bool _enter=0,bool _space=0){
if (!x)putchar('0');else{
if(x<0)putchar('-'),x=-x;
static char dig[41];
int top=0;
while(x)dig[++top]=(x%10)+'0',x/=10;
while(top)putchar(dig[top--]);
}
if(_enter)putchar('\n');
if(_space)putchar(' ');
}
namespace Fastio{
struct reader{
template<typename T>reader& operator>>(T& x){::read(x);return *this;}
reader& operator>>(char& c){
c=getchar();
while(c=='\n'||c==' ')c=getchar();
return *this;
}
reader& operator>>(char* str){
int len=0;
char c=getchar();
while(c=='\n'||c==' ')c=getchar();
while(c!='\n'&&c!=' ')str[len++]=c,c=getchar();
str[len]='\0';
return *this;
}
}cin;
const char endl='\n';
struct writer{
template<typename T>writer& operator<<(T x){::write(x,0,0);return *this;}
writer& operator<<(char c){putchar(c);return *this;}
writer& operator<<(const char* str){
int cur=0;
while(str[cur])putchar(str[cur++]);
return *this;
}
}cout;
}//namespace Fastio
#define cin Fastio::cin
#define cout Fastio::cout
#define endl Fastio::endl
/* --------------- fast io --------------- */ // end
const int MAXN=2e6;
int m,vals[MAXN+5],cnt_val;
struct Event{
int op,t,x,y;
}ev[MAXN+5];
struct FenwickTree{
int sz;
int fire[MAXN+5],ice[MAXN+5],delta_fire;
void modify_ice(int pos,int val){
//后缀加 -> 单点加,查询时查前缀和
for(int p=pos;p<=sz;p+=(p&(-p))){
ice[p]+=val;
}
}
void modify_fire(int pos,int val){
//前缀加 -> 后缀减,总偏移量加
delta_fire+=val;
for(int p=pos+1;p<=sz;p+=(p&(-p))){
fire[p]-=val;
}
}
int query_min(int pos){//min(ice,fire)
int ice_sum=0,fire_sum=delta_fire;
for(int p=pos;p;p-=(p&(-p))){
ice_sum+=ice[p];
fire_sum+=fire[p];
}
return min(ice_sum,fire_sum);
}
int find1(){
//最后一个ice-fire<0的位置
int p=0,s=-delta_fire;
for(int i=20;i>=0;--i){
if(p+(1<<i)>sz)continue;
int nxt=s+(ice[p+(1<<i)]-fire[p+(1<<i)]);
if(nxt<0){
s=nxt;
p+=(1<<i);
}
}
return p;
}
int find2(int goal_min){
//最后一个min(ice,fire)=val的位置
int p=0,ice_sum=0,fire_sum=delta_fire;
for(int i=20;i>=0;--i){
if(p+(1<<i)>sz)continue;
int new_ice=ice_sum+ice[p+(1<<i)];
int new_fire=fire_sum+fire[p+(1<<i)];
if(new_ice<new_fire){
ice_sum=new_ice;
fire_sum=new_fire;
p+=(1<<i);
}
else{
assert(min(new_ice,new_fire)<=goal_min);
if(min(new_ice,new_fire)==goal_min){
ice_sum=new_ice;
fire_sum=new_fire;
p+=(1<<i);
}
}
}
return p;
}
void resize(int _sz){sz=_sz;}
FenwickTree(){}
}T;
int main() {
//freopen("icefire.in","r",stdin);
//freopen("icefire.out","w",stdout);
cin>>m;
for(int i=1;i<=m;++i){
cin>>ev[i].op;
if(ev[i].op==1){
cin>>ev[i].t>>ev[i].x>>ev[i].y;
vals[++cnt_val]=ev[i].x;
}
else{
int j;cin>>j;
ev[i].t=ev[j].t;
ev[i].x=ev[j].x;
ev[i].y=-ev[j].y;
}
}
sort(vals+1,vals+cnt_val+1);
cnt_val=unique(vals+1,vals+cnt_val+1)-(vals+1);
for(int i=1;i<=m;++i){
ev[i].x=lob(vals+1,vals+cnt_val+1,ev[i].x)-vals;
//cout<<ev[i].x<<endl;
}
T.resize(cnt_val);
for(int i=1;i<=m;++i){
if(ev[i].t==0)
T.modify_ice(ev[i].x,ev[i].y);
else
T.modify_fire(ev[i].x,ev[i].y);
/*
//暴力
pii res=mk(-1,-1);
for(int j=1;j<=cnt_val;++j){
res=max(res,mk(T.query_min(j),j));
}
*/
int p1=T.find1();
pii res1=mk(-1,-1);
if(p1>0){
res1=mk(T.query_min(p1),p1);
}
pii res2=mk(-1,-1);
if(p1<cnt_val){
int goal_min=T.query_min(p1+1);
int p2=T.find2(goal_min);
//assert(p2>=p1+1);
//assert(T.query_min(p2)==goal_min);
//assert(p2==cnt_val||T.query_min(p2+1)<goal_min);
res2=mk(goal_min,p2);
}
pii res=max(res1,res2);
if(res.fi==0)
cout<<"Peace"<<endl;
else
cout<<vals[res.se]<<" "<<res.fi*2<<endl;
}
return 0;
}

