题解 CF506C Mr. Kitayuta vs. Bamboos
因为是“最小化最大值”,容易想到二分答案。设二分值为\(\text{mid}\),我们要判断是否能使最终所有竹子的高度都\(\leq\text{mid}\)。如果从前往后安排每一天,会发现很难找到一种固定的贪心策略,来确定当天砍哪些竹子。
换个角度。考虑最后一天,所有竹子会长高\(a_i\)米。那么在最后一天开始生长之前,第\(i\)个竹子不能高于\(\text{mid}-a_i\)米。
- 如果我们在最后一天不砍第\(i\)个竹子,那么在倒数第二天开始之前,第\(i\)个竹子不能高于\(\text{mid}-2a_i\)米。
- 如果在最后一天砍了第\(i\)个竹子,设砍了\(x\)次,那么在倒数第二天开始之前,第\(i\)个竹子不能高于\(\text{mid}+p\cdot x-2a_i\)米。
以此类推。按照这种“时光倒流”的想法:每个竹子初始高度为\(\text{mid}\),每天高度会减少\(a_i\),我们每用一次砍伐机会可以使其高度增加\(p\)。这里的“高度”,代表的实际含义是:如果之后按照我们确定的这种方式砍伐(因为我们在时光倒流,所以之后的砍伐方式都已经确定了),那么(在正向时间中)当前时刻这根竹子的高度应不高于多少,才能使得最终高度不超过\(\text{mid}\)。根据这个含义,我们要做的就是保证在整个时光倒流的过程中,每根竹子的“高度”始终不能为负。因为一但“高度”为负,意味着要求(正向时间中)高度不得高于一个负数,这显然是不可能的。
关于“时光倒流”,可以结合下面这张图理解。其中蓝色是正向的时间,也就是实际上的高度。绿色是我们时光倒流,确定出的“高度”:即,每个时刻,实际高度不得高于多少。
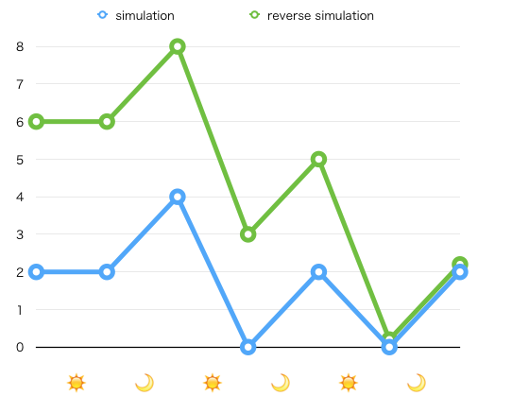
于是,通过时光倒流,问题转化为:每个竹子初始高度为\(\text{mid}\),每天高度会减少\(a_i\),我们每用一次砍伐机会可以使其高度增加\(p\)。在\(m\)天中要保证所有竹子高度始终非负,且\(m\)天结束后每个竹子高度要\(\geq h_i\)。
这样转化的好处是,我们避免了在正向时间中,一次砍伐减少的高度不足\(p\)的问题;转化后,每次砍伐操作一定能使当前竹子高度增加\(p\),与初始高度无关。
转化后,这是经典的贪心问题(CF1132D Stressful Training)。我们计算出每个竹子,在不被砍伐的情况下,每天减少\(a_i\)米,最多能坚持几天。以这个天数作为关键字,把所有坚持不足\(m\)天的竹子扔进一个小根堆里。依次完成\(k\cdot m\)次砍伐,每次取出堆顶。如果当前砍伐所在的天数已经大于堆顶能坚持的天数,则直接\(\texttt{return false}\),把\(\text{mid}\)调大。否则,对堆顶砍一刀(使其高度增加\(p\))。如果高度增加后,它能坚持到\(m\)天之后,就不用再放进堆里了;否则更新它能坚持到的天数,然后放回堆中。
最后,用剩余的砍伐次数,尝试把所有竹子补到\(h_i\)即可。
时间复杂度\(O((n+k\cdot m)\cdot \log n\cdot \log\inf)\)。其中\(\log n\)来自堆,\(\log\inf\)来自二分答案,这里取\(\inf=\max(h_i+m\cdot a_i)\leq5001\cdot 10^9\)。
参考代码:
//problem:CF506C
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
const int MAXN=1e5,MAXM=5000,MAXA=1e9;
int n,m,K,P,h[MAXN+5],a[MAXN+5];
bool check(ll mid){
priority_queue<pll,vector<pll>,greater<pll> >q;//greater -> 小的在前
static ll c[MAXN+5];
for(int i=1;i<=n;++i){
c[i]=mid;
if(mid-(ll)m*a[i]<0){
q.push(mk(mid/a[i],i));//(最多能维持多少天, 编号)
}
}
int cnt=0;
while(cnt<=K*m){
if(q.empty())break;
pll t=q.top();q.pop();
int d=cnt/K+1;
if(t.fi<d)return false;
c[t.se]+=P;
++cnt;
if(c[t.se]-(ll)m*a[t.se]<0){
q.push(mk(c[t.se]/a[t.se],t.se));
}
}
if(cnt>K*m)return false;
for(int i=1;i<=n;++i){
if(c[i]-(ll)m*a[i]>=h[i])continue;
ll gap=h[i]-(c[i]-(ll)m*a[i]);
ll need=gap/P+(gap%P!=0);
if(cnt+need>K*m)return false;
cnt+=need;
}
return true;
}
int main() {
cin>>n>>m>>K>>P;
ll l=0,r=(ll)(MAXM+1)*MAXA;
for(int i=1;i<=n;++i){
cin>>h[i]>>a[i];
l=max(l,(ll)a[i]);
}
while(l<r){
ll mid=(l+r)>>1;
if(check(mid))r=mid;
else l=mid+1;
}
cout<<l<<endl;
return 0;
}

