题解 CF1334 D,E,F,G Educational Codeforces Round 85 (Rated for Div. 2)
CF1334D Minimum Euler Cycle
构造题。
因为要求字典序最小,我们能贪则贪。
从\(1\)出发,依次走过:\(1-2-1-3-1-4-\dots -n\)。此时如果从\(n\)再走到\(1\),会发现所有从\(1\)出发的边都被使用过了,无法继续。所以不能走回\(1\)。我们走到\(2\),以\(2\)为中心,重复上述过程:\(2-3-2-4-2-\dots-n\)。这样,从\(2\)出发的所有边就都走过了。然后再走到\(3\),以\(3\)为中心,把所有从\(3\)出发的边走一遍,再回到\(n\)。以此类推,直到走完以\(n-1\)为中心,回到\(n\)后,最后一步从\(n\)走回\(1\)即可。
考虑求\([L,R]\)区间。我们可以依次枚举以每一个点为中心,记以当前点为中心时,会新经过的边数为\(cur\),这个值可以\(O(1)\)算出。用一个变量\(sum\)记录已经走过的总边数。如果\(sum+cur\geq L\),就暴力把以当前点为中心的\(cur\)条边依次走一遍,否则直接令\(sum\texttt{+=}cur\),继续考虑下一个中心点。当\(sum>R\)时,直接退出循环。
时间复杂度\(O(n+(R-L))\)。
参考代码:
const int MAXN=1e5;
int n,a[MAXN+5],ans[MAXN+5],cnt_ans;
ll L,R;
int main() {
int T;cin>>T;while(T--){
cin>>n>>L>>R;
int cnt=0;
a[++cnt]=1;
for(int i=n;i>1;--i){
a[++cnt]=i;
}
cnt_ans=0;
if(L==1)ans[++cnt_ans]=1;else L--;
R--;
ll sum=0;
if(L<=(n-1)*2-1){
ll c=1;
int v=2;
bool t=0;
while(1){
if(c>R||c>(n-1)*2-1)break;
if(t==0){
if(c>=L)ans[++cnt_ans]=v;
}
else{
if(c>=L)ans[++cnt_ans]=1;
v++;
}
++c;
t^=1;
}
}
sum+=(n-1)*2-1;
for(int i=2;i<n;++i){
if(sum+1>R)break;
if(sum+1>=L){
ans[++cnt_ans]=i;
}
sum++;
if(sum+1>R)break;
if(sum+(n-i)*2-1>=L){
ll c=sum+1;
int v=i+1;
bool t=0;
while(1){
if(c>R||c>sum+(n-i)*2-1)break;
if(t==0){
if(c>=L)ans[++cnt_ans]=v;
}
else{
if(c>=L)ans[++cnt_ans]=i;
v++;
}
++c;
t^=1;
}
}
sum+=(n-i)*2-1;
if(sum+1>R)break;
}
if(sum+1<=R){
ans[++cnt_ans]=1;
}
for(int i=1;i<=cnt_ans;++i)cout<<ans[i]<<" ";cout<<endl;
}
return 0;
}
CF1334E Divisor Paths
考虑一条边的边权是什么。我们设一条边为\((x,y)\),其中\(x>y\)且\(x\)是\(y\)的倍数。把\(y\)分解质因数。这\(y=p_1^{c_1}p_2^{c_2}\cdots p_k^{c_k}\)。设\(t=\frac{x}{y}\),\(t\)是一个质数。则边\((x,y)\)的边权为:\(\prod_{p_i\neq t}(c_i+1)\)。其含义是,我们要选择一个是\(x\)的约数而不是\(y\)的约数的数时,显然\(t\)的出现次数必须是\(t\)在\(x\)中的最高次(这样才能使得得到的数不是\(y\)的约数),且其他质因数的次数可以任选。
考虑从\(u\)走到\(v\)的最短路。
我们走的过程一定是,删掉一些质因子,再加入一些质因子——删掉在\(u\)中但不在\(v\)中的质因子,加入在\(v\)中但不在\(u\)中的质因子,对于既在\(u\)中也在\(v\)中的质因子,我们不用动。并且我们每一步只能改变一个质因子。
如何使边权和最小呢?显然,当我们对一个数操作时(不论是“加入”还是“删除”操作),它的质因子数量越少,边权就越少。所以在最短路中,我们一定是先做完所有删除操作,再做加入操作。
那么删除操作和加入操作内部应该按什么顺序进行呢?答案是任意顺序都可以!这一点我们用程序验证:随机一个数,把它的所有质因子拿出来,random_shuffle若干次,发现代价不变。当然,也可以用第一段中边权的公式证明。
于是,问题转化为,分别对\(u\), \(v\)分解质因数。以此确定哪些质因子是要删除的,哪些质因子是要加入的。
注意到一个优秀的性质:\(u\), \(v\)都是\(D\)的约数。我们可以预先在\(O(\sqrt{D})\)时间里对\(D\)分解质因子。然后,对\(u\)分解质因数时,只需要枚举\(D\)的每一个质因子,再枚举其次数。\(D\)的质因子种类不会超过\(O(\log D)\)种,每个质因子的次数不会超过\(O(\log D)\)。这种做法看上去是\(O(\log^2D)\)的,但其实是\(O(\log D)\)的,因为所有质因子的次数之和是\(O(\log D)\)的。
算方案数要预处理阶乘。预处理到质因子数量:也就是\(\log D\)即可。
时间复杂度\(O(\sqrt{D}+q\log D)\)。
参考代码:
/*
namespace Tester{
const int SIZE=1000000+5;
int c[SIZE],p[SIZE],cc[SIZE];
bool check(int x){
cout<<"check "<<x<<endl;
memset(c,0,sizeof(c));
int xx=x;
int cnt=0;
for(int i=2;i<=x;++i)if(x%i==0){
int _c=0;
while(x%i==0)x/=i,_c++,p[++cnt]=i;
c[i]=_c;
}
x=xx;
for(int i=2;i<=x;++i)cc[i]=c[i];
ll cost=0;
for(int i=1;i<=cnt;++i){
ll tmp=1;
for(int j=2;j<=x;++j)if(j!=p[i]){
tmp*=(c[j]+1);
}
cost+=tmp;c[p[i]]--;
}
cout<<"cost "<<cost<<endl;
int t=30;
while(t--){
for(int i=2;i<=x;++i)c[i]=cc[i];
random_shuffle(p+1,p+cnt+1);
ll tcost=0;
for(int i=1;i<=cnt;++i){
ll tmp=1;
for(int j=2;j<=x;++j)if(j!=p[i]){
tmp*=(c[j]+1);
}
tcost+=tmp;c[p[i]]--;
}
if(tcost!=cost)return 0;
//cout<<tcost<<endl;
}
return 1;
}
int main(){
srand((ull)time(0)^(ull)(new char));
while(1){
int x=(ll)rand()*rand()%1000000+1;
if(check(x))cout<<"YES"<<endl;
else {cout<<"NO"<<endl;return 0;}
}
}
}//namespace Tester
*/
const int MOD=998244353;
inline int pow_mod(int x,int i){int y=1;while(i){if(i&1)y=(ll)y*x%MOD;x=(ll)x*x%MOD;i>>=1;}return y;}
ll D,p[100];
int q,fac[100],ifac[100],cnt,cu[100],cv[100];
int main() {
fac[0]=1;
for(int i=1;i<=99;++i)fac[i]=(ll)fac[i-1]*i%MOD;
ifac[99]=pow_mod(fac[99],MOD-2);
for(int i=98;i>=0;--i)ifac[i]=(ll)ifac[i+1]*(i+1)%MOD;
cin>>D>>q;
ll x=D;
for(ll i=2;i*i<=x;++i)if(x%i==0){
p[++cnt]=i;while(x%i==0)x/=i;
}
if(x!=1)p[++cnt]=x;
while(q--){
ll u,v;
cin>>u>>v;
int sumdel=0,sumadd=0,invdel=1,invadd=1;
for(int i=1;i<=cnt;++i){
cu[i]=0;
x=u;while(x%p[i]==0)x/=p[i],cu[i]++;
cv[i]=0;
x=v;while(x%p[i]==0)x/=p[i],cv[i]++;
if(cu[i]<cv[i]){
sumadd+=cv[i]-cu[i];
invadd=(ll)invadd*ifac[cv[i]-cu[i]]%MOD;
}
if(cu[i]>cv[i]){
sumdel+=cu[i]-cv[i];
invdel=(ll)invdel*ifac[cu[i]-cv[i]]%MOD;
}
}
int res=(ll)fac[sumdel]*invdel%MOD*fac[sumadd]%MOD*invadd%MOD;
cout<<res<<endl;
}
return 0;
}
CF1334F Strange Function
设\(dp[i][j]\)表示考虑了\(a\)序列中的前\(i\)个数,下一位即将要匹配\(b\)序列中第\(j\)个数时的最小代价和。
转移有三种情况:
- 如果\(p_i<0\),则可以删掉\(p_i\),此时所有\(dp[i][j]=dp[i-1][j]+p_i\)。
- 如果\(p_i\geq0\),则\(p_i\)能不删就别删。设\(b\)序列里第一个\(b_x\geq a_i\)的位置为\(x\),则对于\(j\leq x\),令\(dp[i][j]=dp[i-1][j]+p_i\),对于\(x<j\leq m+1\),令\(dp[i][j]=dp[i-1][j]\)。
- 如果当前的\(a_i\)恰好是\(b\)序列中的某个数\(b_y\)。则\(dp[i][y+1]=\min(dp[i][y+1],dp[i-1][y])\)。
答案就是\(dp[n][m+1]\)。
DP数组的第二维,涉及到的操作是区间加、单点修改、单点求值。可以用线段树维护。
时间复杂度\(O(n\log m)\)。
参考代码:
const int MAXN=5e5;
const ll INF=1e18;
int n,a[MAXN+5],p[MAXN+5],m,b[MAXN+5];
struct SegmentTree{
ll val[MAXN*4+5],tag[MAXN*4+5];
void push_up(int p){
val[p]=min(val[p<<1],val[p<<1|1]);
}
void build(int p,int l,int r){
if(l==r){
if(l==1)val[p]=0;
else val[p]=INF;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
push_up(p);
}
void push_down(int p){
if(tag[p]){
val[p<<1]+=tag[p];
tag[p<<1]+=tag[p];
val[p<<1|1]+=tag[p];
tag[p<<1|1]+=tag[p];
tag[p]=0;
}
}
void range_add(int p,int l,int r,int ql,int qr,ll v){
if(ql<=l&&qr>=r){
val[p]+=v;
tag[p]+=v;
return;
}
push_down(p);
int mid=(l+r)>>1;
if(ql<=mid)range_add(p<<1,l,mid,ql,qr,v);
if(qr>mid)range_add(p<<1|1,mid+1,r,ql,qr,v);
push_up(p);
}
void point_ckmin(int p,int l,int r,int pos,ll v){
if(l==r){
val[p]=min(val[p],v);
return;
}
push_down(p);
int mid=(l+r)>>1;
if(pos<=mid)point_ckmin(p<<1,l,mid,pos,v);
else point_ckmin(p<<1|1,mid+1,r,pos,v);
push_up(p);
}
ll point_query(int p,int l,int r,int pos){
if(l==r)return val[p];
push_down(p);
int mid=(l+r)>>1;ll res=INF;
if(pos<=mid)res=point_query(p<<1,l,mid,pos);
else res=point_query(p<<1|1,mid+1,r,pos);
push_up(p);
return res;
}
}T;
int main() {
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i];
for(int i=1;i<=n;++i)cin>>p[i];
cin>>m;
for(int i=1;i<=m;++i)cin>>b[i];
T.build(1,1,m+1);
for(int i=1;i<=n;++i){
int x=lob(b+1,b+m+1,a[i])-b;
if(x==m+1){
T.range_add(1,1,m+1,1,m+1,p[i]);
}
else{
if(b[x]==a[i]){
ll v=T.point_query(1,1,m+1,x);
if(p[i]<0)T.range_add(1,1,m+1,1,m+1,p[i]);
else T.range_add(1,1,m+1,1,x,p[i]);
if(v<INF)T.point_ckmin(1,1,m+1,x+1,v);
}
else{
if(p[i]<0)T.range_add(1,1,m+1,1,m+1,p[i]);
else T.range_add(1,1,m+1,1,x,p[i]);
}
}
}
ll ans=T.point_query(1,1,m+1,m+1);
if(ans<=1000000000LL*n)cout<<"YES"<<endl<<ans<<endl;
else cout<<"NO"<<endl;
return 0;
}
CF1334G Substring Search
题外话:
在本题,以及许多与本题类似的字符串匹配问题中,如果\(|s|>|t|\),则显然不会有匹配。因此,我们只考虑\(|s|\leq|t|\)的情况。所以我们称\(s\)为短串,\(t\)为长串。这样就避免了“文本串”、“模式串”这种糟糕的翻译。
一个简单的想法是KMP。但是仔细考虑KMP算法的过程,发现它基于一个隐含条件:如果串\(a\)能匹配\(b\),串\(a\)能匹配\(c\),则串\(b\)也一定能匹配\(c\)(如下图)。但是这个隐含条件在本题中是不一定成立的。例如,如果\(p[a]=b\), \(a=c\)。无法就此推断出\(b=c\)或\(p[b]=c\)。
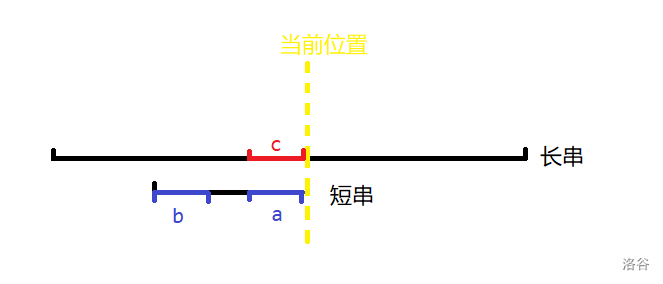
KMP行不通。我们考虑另一种常见的字符串匹配方法——FFT。
这里简单介绍一下用FFT做字符串匹配的原理。假设现在有两个串,短串为\(s\),长串为\(t\)(下标从\(0\)开始)。定义:\(s\)能在\(t\)的第\(i\)个位置匹配,当且仅当\(\forall j\in[0,m-1]\ s_{j}=t_{i-m+1+j}\)。考虑求出\(res_i=\sum_{j=0}^{m-1}(s_j-t_{i-m+1+j})\)。如果在第\(i\)个位置能够匹配,则\(res_i\)一定等于\(0\)。但是目前\(res_i=0\)还不是充分条件,因为有可能\((s_j-t_{i-m+1+j})\)的值有正有负,正好抵消。于是我们修改一下\(res\)的定义,重新定义\(res_i=\sum_{j=0}^{m-1}(s_j-t_{i-m+1+j})^2\),这样求和式中的所有项一定非负,所以此时:在第\(i\)个位置能够匹配,当且仅当\(res_i=0\)。
考虑如何快速求出所有\(res_i\)(\(i\geq m-1\))。我们把\(s\)翻转。则\(res_i=\sum_{j=0}^{m-1}(s_{m-j-1}-t_{i-m+1+j})^2\)。令\(j=m-j-1\),则\(res_{i}=\sum_{j=0}^{m-1}(s_j-t_{i-j})^2=\sum_{j=0}^{m-1}(s_j^2+s_jt_{i-j}+t_{i-j}^2)\)。第一项和第三项可以用前缀和简单求出,关键是求\(\sum_{j=0}^{m-1}s_jt_{i-j}\)。发现这个式子很像我们熟悉的FFT的形式:\(c_i=\sum_{j=0}^{i}a_jb_{i-j}\)。只不过\(j\)的上限现在是\(m-1\)而不是\(i\)。考虑对于所有\(i\geq m\),我们令\(s_i=0\)。则我们可以把枚举上限从\(m-1\)提高到\(i\)而不影响结果。于是直接做卷积就好了。
回到本题,我们多了一个\(p[s_i]=t_i\)这种匹配方式,且两种方式是“或”的关系。所有我们可以构造:\(res_i=\sum_{j=0}^{m-1}(s_j-t_{i-m+1+j})^2(p[s_j]-t_{i-m+1+j})^2\)。用和前面类似的方法,把\(s\)翻转,可得:\(res_i=\sum_{j=0}^{m-1}(s_j-t_{i-j})^2(p[s_j]-t_{i-j})^2\)。把这个式子大力展开,整理成关于\(t_{i-j}\)的多项式。可得:
可以发现这四项都是卷积的形式。做四次FFT即可。
为了避免精度误差,并且让写法更简便,可以用NTT代替FFT。但是,这么做(有极小的概率)可能会出现\(res_i\)的真实值不等于\(0\),但\(\bmod 998244353\)后等于\(0\)的情况。为了防止别人恶意构造这种情况来hack你,可以给每个字母随机一个权值,这样基本上就卡不掉了。但是要注意不同字母的权值一定要不同。
时间复杂度\(O(n\log n)\)。
参考代码:
//problem:CF1334G
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define mk make_pair
#define lob lower_bound
#define upb upper_bound
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
/* ------ by:duyi ------ */ // myt天下第一
const int MAXN=2e5,MOD=998244353;
inline int mod1(int x){return x<MOD?x:x-MOD;}
inline int mod2(int x){return x<0?x+MOD:x;}
inline void add(int &x,int y){x=mod1(x+y);}
inline void sub(int &x,int y){x=mod2(x-y);}
inline int pow_mod(int x,int i){int y=1;while(i){if(i&1)y=(ll)y*x%MOD;x=(ll)x*x%MOD;i>>=1;}return y;}
int p[26],val[26],m,n,s[MAXN+5],t[MAXN+5],vs[MAXN+5],vt[MAXN+5],res[MAXN+5],f[MAXN*4+5],g[MAXN*4+5],rev[MAXN*4+5];
char str[MAXN+5];
void NTT(int *a,int n,int flag){
for(int i=0;i<n;++i)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int i=1;i<n;i<<=1){
int T=pow_mod(3,(MOD-1)/(i<<1));
if(flag==-1) T=pow_mod(T,MOD-2);
for(int j=0;j<n;j+=(i<<1)){
for(int k=0,t=1;k<i;++k,t=(ll)t*T%MOD){
int Nx=a[j+k],Ny=(ll)a[i+j+k]*t%MOD;
a[j+k]=mod1(Nx+Ny);
a[i+j+k]=mod2(Nx-Ny);
}
}
}
if(flag==-1){
int invn=pow_mod(n,MOD-2);
for(int i=0;i<n;++i)a[i]=(ll)a[i]*invn%MOD;
}
}
bool ck(int i){
for(int j=0;j<i;++j)if(val[i]==val[j])return 0;
return 1;
}
int main() {
srand((ull)time(0)^(ull)(new char));
for(int i=0;i<26;++i){
val[i]=rand()%MOD;
while(!ck(i))add(val[i],1);
}
for(int i=0;i<26;++i)cin>>p[i],p[i]=val[p[i]-1];
cin>>str;m=strlen(str);reverse(str,str+m);
for(int i=0;i<m;++i)vs[i]=val[s[i]=str[i]-'a'];
cin>>str;n=strlen(str);//if(m>n){cout<<0<<endl;return 0;}
for(int i=0;i<n;++i)vt[i]=val[t[i]=str[i]-'a'];
int tmp=0;
for(int i=0;i<m;++i)add(tmp,(ll)p[s[i]]*p[s[i]]%MOD*vs[i]%MOD*vs[i]%MOD);
for(int i=m-1;i<n;++i)res[i]=tmp;
for(int i=0;i<m;++i)f[i]=(ll)p[s[i]]*vs[i]%MOD*mod1(p[s[i]]+vs[i])%MOD;
for(int i=0;i<n;++i)g[i]=vt[i];
int lim=1,ct=0;while(lim<=n+m)lim<<=1,++ct;
for(int i=0;i<lim;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(ct-1));
NTT(f,lim,1);NTT(g,lim,1);
for(int i=0;i<lim;++i)f[i]=(ll)f[i]*g[i]%MOD;
NTT(f,lim,-1);
for(int i=m-1;i<n;++i)sub(res[i],mod1(2*f[i]));
for(int i=0;i<m;++i)f[i]=((ll)vs[i]*vs[i]%MOD+(ll)p[s[i]]*p[s[i]]%MOD+4LL*vs[i]*p[s[i]]%MOD)%MOD;
for(int i=m;i<lim;++i)f[i]=0;
for(int i=0;i<n;++i)g[i]=(ll)vt[i]*vt[i]%MOD;
for(int i=n;i<lim;++i)g[i]=0;
NTT(f,lim,1);NTT(g,lim,1);
for(int i=0;i<lim;++i)f[i]=(ll)f[i]*g[i]%MOD;
NTT(f,lim,-1);
for(int i=m-1;i<n;++i)add(res[i],f[i]);
for(int i=0;i<m;++i)f[i]=mod1(vs[i]+p[s[i]]);
for(int i=m;i<lim;++i)f[i]=0;
for(int i=0;i<n;++i)g[i]=(ll)vt[i]*vt[i]%MOD*vt[i]%MOD;
for(int i=n;i<lim;++i)g[i]=0;
NTT(f,lim,1);NTT(g,lim,1);
for(int i=0;i<lim;++i)f[i]=(ll)f[i]*g[i]%MOD;
NTT(f,lim,-1);
for(int i=m-1;i<n;++i)sub(res[i],mod1(2*f[i]));
for(int i=0;i<m;++i)f[i]=1;
for(int i=m;i<lim;++i)f[i]=0;
for(int i=0;i<n;++i)g[i]=(ll)vt[i]*vt[i]%MOD*vt[i]%MOD*vt[i]%MOD;
for(int i=n;i<lim;++i)g[i]=0;
NTT(f,lim,1);NTT(g,lim,1);
for(int i=0;i<lim;++i)f[i]=(ll)f[i]*g[i]%MOD;
NTT(f,lim,-1);
for(int i=m-1;i<n;++i)add(res[i],f[i]);
for(int i=m-1;i<n;++i){
/*
for(int j=0;j<m;++j){
res[i]+=p[s[j]]*p[s[j]]*vs[j]*vs[j]-2*p[s[j]]*vs[j]*(p[s[j]]+s[j])*t[i-j]
+(vs[j]*vs[j]+p[s[j]]*p[s[j]]+4*vs[j]*p[s[j]])*t[i-j]*t[i-j]
-2*(vs[j]+p[s[j]])*t[i-j]*t[i-j]*t[i-j]+t[i-j]*t[i-j]*t[i-j]*t[i-j];
}
*/
if(!res[i])cout<<'1';else cout<<'0';
}
cout<<endl;
return 0;
}

