题解 CF1338 A,B,C,D Codeforces Round #633 (Div. 1)
CF1338A Powered Addition
我们知道,任何一个数,都能被唯一分解为若干个不同的\(2\)的次幂相加。那么,如果已知了所有操作结束后的结果序列\(b\),则答案就是\(\lfloor\log_2(\max_{i=1}^{n}b_i-a_i)\rfloor\)。
因此,我们就是要求出一个序列\(b\),满足\(b\)序列单调不降,且\(b_i\geq a_i\)。满足这两个条件的前提下,让\(\max_{i=1}^{n}(b_i-a_i)\)尽可能小。
直接令\(b_i\)等于\(a_{1\dots i}\)的前缀最大值即可。
时间复杂度\(O(n)\)。如果暴力计算\(\log_2\)的话复杂度多一个\(\log\)。
参考代码(片段):
const int MAXN=1e5,INF=1e9;
int n,a[MAXN+5];
int highbit(int x){
for(int i=30;i>=0;--i){
if((x>>i)&1)return i+1;
}
return 0;
}
int main() {
int T;cin>>T;while(T--){
cin>>n;
int premax=-INF,ans=0;
for(int i=1;i<=n;++i){
cin>>a[i];
premax=max(premax,a[i]);
ans=max(ans,highbit(premax-a[i]));
}
cout<<ans<<endl;
}
return 0;
}
CF1338B Edge Weight Assignment
初步转化
异或有一个重要的性质:同一个数异或两次会被抵消。由此可以得到一个推论:如果\(a\operatorname{XOR}b=0,b\operatorname{XOR}c=0\),则\(a\operatorname{XOR}c=0\)。
考虑三个叶子\(x\), \(y\), \(z\)。如果\(x\)到\(y\)的路径异或和为\(0\),且\(y\)到\(z\)的路径异或和为\(0\),则\(x\)到\(z\)的路径异或和也必为\(0\)。如下图。证明方法就是上面说的推论。
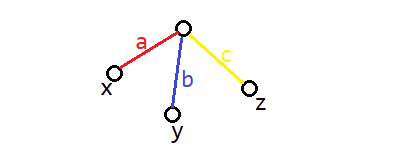
于是,问题可以从“所有叶子两两之间路径异或和为\(0\)”,转化为“某个叶子到其它所有叶子路径异或和都为\(0\)”。
任选一个度数为\(1\)的节点作为根。问题进一步转化为:求一种边权方案,使得根到每个叶子的路径异或和都为\(0\)。
求最小答案
定义\((\dots)_2\)表示二进制下的\(\dots\)这个数。
我们不妨先把所有边边权都设置为\(1\)。考虑在什么情况下,这么填会不合法。
我们定义一个节点的深度为它到根路径上的边数。发现当存在某个叶子节点深度为奇数时,这么填就是不合法的。在这种情况下如何改进呢?对于一个深度为奇数的叶子,当它和它父亲的边权为\((10)_2\),它父亲和它爷爷的边权为\((11)_2\)。容易发现,此时根到该叶子的路径异或和一定为\(0\)。
我们这么做了之后,可能会对其它叶子造成影响。具体来说:某个叶子到根的路径上可能会多出一些\((11)_2\)的边权。但是,我们总能通过把这个叶子和它父亲之间的边权,设置为\((01)_2\), \((10)_2\), \((11)_2\)之间的一种,使得它到根的路径异或和为\(0\)。
综上所述,最小答案只可能是\(1\)或\(3\)。且最小答案为\(1\)当且仅当所有叶子深度都为偶数。
求最大答案
初步的想法是,对于一条“连向非叶子节点”的边,令他的边权为\((1)_2\), \((10)_2\), \((100)_2\), \((1000)_2\), ......。对于“连向叶子节点”的边,令它的边权为,该叶子节点到根的路径(除它外)所有边边权的异或和。
这个思路基本上是对的,但是要注意两个小细节。
第一,对于同一个节点下面挂着的好几个叶子节点,它们的边权是一样的(注,“某某节点的边”指的是该节点与父亲之间的边,下同)。除此之外,任意两个叶子节点的边权都是不同的。
第二,对于深度为\(2\)的叶子节点,它的边权和它父亲一样。除此之外,每个叶子节点的边权在二进制下至少有两个\(1\),不会和任何一条连向非叶子节点的边边权相同。
时间复杂度\(O(n)\)。
参考代码(片段):
const int MAXN=1e5;
int n,cnt1,cnt2;
vector<int>G[MAXN+5];
bool have_odd_dep;
void dfs(int u,int fa,int dep){
int son_leave=0;
for(int i=0;i<SZ(G[u]);++i){
int v=G[u][i];
if(v==fa)continue;
dfs(v,u,dep+1);
if(SZ(G[v])==1)son_leave++;
else cnt1++;
}
if(fa&&SZ(G[u])==1){
//叶子
have_odd_dep|=(dep&1);
cnt2++;
}
if(son_leave>1){
cnt2-=(son_leave-1);
}
if(son_leave&&dep==1)cnt2--;
}
int main() {
cin>>n;
for(int i=1,u,v;i<n;++i)cin>>u>>v,G[u].pb(v),G[v].pb(u);
int root=0;
for(int i=1;i<=n;++i)if(SZ(G[i])==1){root=i;break;}
assert(root!=0);
dfs(root,0,0);
if(have_odd_dep)cout<<3<<" ";else cout<<1<<" ";
cout<<cnt1+cnt2<<endl;
return 0;
}
CF1338C Perfect Triples
找规律题。我们不妨先打个暴力,求出答案序列。同时,由于异或操作和二进制有关,所以顺便打出答案序列的二进制表示。
截取一些如下:
0000000001
0000000010
0000000011
0000000100
0000001000
0000001100
0000000101
0000001010
0000001111
0000000110
0000001011
0000001101
0000000111
0000001001
0000001110
0000010000
0000100000
0000110000
0000010001
0000100010
0000110011
0000010010
0000100011
0000110001
0000010011
0000100001
0000110010
0000010100
0000101000
0000111100
0000010101
0000101010
0000111111
0000010110
0000101011
0000111101
0000010111
0000101001
0000111110
...
因为题目的构造方式是三个一组,所以我们也把打出来的二进制数,按每三个一组分组。
不难发现:从第二组开始,每一组的后两位:以\((00,00,00),(01,10,11),(10,11,01),(11,01,10)\)四组为一周期循环。我们把循环中的这四个三元组,分别编号为\(0,1,2,3\)。直觉上容易想到:是对\(\frac{n}{3}\)做四进制分解(但实际上的规律比这个要略复杂)。为了验证我们的猜想,我们把组之间的关系写下来(以下每一行代表“一组”,即原序列里的三个元素):
0 0 0 1
0 0 1 0
0 0 1 1
0 0 1 2
0 0 1 3
0 1 0 0
0 1 0 1
0 1 0 2
0 1 0 3
0 1 1 0
0 1 1 1
0 1 1 2
0 1 1 3
0 1 2 0
...
发现,这并不是普通的四进制分解,因为这个序列的“最高位”永远是\(1\)。而最高位之后的数位,严格遵循了四进制分解的规则:满\(4\)进\(1\)。
因此,如果最高位为\(i\),则产生的组数是:\(4^{i-1}\)。我们把最高位相同的这些组,称为“一段”。通过枚举\(i\),我们可以在\(O(\log_4n)\)的时间里,确定\(n\)所在的组位于哪一段。
然后再把零头的部分做四进制分解即可。
时间复杂度\(O(T\log_4 n)\)。
参考代码(片段):
void print(int x){
for(int i=9;i>=0;--i)cout<<((x>>i)&1);cout<<endl;
}
const int a[4][3]={{0,0,0},{1,2,3},{2,3,1},{3,1,2}};
ull pw[100],s[100];
int sta[100],top;
int main(){
// static bool used[10000000];
// for(int i=1;i<=30;++i){
// int x=0,y=0,z=0;
// for(int i=1;i<=1000;++i)if(!used[i]){
// for(int j=i+1;j<=1000;++j)if(!used[j]){
// for(int k=j+1;k<=1000;++k)if(!used[k]&&(i^j^k)==0){
// x=i;y=j;z=k;break;
// }
// if(x)break;
// }
// if(x)break;
// }
// print(x);print(y);print(z);
// //cout<<x<<" "<<y<<" "<<z<<" ";
// used[x]=used[y]=used[z]=1;
// }
pw[0]=s[0]=1;for(int i=1;i<=30;++i)pw[i]=pw[i-1]*4,s[i]=s[i-1]+pw[i];
//cout<<pw[30]<<endl;
int T;cin>>T;while(T--){
ull n;cin>>n;
if(n<=3){
cout<<n<<endl;
continue;
}
--n;
ull b=n/3+1;
int h=0;
for(int i=0;i<=30;++i){
if(s[i]>=b){
h=i;break;
}
}
assert(h);
b-=s[h-1];
b--;
//cout<<"b "<<b<<endl;
top=0;
while(b){
sta[++top]=b%4;b/=4;
}
while(top<h){
sta[++top]=0;
}
int t=n%3;
ull res=a[1][t];
//cout<<"sta ";cout<<1<<" ";for(int i=top;i>=1;--i)cout<<sta[i]<<" ";cout<<endl;
//cout<<t<<endl;
for(int i=top;i>=1;--i){
res=(res<<2)+a[sta[i]][t];
}
cout<<res<<endl;
}
return 0;
}
CF1338D Nested Rubber Bands
图片引自wasa855的博客
考虑三个点的链,可以简单构造,如下图:
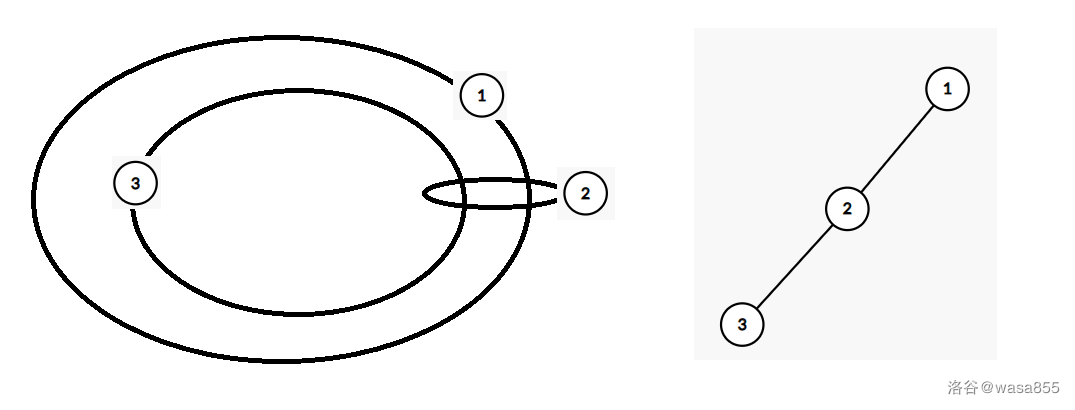
再考虑菊花的情况,也可以类似地构造,如下图:
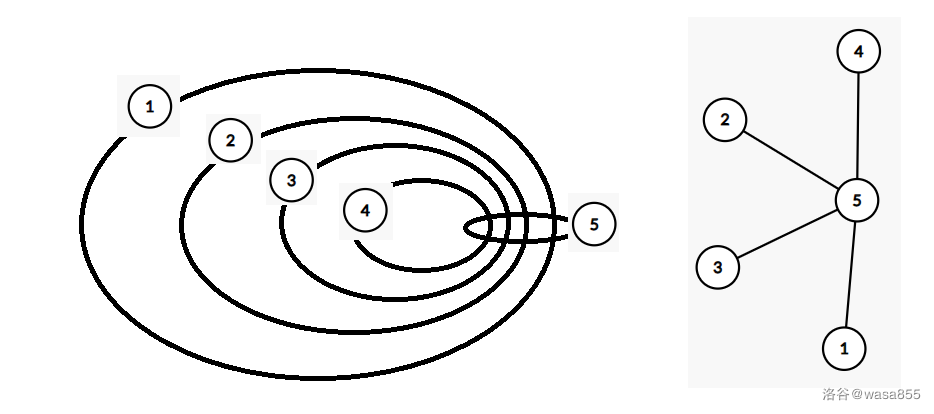
于是发现:与点\(u\)相邻的\(k\)个节点,可以被点\(u\)串成\(k\)层的圈。
不难想到,最终的构造方案中,一定是一部分点作为连通器,串起了若干个nested的圈。这些圈的数量就是答案了,因此我们希望被串起的圈越多越好。其他不对答案产生贡献的点,总能构造出一种摆放方法符合题意,所以求答案时可以不考虑它们。
如何让尽可能多的点,形成“一部分点作为连通器,串起了若干个nested的圈”这种结构呢?发现,能形成这个结构的点,充分必要条件是:树上的某一条链,以及所有与这条链距离为\(1\)的节点,共同组成的连通块。
另一个显然的性质是:树上两个相邻的节点,它们的圈不可能nested(否则就没有交了)。反过来,也可以说nested的点之间在树上一定没有边相连。
于是我们贪心地,在这个连通块内求最大独立集。把这个独立集作为nested的圈,连通块内其他点作为串起这些圈的连通器。
问题进一步转化为,对于树上所有链,考虑每条链所对应的连通块,求所有连通块的最大独立集的最大值。
可以做树形DP。设\(dp[u][0/1]\)表示考虑以节点\(u\)为一个端点,伸向\(u\)的子树内的链,最大独立集最大是多少。第二维\(0/1\)表示节点\(u\)是/否是独立集中的一个点(即:在答案的结构中,节点\(u\)是nested的圆圈还是圆圈间的连通器)。转移比较简单,可以看代码。
注意,不仅可以用每个节点的\(dp[u][0/1]\)更新答案,也要考虑一条“拐弯”的链。这样的链我们在LCA处更新答案。
时间复杂度\(O(n)\)。
参考代码(片段):
const int MAXN=1e5;
int n,dp[MAXN+5][2],ans;
vector<int>G[MAXN+5];
void dfs(int u,int fa){
dp[u][0]=1;
dp[u][1]=SZ(G[u])-(fa!=0);
for(int i=0;i<SZ(G[u]);++i){
int v=G[u][i];
if(v==fa)continue;
dfs(v,u);
ans=max(ans,dp[u][0]+dp[v][1]);
ans=max(ans,dp[u][1]-1+(fa!=0)+dp[v][0]);
ans=max(ans,dp[u][1]-1+(fa!=0)+dp[v][1]);
dp[u][0]=max(dp[u][0],dp[v][1]+1);
dp[u][1]=max(dp[u][1],dp[v][0]+SZ(G[u])-(fa!=0)-1);
dp[u][1]=max(dp[u][1],dp[v][1]+SZ(G[u])-(fa!=0)-1);
}
ans=max(ans,dp[u][0]);
ans=max(ans,dp[u][1]+(fa!=0));
}
int main() {
cin>>n;
for(int i=1,u,v;i<n;++i)cin>>u>>v,G[u].pb(v),G[v].pb(u);
dfs(1,0);
cout<<ans<<endl;
return 0;
}

